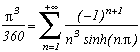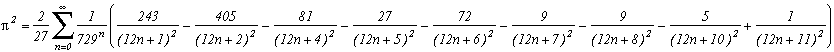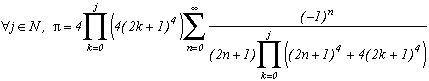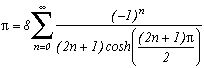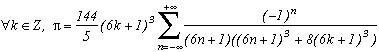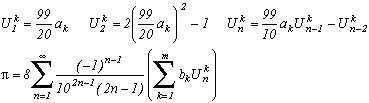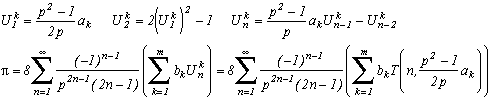Suites convergeant vers
Construites par des méthodes analytiques
(Par ordre chronologique des auteurs ou inspirateurs)

Autres fractions continues

Newton : (1642 - 1727)

   

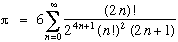
suite similaire :

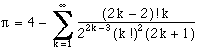
Leibniz (1646 - 1716)

Katahiro (1664 - 1739)

Machin (1680 - 1751)

Moivre/Stirling (1667 - 1754) / (1692 - 1770)

Euler (1707 - 1783)

1)
2)

3)

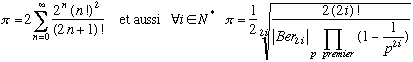
Buffon (1707 - 1788)

Si on lance une aiguille de longueur 2b sur un parquet formé de lames de largeur 2a, la probabilité pour que l'aiguille coupe l'une des raies de ce parquet est

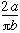
Gauss (1777 - 1855)

Cesaro (1859 - 1906)

La probabilité que deux entiers pris au hasard soient premier entre eux (pas de diviseur commun) est

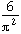
Ramanujan (1887 - 1920)

   



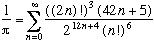
En notant (x)_n la valeur :
On peut écrire :

Gosper

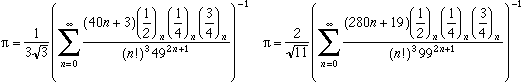
On a la formule générale pour x inférieur à 1 :

où ₂F₁ est une série hypergéométrique.

Pour x=1/2, on obtient :
qui connait une convergence en 2n
Pour on peut écrire :
de convergence 3,39n

Quelques formules bizarres où intervient Pi !






et en généralisant :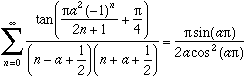

Sommes de Reynolds :

G et D.Chudnovsky

Borwein

avec A=63365028312971999585426220+28337702140800842046825600*5^1/2 + 384*5^1/2(10891728551171178200467436212395209160385656017 + 4870929086578810225077338534541688721351255040*5^1/2)^1/2
B=7849910453496627210289749000+3510586678260932028965606400 + 2515968*3110^1/2(6260208323789001636993322654444020882161 + 2799650273060444296577206890718825190235*5^1/2)^1/2
C=-214772995063512240-96049403338648032*5^1/2-1296*5^1/2(10985234579463550323713318473 + 4912746253692362754607395912*5^1/2)^1/2

Plouffe

Brown

Alors, prenons un entier naturel non nul n. Par exemple 10. Jusqu'ici tout va bien !
Considérons ensuite le plus proche multiple supérieur ou égal de n-1.
Dans notre cas, on trouve 18 car il est multiple de 9=10-1 et supérieur à 10.
Réitérons le procédé en considérant le plus proche multiple supérieur ou égal de n-2, ici 24, puis de n-3 (28), de n-4 (30) et ainsi de suite pour n-k jusqu'à ce que l'on arrive à k=n-1. On note f(n) le résultat (f(10)=34).
Eh bien, figurez-vous que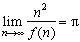

Woon

Bellard

avec

Mandelbrot/Bolle

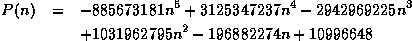
Considérons le point c=(-0.75,X) du plan complexe, c'est à dire un point à la verticale du cou de l'ensemble de Mandelbrot (le goulot d'étranglement).
Soit n le nombre d'itérations à partir duquel la récurrence quadratique caractéristique de l'ensemble de Mandelbrot Z_n+1=Z_n²+c avec Z₀=0 diverge (Zn2). Avec X de plus en plus petit, on a :

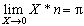
Théorème des résidus - E. Estenave - C. Frétigny

Je ne peux toutes les mettre, il y en a trop ! Vous les découvrirez au fil de la lecture de la page. Voici néanmoins quelques exemples :

mais aussi :



...

Anonymes (voir le grenier)

D' après les sommes de Riemann

         

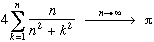
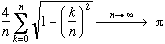
Triangle des c(n,k)

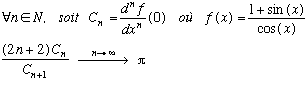
Quelques suites factorielles (voir Gosper)

(1) provient d'Euler et (2) de Comtet (1974)

Capes 1994

Soit D le disque de centre z₀ et rayon r :
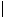
D(z₀,r)={zC z-z₀r}
et r_k=min{r>0, z₀C, card(Z[i]D(z₀,r))k}

alors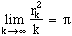

Polynômes de Chebyshev

Un premier exemple :


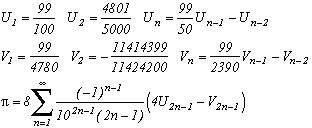
Si l'on connaît une relation du type :

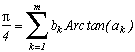
alors on peut construire les suites U_n^k et la série suivante :
Vous voulez autre chose que le 10 au dénominateur ? Soit, voici une formule encore plus générale pour p²>1, toujours en partant de la relation avec les Arctan :

avec T(n,x) le polynôme de Chebyshev.