William Gosper

On a la formule générale pour x inférieur à 1 :

où ₂F₁ est une série hypergéométrique, qui nous éloigne un peu de notre sujet, je n'en parlerai donc pas...

Pour x=1/2, on obtient :
qui connait une convergence en 2n
Pour on peut écrire :
de convergence 3.39n

William Gosper est aussi un habitué des formules un peu bizarres faisant intervenir , ne me demandez pas leur intérêt !
Par exemple :






et en généralisant :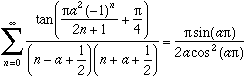

Tranches de vie

William Gosper fait partie des passionnés de Pi et du petit groupe d'irréductibles qui font souffrir les ordinateurs ! Gosper avait en effet déjà calculé 17,001,303 de termes de la fraction continue de Pi en 1977. Et il a ensuite programmé la série de Ramanujan (celle avec 1103) pour obtenir 17 millions de décimales. On ne savait pas alors si cette série convergeait, mais le calcul était juste et seul le nombre 1103 n'était pas justifié. Alors, comme le disent les Borwein, de même que deux entiers différent de moins d'une unité doivent être égaux, le nombre 1103 de trouvait vérifié. Car tout autre nombre aurait débouché sur des décimales parfaitement fausses à cause de la sensibilité aux erreurs...
Eh oui, aujourd'hui, on doit parfois se contenter de preuves empiriques !
N'enlevons rien néanmoins à la force scientifique de William Gosper, travaillant sur l'intelligence artificielle, et sur un petit paquet de propriétés concernant les séries factorielles convergeant vers Pi avec R. Schroeppel. D'où celle du dessus d'ailleurs dont je n'ai pas la démonstration malheureusement, mais qui doit ressembler à la démo ci-dessous.
Je ne sais pas non plus si c'est lui avec Schroeppel qui a trouvé :

=

ce qui me paraît bizarre compte tenu de la relative simplicité de la suite et de la preuve !

Autour de

En premier lieu, notons que la série factorielle du haut de la page serait parfaite pour un algorithme compte-goutte donnant Pi, sujet que je développerai prochainement sur une nouvelle page.
Mais puisque l'on parle d'un spécialiste des factorielles, profitons en pour aborder les autres séries factorielles tournant autour de Pi !
On notera pour plus de simplicité...
On a ainsi :



La formule (1) provient du grand Euler tandis que la (2) provient de Comtet en 1974.
La similitude de ces deux suites avec la somme des inverses de puissance est assez frappante...



Et bien sûr, il n'existe pas de resultat pour les puissances impaires !

Démonstration

La demonstration des séries factorielles est une simple et même méthode, typique de classe prépa, que j'expose ici rapidement pour le cas de la formule :
=. C'est d'ailleurs le même procédé que j'ai utilisé pour retrouver la démonstration de la formule de Katahiro...

On considère ainsi .
Cette série entière a 4 pour rayon de convergence. En effet, si on note
donc le résultat est immédiat par le critère de D'Alembert.

Comme c'est une série entière on peut dériver sans problème, et on a donc :


La résolution de l'équa diff est classique, je ne m'étends pas dessus... On obtient comme solutions générales et particulières respectives :


On en déduit le premier résultat .

Puis on dérive f et on obtient :


ce qui clot la démonstration...

Ainsi, pour obtenir la formule générale :
, on pourra remarquer que les membres de droite et de gauche de la première égalité vérifient l'équation différentielle :

(1-x²)f'(x)-xf(x)=1 pour x<1

Essais

Toutes ces suites ont des convergences linéaires ou très proche du linéaire (genre a.n+b.Ln(n)) car les termes des séries décroissent en c^-n.
Vérifions donc cela !

	Suite de Gosper	Suite de la démo	Suite (2) Comtet
n=5	3,14159249 (6)	3,1306 (1)	3,1415911 (5)
n=10	12 décimales exactes	3,14157 (4)	3,14159265340 (9)
n=50	57 décimales exactes	28 décimales exactes	35 décimales exactes
n=100	?	58 décimales exactes	66 décimales exactes

Plutôt concluant, non ?
La suite de Gosper a une convergence d'environ 1,2n, assez bien, pour ce genre de suites !
La suite de la démonstration s'en sort avec un 0,58n et la suite de Comtet (2) avec un 0,66n.
Tout cela est on ne peut plus correct !

Accélération de la convergence

Comme d'hab avec les suites à convergence linéaire, le Delta2 d'Aitken se veut efficace, mais beaucoup moins que l'on aurait pu espérer :

	Suite de Gosper	Suite de la démo	Suite (2) Comtet
n=5	3,1415926507 (8)	3,14195 (3)	3,1415924 (6)
n=10	14 décimales exactes	3,14159277 (6)	11 décimales justes
n=50	61 décimales exactes	31 décimales exactes	38 décimales exactes
n=100	?	62 décimales exactes	69 décimales exactes

3-4 décimales en plus, ce n'est pas terrible, donc contentons nous de pousser les séries un ou deux crans plus loin !