Pi et les fractales
Ensemble de Mandelbrot - Dave Boll - Gerald Edgar

Considérons le point c=(-0.75,X) du plan complexe, c'est à dire un point à la verticale du cou de l'ensemble de Mandelbrot (le goulot d'étranglement).
Soit n le nombre d'itérations à partir duquel la récurrence quadratique caractéristique de l'ensemble de Mandelbrot Z_n+1=Z_n²+c avec Z₀=0 diverge (Zn2). Avec X de plus en plus petit, on a :

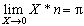
Mais quel rapport entre Pi et ce fameux ensemble de Mandelbrot ?

Ce joli dessin en haut de la page est l'ensemble de Mandelbrot (qui est connexe, en passant). Il est composé des points c=x+i*y du plan complexe (de coordonnées (x,y) dans le plan cartésien) tels que la suite Z_n+1=Z_n²+c avec Z₀=0 ne diverge pas. Dans la pratique pour construire cet ensemble et sa représentation graphique, on montre que lorsque le module de Z_n dépasse 2, il va diverger. Inutile d'attendre une grande valeur ! Les points c de l'ensemble de Mandelbrot sont alors représentés en noir (donc ceux pour lesquels Z_n reste bornée), et les couleurs différentes autour représentent les points selon la valeur de n à partir de laquelle on considère que la suite diverge.
En 1991, David Bolle tentait de vérifier si le rétrécissement que l'on observe en (-0.75,0) était bien infiniment étroit. C'est à dire que quelque soit l'épaisseur non nulle d'une ligne verticale que l'on ferait passer à cet endroit, elle rencontrerait la fractale avant la droite des abscisses.
Et D. Bolle eut donc l'idée d'utiliser le point c=(-0.75,X) pour l'itération quadratique et de faire tendre X vers 0. Et là, quel ne fut pas son étonnement en comptant le nombre d'itérations à partir duquel la suite divergeait, et en découvrant le tableau suivant :

X	Nbre d'itérations
1.0	3
0.1	33
0.01	315
0.001	3143
0.0001	31417
0.00001	314160
0.000001	3141593
0.0000001	31415928

Eh oui, c'était bien Pi qui apparaissait dans toute sa splendeur ! N'arrivant pas à démontrer le résultat, il le posta en 1992 sur le forum sci.math. Un certain Gerald Edgar d'une université de l'Ohio y répondit le 27 mars 1992 en apportant une explication intuitive de ce résultat, c'est ce qui est retranscrit plus bas dans la section "Tentative..."
Par la suite, D. Bolle approcha le problème avec un autre point, à savoir c=(0.25+X,0), c'est à dire le creux des... disons... fesses de l'ensemble (ils appellent cela plus poétiquement "butt" en anglais...), à droite.
Et là encore, même surprise, cette fois-ci, c'est X^1/2*n qui tend vers Pi :

X	Nbre d'itérations
1.0	2
0.1	8
0.01	30
0.001	97
0.0001	312
0.00001	991
0.000001	3140
0.0000001	9933
0.00000001	31414
0.000000001	99344
0.0000000001	314157

Quelques mots sur Mandelbrot, l'inspirateur !

Benoît Mandelbrot est né en Pologne en 1924 et émigre en France en 1936 avec sa famille, dont Szolem Mandelbrojt, mathématicien et professeur au collège de France.
Très vite, Benoît se révèle un esprit très éclectique et souvent en déphase avec les modes de pensées du moment. Son séjour à l'ENS Ulm est court (une journée !) et il rentre à Polytechnique en 1944. En opposition avec le climat Bourbakiste de l'école mathématique Française, il fera par la suite l'essentiel de sa carrière aux Etats-Unis (Maths appliquées et économie à Harvard, mais aussi sciences de l'ingénieur et physiologie à Yale et Einstein college of Medecine !).
Son oncle Szolem l'introduit en 1945 aux travaux oubliés de Gaston Julia (1918) sur les ensembles de points complexes issus d'itérations successives. Benoît préfère suivre sa propre voie, guidé par une intuition géométrique fabuleuse, mais retombe en fait dans les années 1970 sur les résultats des papiers de Julia. Il élabore alors la théorie des fractales dans "Les objets fractals, forme, hasard et dimension" (1975) et surtout "The fractal geometry of nature" (1982). Grâce aux laboratoires de recherche que lui met à disposition IBM, il inspire profondément la vision géométrique des fractales et développe les premiers programmes de création graphique sur ordinateurs.

Une tentative d'explication du phénomène

Elle est donc donnée par Gerald Edgar et il n'existe pas à ma connaissance (ou plutôt sur l'Internet !) de preuve rigoureuse du résultat. Edgar utilise le cas c=(0.25+X,0) :
On considère donc la suite Z_n+1=Z_n²+1/4+X, avec Z₀=0.
Celle-ci croit lentement vers 1/2 (la limite si X=0 d'après le théorème du point fixe) puis, passée ce seuil, diverge rapidement par la suite. Intéressons-nous donc au point 1/2 en décalant la suite, c'est à dire en posant Z_n=Y_n+1/2. Notre équation devient Y_n+1+1/2=(Y_n+1/2)²+1/4+X, soit :

Y₀=-1/2
Y_n+1=Y_n²+Y_n+X

Les Y_n croissent vers 0 doucement et lentement au voisinage inférieur de 0, donc on peut considérer que Y_n est en ce cas une fonction de n, pris comme variable continue, et - grosse astuce ! - on peut alors considérer que Y_n+1-Y_n est très proche de Y_n', la dérivée de Y_n
Donc notre équation devient : Y_n'=Y_n²+X soit :

Ah ah... On sait résoudre ce genre d'équations, cela donne :

Mais puisque l'on étudie Y_n lorsqu'il s'approche de 0, le dernier point de l'itération avant que Y_n s'échappe correspond donc au moment où tan s'approche négativement de 0, soit b=0 et a.n proche de soit :

où n est le nombre d'itérations avant que Y_n s'échappe, ce qui est exactement le résultat expérimental trouvé par D. Bolle.

C'est tout de même assez étonnant comme méthode de calcul de Pi. Imaginez que vous ne calculez plus itération après itération les décimales de Pi, mais qu'inversement ce sont les décimales de Pi qui vont vous donner la précision voulue sur X ! Si l'on imaginait que l'on puisse faire autant d'itérations que l'on veut en un temps raisonnable, cela aurait pu devenir un bon jeu : vous tentez de trouver quelle sera la prochaine décimale de Pi en calculant le nombre d'itérations que vous voulez grâce à votre prévision !

D'autres cas ?

Revenons tout d'abord au premier cas c=(-0.75,X). On utilise Z_n+1=f(Z_n)=Z_n²-3/4, de point fixe 1/2, de valeur propre -1, donc on utilise f(f(z)) et Z_n=-1/2+Y_n pour avoir Y_n proche de 0. Par le même processus que précédemment, on obtient l'équation différentielle :

L'intégrale qui en découle n'est pas simplement résoluble, mais on peut en déduire que le nombre d'itérations requis pour la divergence est asymptotique à /(2X). Puisque cela concerne la composition f(f(z)), il faut pour que cela diverge pour f(Z_n) le double, soit /X, ce qui confirme encore le résultat de D. Bolle pour ces points.

Un des bons principes de ce calcul avec l'ensemble de Mandelbrot est qu'un bon nombre de rétrécissements existent, on le voit graphiquement. Donc plusieurs angles d'attaque sont envisageables, comme les points (-1.25,X). Malheureusement, il y a pour ce cas un comportement un peu chaotique au début, et la mémoire de mon calculateur n'y a pas résisté ! David Petry, qui a fait le calcul, indique que n*X/ est toujours très proche d'un entier ou de la moitié d'un entier pour X petit. Ces angles d'attaque sont assez évidents car ils sont verticaux ou horizontaux, mais les multiples bourrelets peuvent donner lieu à d'autres relations intéressantes.

Mieux, on peut remplacer Z_n² par Z_n³ ou Z_n⁴, cela donne de nouveaux ensembles de Mandelbrot comme ci dessous, et voici de nouveaux rétrécissements en perspective ! Je ne connais par contre pas les points où l'on peut essayer, si quelqu'un peut me les fournir pour que je fasse des essais...

(Z_n³) (Z_n⁴)

Le vaste sujet des fractales et ensembles de Julia

Et si vous voulez approfondir la théorie des fractales, il n'existe pas grand chose en Français dessus, mais le répertoire de yahoo.com est assez fourni en revanche. Signalons également qu'il existe un bon nombre d'applets Java pour dessiner les ensembles de Julia et Mandelbrot, ces applets sont disséminées dans les sites consacrés aux fractales.
Cette théorie semble très à la mode aujourd'hui, surtout en France où les TIPE de prépa consacrés aux systèmes dynamiques pendant deux ans y ont largement fait référence.

Pour compléter l'ensemble de Mandelbrot et la théorie des points complexes obtenus par itérations, disons un tout petit mot des ensembles de Julia, qui sont intimement liés.

Ils proviennent d'un papier de Gaston Julia, éminent mathématicien Français de l'entre-deux guerres et professeur à Polytechnique. On reprend l'itération quadratique mais on fixe le point c cette fois-ci et c'est Z₀ que l'on va faire varier. Et l'on reprend les points pour lesquels Z_n est bornée à Z₀ variable pour construire l'ensemble de Julia. Il y a donc un ensemble de Julia pour chaque point c. Cela donne de nouvelles images et des propriétes assez profondes. Par exemple, si l'on prend un point de l'ensemble de Mandelbrot, l'ensembles de Julia associé est connexe, sinon, non. Voici quelques exemples :

Dendrite Fractale, c=(0,1)=i

DouadysRabbit Fractale c=(-0.123,0.745)=-0.123+0.745i

San Marco Fractale c=(-3/4,0)=-3/4