|
|
|
|
|

Salle Pi du palais de la découverte à Paris
Et pour quelques décimales de plus...
Histoire des records et méthodes
Depuis Archimède,
les mathématiciens ont tenté de calculer un maximum de décimales
du nombre Pi, même si cela paraît parfois une quête inutile
à certains... Mais sans ces efforts, on serait passé à
côté de beaucoup de découvertes de nouveaux algorithmes
et de méthodes de multiplication rapide mises au point ces dernières
années ! Pensez donc aux retombées des formules BBP de Plouffe
!
C'est donc bien une partie vivante et productive des mathématiques que
celle consiste à découvrir, optimiser et rendre encore plus rapide
tous les algorithmes de calcul.
Sommaire
Méthodes algorithmiques utilisées dans le calcul des décimales de Pi
Les meilleurs calculs de décimales de Pi à travers les âges...
Décimales calculées à la main puis sur des ordinateurs
Position calculée (digit en base 2 sans les digits précédents)
Fraction continue de Pi
Record de décimales dans une classe
Records de mémorisation
Les annonces de record
Les échos du record de Takahashi-Kanada datant d'avril 1999 (68 719 470 000 décimales)
Les échos du record de Kanada de septembre 1999 (206,158,430,000 décimales)
Les échos du record de Kanada datant de décembre 2002 (1 241 100 000 décimales)
Statistiques sur Pi
1 000 000 de décimales de Pi
Méthodes algorithmiques utilisées dans le calcul des décimales de Pi
- Delta2 d'Aitken
Une méthode d'accélération optimale de la convergence des suites à comportement géométrique
- Algorithme de Newton
- Atteindre le n-ième digit d'un nombre sans connaître les précédents (méthode de Simon Plouffe)
- Multiplication de deux grands entiers par Transformée de Fourier Rapide
Les meilleurs calculs de décimales de Pi à travers les âges...
(en notations modernes, bien sûr...)
note : 4*2+4*3 veut dire Pi=4 arctan(1/2)+4arctan(1/3), c'est la formule qui sert à calculer les décimales (au moyen du DL d'arctan)
| NOM |
DATE |
Approx. ou méthode utilisée |
Décimales justes |
| Babyloniens |
-2000 |
3+1/8=3,125 |
1 |
| Egyptiens (scribe Ahmès) |
-1650 |
(16/9)2=3,16045 |
1 |
| Chinois |
-1200 |
3 |
0 |
| Bible |
-550 |
3 |
0 |
| Archimède |
-250 |
3,14185 |
3 |
| Hon Han Shu |
130 |
1 |
|
| Ptolémée |
150 |
377/120=3,14166 |
3 |
| Chung Hing |
250 |
1 |
|
| Wang Fau |
250 |
142/45=3,155 |
1 |
| Liu Hui |
264 |
3,14159 |
5 |
| Siddhanta |
380 |
3+177/1250=3,1416 |
3 |
| Tsu Chung Chih |
480? |
355/113=3,141592 |
6 |
| Aryabhata |
499 |
3,14156 |
4 |
| Brahmagupta |
640 |
101/2=3,1622 |
1 |
| Al-Khowarizmi |
800 |
3,1416 |
3 |
| Fibonacci |
1220 |
3,141818 |
3 |
| Al-Kashi |
1429 |
6016I59II28III1IV34V51VI46VII14VIII50IX |
14 |
| Otho |
1573 |
3,1415929 |
6 |
| Viete |
1593 |
3,1415926536 |
9 |
| Romanus |
1593 |
|
15 |
| Van Ceulen |
1596 |
méthode d' Archimède |
20 |
| Van Ceulen |
1609 |
" |
34 |
| Grienberger |
1630 |
" |
39 |
| Newton |
1665 |
" |
16 |
| Sharp |
1699 |
" |
71 |
| Seki |
1700 |
" |
10 |
| Machin |
1706 |
16*5-5*239 (Machin) |
100 |
| De Lagny |
1719 |
4*2+4*3 (Euler) |
112 (sur 127 calculées) |
| Takebe Katahiro |
1723 |
polygone 1024 côtés |
41 |
| Matsunaga |
1739 |
|
50 |
| Vega |
1794 |
20*7+8arctan(3/79) (Euler 1755) |
140 |
| Rutherford |
1824 |
16*5-4*70+4*99 |
152 (sur 208) |
| Strassnitsky, Dahse |
1844 |
4*2+4*5+4*8 |
200 |
| Clausen |
1847 |
8*3+4*7 (Hutton 1776) |
248 |
| Lehmann |
1853 |
8*3+4*7 |
261 |
| Rutherford |
1853 |
formule de Machin |
440 |
| Shanks |
1874 |
formule de Machin |
527 (sur 707) |
| Ferguson |
1945 |
12*4+4*20+4*1985 |
539 |
| Ferguson |
1947 |
|
620 |
| Ferguson |
1948 |
|
710 |
| Ferguson et wrench |
1948 |
|
808 |
| Smith et Wrench |
1949 |
|
1 120 |
| Reitwiesner sur l' ENIAC |
1949 |
formule de Machin |
2 037 |
| Nicholson et Jeenel |
1954 |
formules d'arctan |
3 092 |
| Felton |
1957 |
32*10-4*239-16*515 |
7 480 |
| Genuys |
01-1958 |
|
10 000 |
| Felton |
05-1958 |
48*18+32*57-20*239 |
10 021 |
| Guilloud |
1959 |
|
16 157 |
| Shanks et Wrench |
1961 |
24*8+8*57+4*239 |
100 265 |
| Guilloud et Filliatre |
1966 |
|
250 000 |
| Guilloud et Dichampt |
1967 |
|
500 000 |
| Guilloud et Bouyer |
1973 |
formules Störmer+ Gauss |
1 001 250 |
| Miyoshi et Kanada |
1981 |
|
2 000 036 |
| Guilloud |
1982 |
|
2 000 050 |
| Tamura |
1982 |
|
8 388 576 |
| Kanada, Yoshino et Tamura |
1982 |
|
16 777 206 |
| Gosper |
1985 |
suite de Ramanujan |
17 526 200 |
| Bailey |
01-1986 |
algorithmes d' ordre 2+ d' ordre 4 des Borwein |
29 360 111 |
| Kanada et Tamura |
10-1986 |
algo d 'ordre 2 et 4 des Borwein |
67 108 839 |
| Kanada, Tamura, Kobo |
01-1987 |
" |
134 217 700 |
| Kanada et Tamura |
01-1988 |
" |
201 326 551 |
| Chudnovsky et Chudnovsky |
05-1989 |
Suites de type Ramanujan |
480 000 000 |
| Chudnovsky et Chudnovsky |
06-1989 |
Suites de type Ramanujan |
525 229 270 |
| Kanada et Tamura |
07-1989 |
algo d 'ordre 2 et 4 des Borwein |
536 870 898 |
| Chudnovsky et Chudnovsky |
08-1989 |
Suites de type Ramanujan |
1 011 196 691 |
| Kanada et Tamura |
11-1989 |
algo d 'ordre 2 et 4 des Borwein |
1 073 741 799 |
| Chudnovsky et Chudnovsky |
08-1991 |
Suites de type Ramanujan |
2 260 000 000 |
| Chudnovsky et Chudnovsky |
05-1994 |
Suites de type Ramanujan |
4 044 000 000 |
| Kanada |
06-1995 |
algo d 'ordre 2 et 4 des Borwein |
4 294 967 286 |
| Kanada |
10-1995 |
algo d 'ordre 2 et 4 des Borwein |
6 442 450 938 |
| Takahashi-Kanada |
08-1997 |
algo d 'ordre 2 et 4 des Borwein |
51,539,600,000 |
| Takahashi-Kanada | 04-1999 |
algo de Brent/Salamin |
68,719,470,000 |
| Takahashi-Kanada | 20-09-1999 | 206,158,430,000 soit environ 3.236 |
|
| Kanada | 06-12-2002 | formules type Machin 48*49+128*57-20*239+48*110443 176*57+28*239-48*682+96*12943 |
1,241,100,000,000 |
d'après D. Bailey, J. et P. Borwein, S. Plouffe et moi-même
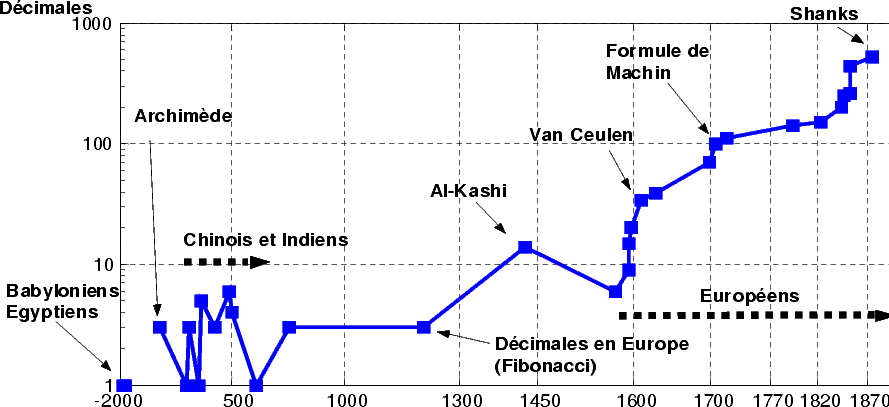
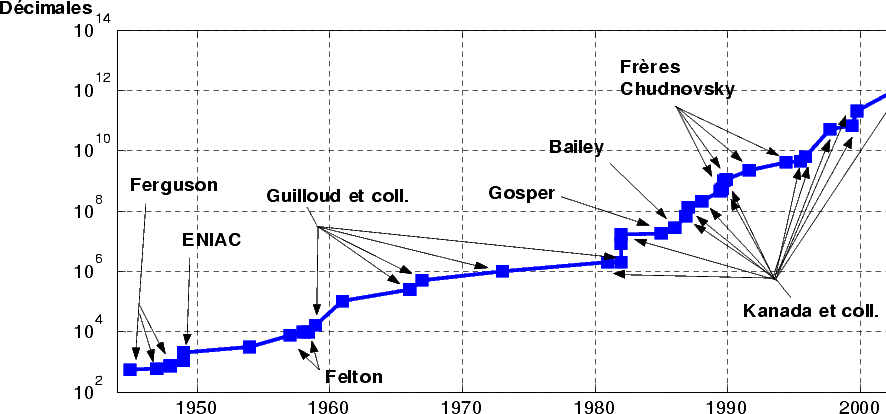
Décimales calculées à la main puis sur des ordinateurs
D'autres graphiques (personnels)
Position calculée (digit en base 2 sans les digits précédents)
| Bailey-Borwein-Plouffe |
1996 |
40 000 000 000 |
| Bellard |
6-7-1996 |
50 000 000 000 |
| Bellard |
7-10-96 |
100 000 000 000 |
| Bellard |
22-9-97 |
1 000 000 000 000 |
| Colin Percival - Project Pihex |
21-8-98 |
5 000 000 000 000 |
| Colin Percival - Project Pihex |
9-2-99 |
40 000 000 000 000 |
| Colin Percival - Project Pihex | 11-09-2000 |
1 000 000 000 000 000 |
Fraction continue de Pi
Pas mal de termes de la fraction continue de Pi ont été calculés. Voici les principaux records en date :
| Gosper |
1977 |
17,001,303 |
| H. Havermann |
Juin 1999 |
20,000,000 |
| H. Havermann | Mars 2002 |
180,000,000 |
Notez qu'Havermann présente une très intéressante page explicative à propos de la fraction continue de Pi
Record de décimales dans une classe
Bon, d'accord, c'est un record que j'ai inventé ;-)... mais c'est pour rendre hommage à la classe de 5ème Berlin du collège de Bouchain (59111) dans le département du Nord en France, qui se réunit tous les lundi afin de rajouter quelques décimales à son mur de classe ! Ils en sont à 85 en cette année 2012/2013 ! Bravo à eux !! (cliquez sur les images pour avoir les grands formats)
Records de mémorisation
Un japonais détient le record, essayez d'imaginer ce que cela représente en termes de mémoire, c'est fou !
Les principaux records :
| Simon Plouffe |
1975 |
4096 |
| Hideaki Tomoyori |
1979 |
15,151 |
| Hiroyuki Goto (en 9h) |
1995 |
42,000 |
| Akira Haraguchi (détails ci-dessous) | 2006 |
100,000 |
 Akira Haraguchi, un Japonais de 60 ans, a récité 100 000 décimales de Pi en 16h30 le 3 octobre 2006, battant ainsi son propre record (non-officiel) de 83 431 décimales établi l'année dernière ! Premier commentaire de l'intéressé: "Je n'ai rien ressenti de sensationnel, j'ai juste vidé tout ce qu'il y avait dans ma mémoire" ;-) Voir ici la dépêche AFP, là le classement des records de mémorisation (non mis à jour) et de ce côté la dépêche sur son précédent record de 2005.
Akira Haraguchi, un Japonais de 60 ans, a récité 100 000 décimales de Pi en 16h30 le 3 octobre 2006, battant ainsi son propre record (non-officiel) de 83 431 décimales établi l'année dernière ! Premier commentaire de l'intéressé: "Je n'ai rien ressenti de sensationnel, j'ai juste vidé tout ce qu'il y avait dans ma mémoire" ;-) Voir ici la dépêche AFP, là le classement des records de mémorisation (non mis à jour) et de ce côté la dépêche sur son précédent record de 2005.
1000 milliardième (10^12) digit binaire de PI par Fabrice Bellard- 22/09/97
5 000 milliardième digit de Pi est '0' par Colin Percival (projet PiHex) - 21/08/98
40 000 milliardième digit de Pi est '0' par Colin Percival (projet PiHex) - 9/02/99
Le millionième de milliards digit binaire de Pi (1015) est '0' par Colin Percival (projet PiHex) - 11/09/00
51,539,600,000 décimales de Pi par Kanada
08/06/97
206,158,430,208 (=3*2^36) décimales de Pi par Kanada
04/10/99
Les échos du record de Takahashi-Kanada datant d'avril 1999 (68 719 470 000 décimales)
Deux calculs sur un HITACHI SR8000 basés sur deux algorithmes indépendants (méthode de Brent/Salamin et algorithme d'ordre 4 des frêres Borwein) ont généré 68,719,476,736 (=236) décimales de Pi. En comparant les deux résultats, on a trouvé 68,719,476,693 décimales communes. Le nouveau record mondial a donc été proclamé pour 68,719,470,000 décimales de Pi calculées.
Programme principal :
Début : 2 Avril 1999 20:14:38
Fin : 4 Avril 1999 05:08:41
Temps total : 32:54:02
Mémoire utilisée : 296 GB
Algorithme : Gauss-Legendre (Brent-Salamin)
Programme de vérification :
Début : 4th April 1999 05:08:48
Fin : 5th April 1999 20:29:25
Temps total : 39:20:37
Mémoire utilisée : 280 GB
Algorithme : ordre 4 des Borwein
Les échos du record de Kanada de septembre 1999 (206,158,430,000 décimales)
Deux calculs sur un HITACHI SR8000 basés sur deux algorithmes indépendants (méthode de Brent/Salamin et algorithme d'ordre 4 des frêres Borwein) ont généré 206,158,430,208 (=3.2^36) décimales de Pi. En comparant les deux résultats, on a trouvé 206,158,430,163 décimales communes. Le nouveau record mondial a donc été proclamé pour 206,158,430,000 décimales de Pi calculées.
Programme principal :
Début : 18 Septembre 1999 19:00:52 (heure du Japon)
Fin : 20 Septembre 1999 08:21:56
Temps total : 37:21:04
Mémoire utilisée : 865 GB (=6.758*128)
Algorithme : Gauss-Legendre (Brent-Salamin)
Programme de vérification :
Début : 26 Juin 1999 01:22:50
Fin : 27 Juin 1999 23:30:40
Temps total : 46:07:10
Mémoire utilisée : 817 GB (=6,383*128)
Algorithme : ordre 4 des Borwein
Les échos du record de Kanada datant de décembre 2002 (1 241 100 000 000 décimales)
Deux calculs pendant près de 600 heures sur un HITACHI SR8000/MP doté de 1TB de stockage (1024Go), et basés sur deux formules indépendantes de type Machin, ont généré 1,241,100,000 décimales de Pi après que le résultat obtenu en base hexadécimale ait été converti en base dix. Les formules employées sont :
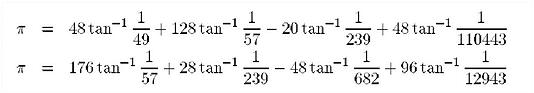
Ce retour à des formules étonnament simples après l'utilisation pendant une quinzaine d'années des algorithmes de Brent-Salamin, des Borwein ou des séries de Ramanujan et Chudnovsky était vraiment inattendu. il semble que malgré les améliorations algorithmiques perpétuelles, la complexité de ces formules avait atteint la limite des capacités des ordinateurs. En effet, l'utilisation perpétuelle de racines, multiplications et divisions nécessitait l'utilisation de la transformée de fourier rapide (FFT) à très grande échelle. Cette dernière requiert énormément de mémoire pour fonctionner. Kanada est donc revenu à des méthodes plus sages, qui nécessitent sensiblement plus d'opérations arithmétiques mais ne requièrent pas de très larges FFT et donc beaucoup moins de mémoire. Ces difficultés sont récemment apparues même au niveau des plus gros ordinateurs de la planète, dont les communications réseau et mémoire semblaient finir par saturer plus vite que la théorie ne le prévoyait. Kanada estime que son implémentation est environ deux fois plusplus rapide que la précédente qui utilisait l'algorithme des Brent-Salamin et celui d'ordre quartique des Borwein.
Quelques articles ou sites sélectionnés à consulter à propos de ce record :
Le Laboratoire de Kanada avec de nombreux articles dans "Press Release"
Page de J. Borwein consacrée au record
MathTrek (Ivan Peterson)
Statistiques sur Pi
Fréquence de distribution des décimales sur les 50 000 000 000 premières:
'0' : 5000012647
'1' : 4999986263
'2' : 5000020237
'3' : 4999914405
'4' : 5000023598
'5' : 4999991499
'6' : 4999928368
'7' : 5000014860
'8' : 5000117637
'9' : 4999990486
Chi deux = 5.60
Fréquence de distribution des décimales de 1/Pi sur les 50,000,000,000 premières:
'0' : 4999969955
'1' : 5000113699
'2' : 4999987893
'3' : 5000040906
'4' : 4999985863
'5' : 4999977583
'6' : 4999990916
'7' : 4999985552
'8' : 4999881183
'9' : 5000066450
Chi deux = 7.04
Sur cette page, vous avez aussi le moyen de récupérer un million de décimales !
- Visualiser
(HTML) (1.1 Mo)
- Télécharger (stuffit) (488Ko)
- Télécharger (zip) (528Ko)
Mais si vous en
voulez encore plus....
- Récupérer 4 200 000 000 décimales (4 milliards 200 millions)
Les 1000 premières pour s'amuser....
3,1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679
8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196
4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273
7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094
3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912
9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132
0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235
4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859
5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303
5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989...
retour à la page d' accueil






