|
|
|
|
|
LE GRENIER
SUITES ORIGINALES ET INEFFICACES...
Quelques suites totalement inefficaces...
Par la méthode des sommes de Riemann :
(1)
(2)(3) 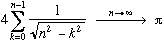
Petite suite perso trouvée par mon pote David et moi
(elle se construit en considérant un cercle où l'on inscrit des trapèzes verticaux. En calculant l'aire de ces trapèzes d'une certaine manière, on tombe sur la suite que voilà !)
Suite isolée !
c'est une suite archimédienne (polygones dans un cercle), démonstration prochainement !
Statistique/dénombrement
1) voir Cesàro
2) Triangle des c(n,k)
3) Application de la loi des grands nombres
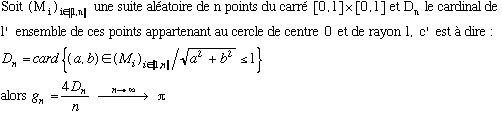
Un peu de géométrie
Le volume d'une boule dans Rn est donné par la formule :
où n=2m. Remarquons que cela marche bien pour m=1, n=2 mais en plus cela marche aussi pour n impair! En effet, pour n=1, la longueur du segment est 2R donc :
Et ce n'est pas du pipeau ! Rappelons nous en effet que la fonctiond'Euler vérifie pour n entier
(n)=(n-1)! et plus généralement pour x réel positif,
(x)=(x-1)
(x-1)
Doncd'après la remarque sur la page d'Euler et en considérant la fonction gamma comme un prolongement de la fonction factorielle sur R+.
Essayez n=3, on retrouve bien 4/3R3 !
De même, pour les surfaces, on peut considérer qu'en dimension n, le volume de la sphère de rayon R peut être donné en fonction de sa surface par :
ce qui donne :
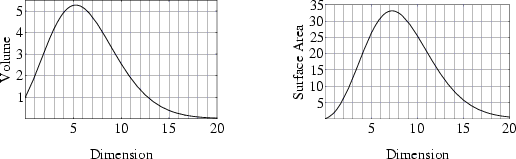
Ce qu'il y a d'amusant, c'est que ces formules valables pour tout n peuvent nous amener à la question : Le volume et la surface d'une sphère ont-elles un maximum pour une dimension donnée ?
La réponse semble oui dans la mesure où Vn et Sn tendent vers 0 si n tend vers l'infini (eh oui, la fonction gamma en n croit comme (n-1)! et donc beaucoup plus vite que la puissance du numérateur.
En dérivant les expressions de Vn et Sn par rapport à n, on trouve numériquement que le maximum pour la surface est en n=7,25695... et pour le volume en n=5,25695... !
Donc la sphère a un volume maximal en dimension 5 et une surface maximale en dimension 7 !
Voici d'ailleurs les graphiques du volume et de la surface en dimension n de ces "hypersphères", empruntés à la fabuleuse encyclopédie d'Eric Weisstein.
Si, si, c'est très sérieux...
Fagnano et les complexes
On peut s'amuser éternellement avec les nombres complexes... Il paraît qu'un certain Fagnano nous a gratifiés des deux formules suivantes :
Notons tout de même qu'en utilisant le DLpour z complexe avec la deuxième formule, on finit par retrouver :
ce qui n'est rien d'autre que la formule de Leibniz !
Pi et les espaces euclidiens
Lors de l'épreuve du Capes externe de mathématique en 1994, consacré à l'étude du rayon minimum des disques d'un plan affine euclidien contenant k points à coordonnées entières, les candidats devaient montrer le résultat suivant :
Soit D le disque de centre z0 et rayon r :
D(z0,r)={zC
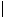
z-z0
r}
et rk=min{r>0,z0
C, card(Z[i]
D(z0,r))
k}
alors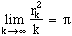
retour à la page d'accueil