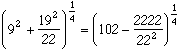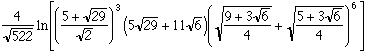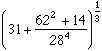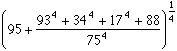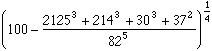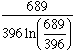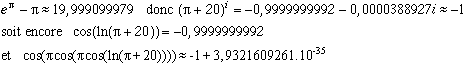Approximations et bizarreries sur Pi

Cette page est ainsi consacrée aux approximations rationnelles et irrationnelles qui se rapprochent le plus de Pi. Et il y en a de fameuses !
Sans oublier quelques curiosités approximatives concernant Pi.

En effet, depuis que l'on s'est rendu compte de l'existence d'une constante définissant le rapport du périmètre d'un cercle sur son diamètre, ce qui se situe à l'époque des Egyptiens et Babyloniens, les mathématiciens ont tenté de donner une valeur exacte de Pi, ou ont ensuite donné des approximations simples de Pi après le XVIIIe siècle.

Dans l'antiquité

Bien sûr, dans l'antiquité, ces mathématiciens ne savaient pas que Pi était irrationnel, ni même transcendant. Alors on tenait certaines valeurs estimées de Pi pour exactes !
Tout ce cheminement dans l'antiquité est relaté sur la page de l'ère géométrique, je rappelerai seulement ici les valeurs :
Donc, les Babyloniens avaient estimé :

ce qui est assez remarquable pour l'époque.
Le scribe Ahmès chez les Egyptiens avait obtenu :

=(16/9)²=3,16...

La Bible est resté célèbre pour son estimation hasardeuse de Pi : 3 !!

On se rappelle qu'Archimède avait encadré Pi, ce qui prouve qu'il avait conscience de ne pas être tombé sur la bonne valeur.

En Chine, Tsu Chung Chih devance les occidentaux et propose :

355/113 = 3,14159292...

Mais revenons en Occident. Tentant toujours d'obtenir une valeur exacte pour Pi, Nicolas de Cues propose :

Le plus fort reste sans aucun doute Edward Johnston Goodwin (1828-1902) qui déposa, en 1897 dans l'Indiana aux Etats-Unis, un projet de loi où diverses formules appliquées auraient conduit à assigner pour valeur à Pi : 4, puis 3.1604, puis 3.2 et enfin 3.232 !
Bien sûr, cet auteur ingénieux avait résolu la quadrature du cercle, la trisection de l'angle et la duplication du cube, démontrées insolubles quelques années auparavant, et avait accepté que ses découvertes soient utilisées gratuitement ! Même la prestigieuse revue American Mathematical Monthly, alors jeune, avait accepté deux de ses articles !
Heureusement, ce projet, qui faillit être adopté, fut repoussé finalement car on considérait alors que la loi ne devait pas décider de la vérité scientifique... encore heureux...

Après la renaissance

La démonstration de l'irrationnalité en 1761 puis de la transcendance en 1882 ont tout de même, à l'exception donc de ce farfelu de l'Indiana, miné les espoirs des amateurs et mathématiciens de proposer une valeur exacte pour Pi. A ce moment, les amusements vont commencer puisque l'on va rechercher des approximations rationnelles ou irrationnelles de Pi sous une forme simple. Et l'imagination et la patience des mathématiciens est fertile !
Jugez plutôt :

Quelques approximations :

Note : Jean-Christophe Benoist m'a fait remarquer avec pertinence que l'on classait souvent dans les livres (Delahaye, Warufsel...) les approximations de Pi en fonction du nombre de décimales exactes qu'elles donnaient. Avec ce principe, 3.14151 est mieux classé que 3.1416 alors que la seconde approximation est la meilleure. En outre, on ne peut pas départager deux approximations ayant le même nombre de décimales exactes !
Il m'a alors proposé de considérer le score -Log₁₀(|approximation-Pi|) comme critère de classement, ce qui a l'avantage de prendre en compte la réelle distance avec Pi ! J'ai donc inclus entre parenthèses quelques valeurs de ce score pour les plus petites approximations.

Formules	Valeur approchée	Décimales de Pi exactes
	3,1409	2 (3.21)
Approximation de Kochansky
	3,141533	4 (4.23)
Approximations de Ramanujan
=	3,14164	3 (4.32)
	3,14182	3 (3.63)
	3,141623	3 (4.51)
	3,14164	3 (4.32)
	3,14159265258	8 (8.99)
	3,14159265258	8 (8.99)
	3,14159265380	9
	3,14159265358979432	14
	3,14159265358979265	14
	3,14159265358979312	15
	3,1415926535897932384190	19
	3,141592653589793238462642088	23
	3,141592653589793238462643383279	30
Approximations de Castellanos (1988)
(2e3+e8)1/7	3,14171	3 (3.91)
	3,141529	4 (4.20)
	3,141575	4 (4.76)
	3,14159704	5 (5.36)
	3,141592452	6 (6.70)
	3,14159259259	6 (7.21)
	3,141592649	7 (8.41)
	3,141592654111	8 (9.28)
	3,14159265363	9
	3,14159265358817	11
	3,14159265359037	10
	3,141592653589780419	13
Approximations de Plouffe
437/23	3,1415398	4 (4.28)
	3,1415943	5 (5.77)
	3,14159267809	7 (7.61)
	3,14159259508	6 (7.23)
	3,14159265258	8 (8.99)
	3,14159265297	8
	3,141592653492	9
	3,1415926535949	10
	3,141592653586778	11
	3,1415926535912	10
	3,141592653589793238462649201	23
	3,1415926535897932384626433832797	30
Approximation de Stoschek
	3,141104	3 (3.31)
Et quelques autres
	3,141592920	6 (6.57)
=	3,1415333	4 (4.23)
103993/33102 (Euler)	3,14159265301	9

A noter que Ramanujan (1913) et Olds (1963) ont donné une justification géométrique de l'approximation 355/113. Gardner (1966) s'est occupé de celle de . Dixon (1991) s'est quant à lui intéressé à et =.

---

Curiosités

Toutes les formules précédentes sont en elles-même des bizarreries, puisqu'il suffit de retourner la formule pour qu'une expression incluant Pi donne presque un entier ou une fraction rationnelle ou irrationnelle.
L'exemple le plus fameux est celui des expressions de Roy Williams en avec n entier naturel :
Pour certaines valeurs de n (notamment parmi les nombres de Heegner 1,2,3,7,11,19,43,67 et 163), on trouve presque un entier :

n	Valeur de
25	6635623,999341134233266067
37	199148647,999978046551856766
43	884736743,999777466034906661
58	24591257751,999999822213241469
67	147197952743,999998662454224506
74	545518122089,999174985664301733
148	39660184000219160,000966674358575246
163	262537412640768743,999999999999250072
232	604729957825300084759,999992171526856431
268	21667237292024856735768,000292038842412959
522	14871070263238043663567627879007,999848772648279480
652	68925893036109279891085639286943768,000000000163738644
719	3842614373539548891490294377805829192,999987249566012187

En 1975, nous raconte le Fascinant Nombre Pi, Martin Gardner avait utilisé le cas n=163 pour faire un poisson d'avril en avançant que était un entier, ce qui, à l'époque, n'était pas facile à contredire ! En fait, ce cas particulier extraordinaire proviendrait du fait que le corps de nombres algébriques engendré par 163^1/2 possède une propriété de factorisation unique, les nombres de Heegner ayant des qualités arithmétiques particulières.

Précisons :
Ramanujan, (forcément !) avait remarqué que est un entier à 10^-12 près ce qui est vraiment étonnant. Son raisonnement par la théorie des fonctions modulaires ne fut percé que plusieurs dizaines d'années plus tard.

Il repose sur la même fonction j que celle présentée sur la page des Borwein, où l'on prend tout d'abord (t complexe). Cette fonction est modulaire, c'est à dire qu'elle est définie sur le demi-plan complexe supérieur, qu'elle admet une limite en , qu'elle est méromorphe et surtout invariante par la transformation (a, b, c, d entiers).

On définit maintenant une relation d'équivalence sur les formes quadratiques a.x²+b.xy+c.y² avec a, b, c dans Z et premiers entre eux (a>0 également).

Leur discriminant d=b²-4ac<0 est donné.

On définit la relation ~ par a.x²+b.xy+c.y² ~ a'.x²+b'.xy+c'.y² si on peut passer d'une forme à l'autre par la transformation :

Cette relation d'équivalence conserve le discriminant d. Le nombre de classes d'équivalences est noté h(d) et un célèbre théorème dû à Heegner (52), Baker et Stark (66) affirme que :

Ces entiers sont appelés nombres de Heegner.

En outre, Weber a montré que :

On obtient donc que .

D'autre part, en tant que fonction méromorphe, j admet un développement de Laurent en q qui donne :

Avec la valeur précédente , on obtient :

n entier, ce qui achève la démonstration.

L'approche algébrique montre que les entiers de Heegner sont très importants. Les corps quadratiques imaginaires engendrés comme possèdent des propriétés de factorisation fascinantes. Par exemple, son nombre de classe est 1 ce qui est équivalent au fait que la décomposition en facteurs premiers est unique dans ce corps.

Une autre curiosité est le nombre :



Moins de 1 millième d'erreur avec 20 pour un nombre aussi simple, voilà qui est étonnant, n'est-ce pas ?