Isaac Newton
(1642 - 1727)

(1) (2)


Une suite similaire :

(3)

Tranches de vie

Isaac Newton naquit le jour de Noël 1642. De famille humble, il se montra très inventif dès son enfance. Entrant à l'université de Cambridge en 1660, il rencontra un professeur et ami qui sera déterminant dans sa formation, Isaac Barrow.
Newton maîtrise rapidement les mathématiques de son époque. Mais la grande peste (1665-1666) l'oblige à retourner dans son village natal de Woolsthorpe, ce qui lui donne du temps pour ses recherches mathématiques et physiques.
Et quelles recherches ! Lois du mouvement des astres (attraction universelle), loi de l'optique sont brillament abordées et Newton découvre le calcul différentiel (rien que ça) grâce à sa méthode des fluxions (x+x^.o ou x+dx en notation moderne, enfin si l'on veut, puisqu'elle a été inventée par son grand rival Leibniz !)
Grand rival car celui-ci et Newton se querelleront violemment sur la paternité de l'invention de l'analyse différentielle jusqu'à la fin de leur vie. Les notations x^. ou x¨ de Newton ont tout de même perduré en physique...
La disparition de Newton le 20 mars 1727 provoque un deuil scientifique rarement égalé en Angleterre. Il est d'ailleurs inhumé à l'abbaye de Westminster.

Autour de

Ce qui nous intéresse ici, c'est bien sûr et ces deux formules découlant d'une analyse ingénieuse qui est en fait un cas particulier du DL d'arcsin :

Démonstration

Démontrons la première formule de façon "moderne" et rapide avant de laisser place à l'ingéniosité de la méthode originelle de Newton pour la seconde formule !

Si l'on pose y=Arcsin(x), c'est à dire x=sin(y) pour -1<x<1, on obtient facilement :
dx=cos(y)dy=(1-sin²(y))^1/2dy donc :

Par une récurrence que je qualifierai de "presque" immédiate, on transforme :

Comme c'est une série entière de rayon de convergence 1 (immédiat également par le critère de d'Alembert), on peut intégrer entre 0 et x sur un compact inclus dans ]-1,1[ et on obtient alors :

Et là, toutes les fantaisies sont permises !
On peut remplacer x par n'importe quoi, pourvu que -1<x<1...
Pour x=1/2, on a :
ce qui est bien la première formule !

Ou bien on peut choisir



Pour la deuxième formule, repassons dans le monde de la géométrie :
Newton a entrepris une démarche assez originale que nous retranscrivons ici :
Considérons le cercle de diamètre AB=1 et OC=1/4 (donc =/3) :
Newton cherche à calculer l'aire du domaine en gras ACD (Notée a(ACD), notation tout à fait personnelle)

1. D'une part, =/3 donc 6a(AOD)=R²=/4 car R=1/2
D'où a(AOD)=/24 or ,


2. D'autre part, Newton considère que a(ACD) est égale à l'aire balayée par le segment [MN] entre le point A et le segment [CD], ce qui se conçoit aisément !!
On a par pythagore AN²+NB²=AB² or AN²=AM²+MN² et NB²=MB²+MN²
d'où AM²+MN²+MB²+MN²=AB²
et l'on obtient alors 2MN²=AB²-AM²-MB²=1-x²-(1-x)²=2x(1-x)
On en conclut donc que :

Comme on s'en prend à une série entière, on a parfaitement le droit de l'intégrer terme à terme. On trouve alors :


Chouette, non ?

En prenant en compte l'équation du quart de cercle (1-x²)^1/2 pour x variant entre 0 et 1, on obtient de même :

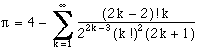
Essais

Ces suites ont une convergence quasi linéaire reconnaissable au premier coup d'oeil... Les essais ne sont donc a priori guère surprenants !

n=...	Suite 1	Suite 2	Suite 3
5	3,1415767 (4)	3,1415950 (5)	3,170 (1)
10	3,141592646 (7)	3,1415926541 (8)	3,15256 (1)
50	33 décimales justes	34 décimales justes	3,1426 (2)
100	63 décimales justes	65 décimales justes	3,141965 (3)

Les deux premières répondent bien aux attentes avec des convergences respectives d'environ 0,63n et 0,65n (les ajouts logarithmiques sont négligés !). Par contre, la suite 3 est très décevante. Tiens, voyons pourquoi...

L'équivalence de Stirling nous donne :




Ce qui confirme bien l'extrême lenteur de la suite 3 (convergence logarithmique) et la relative rapidité des suites 1 et 2 (convergence linéaire !). De plus, Log(4)=0,60... ce qui est également conforme aux observations !
Méfions-nous donc des séries en factorielles, certaines peuvent avoir une convergence logarithmique s'il n'y a plus de puissance au dénominateur dans l'équivalent du terme de la série... Heureusement, c'est assez rare...

A noter que le Delta2 d'Aitken est pratiquement inefficace sur ce genre de suites (on ne gagne qu'une décimale au maximum pour n100). Ca ne vaut pas le coup... Donc, pas de chapitre "Accélération de la convergence"!