Leonhard Euler
(1707 - 1783)

1) 1739

on pourra se référer à l'annexe : Nombres de Bernoulli. Pour plus d'infos sur les numérateurs et dénominateurs des nombres de Bernoulli, cf. A027641 et A027642 ou encore pour les Ber_2n A000367 et A002445.

2)


3) et 4) (1737)

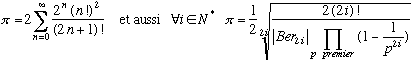
Tranches de vie

A l'image de sa production scientifique toute entière, Euler fut prolifique en ce qui concerne les formules sur .
Leonhard Euler est né à Bâle en 1707. Fils et petit fils de pasteur, Euler et sa famille sont pauvres. Son apprentissage ne comprend pas de mathématiques, ce qui le pousse à prendre des cours auprès d'un étudiant. A 13 ans, il commence des études de théologie et de philosophie dont il est diplômé à 16 ans. Son père le destine à devenir pasteur, il s'y prépare mais continue à étudier les mathématiques. Son talent est remarqué par Jean Bernoulli, un membre de la grande lignée de mathématiciens du même nom, et en 1727, il part à l'académie des Sciences de St-Pétersbourg. Le départ de Russie de Daniel Bernoulli lui permet de devenir professeur de mathématiques. Il rencontre alors la fille d'un artisan russe qui lui donne 13 enfants. Euler a une patience remarquable avec sa progéniture et est resté célèbre pour sa capacité à jouer tout en rédigeant un article. Il perd un oeil après une fièvre brutale.
Installé brièvement à la cour de Berlin sur l'invitation de Frédéric Le Grand, celui-ci préfère pourtant les esprits brillants comme Voltaire, et le traite de "Cyclope mathématique" (!). Revenu en Russie, il devient presque aveugle à partir de 1771... Il dicte néanmoins à son fils ses publications. Il meurt à St-Pétersbourg en 1783 en buvant du thé avec ses amis !

Autour de

Son oeuvre est immense... Ses travaux ont permis l'essor de l'analyse grâce aux équations différentielles et intégrales. Il aborda également la géométrie différentielle, la théorie des nombres et divers domaines de la physique. Ceux qui l'ont cotoyé le considéraient comme le plus grand mathématicien de tous les temps. Il faut dire qu 'il a publié près de 800 pages de texte scientifique par an soit au total 75 volumes de 600 pages chacun ! Infatigable, il a aussi imposé dans un souci de clarté de nombreuses notations comme e (pour la base des logarithmes néperiens), i pour les imaginaires et (surtout!) vulgarisé la notation (introduite en 1706 par W. Jones).
Sa rigueur est parfois contestable mais l'ingéniosité et la justesse des résultats sont remarquables. Un bon exemple en est la façon dont il a trouvé le résultat de la convergence de la somme des carrés des inverses et qui est relatée ci-dessous :

Démonstration

Pour les fondus d'analyse !!!
Par où commencer ? Bon, occupons-nous de l'égalité contenant les nombres de Bernoulli, la formule 1). Plusieurs démonstrations sont possibles, plus ou moins complexes... Celle présentée ci-dessous a le mérite d'être rapide (tout est relatif !) et repose sur la première définition des nombres de Bernoulli. Elle montre par ailleurs en complétant la démonstration suivante de la formule 2) l'équivalence des deux définitions des nombres de Bernoulli...
Puis juste après, la "démonstration" (hum!) originelle d'Euler pour la somme des inverses des carrés ! Si la rigueur n'est pas vraiment au rendez-vous, quelle imagination et quelle astuce !
Mais cela, c'est pour après la véritable preuve...

---

1) On ne pourra en effet jamais dire assez merci à Monsieur Fourier, sa théorie va nous être encore bien utile...

Considérant les polynomes de Bernoulli B_2n(t), prenons la fonction f_2n pour n entier, de période 1, et qui est égale à B_2n sur [0,1[. f_2n est évidemment C ¹ par morceaux car restriction de polynomes à un intervalle de R. Elle vérifie donc le théorème de Dirichlet pour les fonctions T-périodiques et on peut l'écrire sous forme d'une série de Fourier.

1.1 Premier petit résultat intermédiaire :

1.2 Calculons maintenant les coefficients de Fourier. Pour ne pas s'embêter inutilement, montrons tout d'abord par récurrence sur n que B_2n est paire par rapport à x=1/2...
B₀=1 par calcul immédiat donc pas de problèmes au rang 1...
Supposons pour un certain n entier que B_2n(x+1/2)=B_2n(1/2-x)
Soit g_2n+2(x)=B_2n+2(x+1/2)-B_2n+2(1/2-x). C'est un polynôme donc g_2n+2 est C² sur R.
d'après l'hypothèse de récurrence...
donc g'_2n+2 est constante... or, g'_2n+2(0)=(2n+2)B_2n+1(0)-(2n+2)B_2n+1(0)=0 donc g'_2n+2=0 donc g_2n+2 est constante or g_2n+2(0)=0 donc finalement, B_2n+2 est bien symétrique par rapport à x=1/2, c'est l'hypothèse au rang suivant donc la proposition est valable pour tout n entier et sur [0,1], f_2n est symétrique par rapport à x=1/2.
Donc on a le coefficient de Fourier associé b_k(f_2n)=
1.3 Calculons d'autre part pour n entier non nul
a_k(B_2n)=

= d'après 1.1 puis par récurrence descendante immédiate...
Jusque là, tout va bien ! Le reste n'est pas beaucoup plus compliqué... Il nous reste en effet à calculer a_k(B₂).

1.4 On pourra vérifier (puisqu'il y a unicité) que B₂=X²-X+1/6 est bien le polynôme de Bernoulli qui convient aux définitions. Par simple puis double intégration par partie, on a et . Et bien sûr, , donc, finalement,
a_k(B₂)= .
1.5 On a donc trouvé d'après 1.3 et 1.4

a_k(B_2n)=

1.6 Le développement de B_2n en série de Fourier nous donne alors pour t dans [0,1[ :
et donc en particulier pour t=0, on a :

où Ber_2n=B_2n(0)

et voilà !!!

Au vu de l'importance du résultat, cette démonstration est monstrueusement rapide par rapport à d'autres !!! Et en bidouillant un peu, on obtient également deux expressions bien utiles :

et

Plus généralement, on appelle sommes de Reynolds l'expression :

Donc, pour p=2n pair, on a la somme du dessus, et pour p impair, on a :


Ces nombres font intervenir les polynômes d'Euler dont je n'ai malheureusement pas trouvé la définition. Il suffit d'appliquer la méthode précédente aux polynômes d'Euler pour trouver le résultat.

Sinon, avec les premières valeurs des nombres de Bernoulli et la première formule, on obtient :
entre autres...

---

1) bis... Voilà donc la preuve originelle, d'Euler lui-même, de la somme des inverses des carrés... La convergence avait été démontrée par Jacques Bernoulli et Leibniz s'y était cassé les dents... voyons ce qu'Euler a fait. Il a trouvé la limite, mais les justifications sont un peu douteuses, vous verrez !

Se basant sur la théorie des équations algébriques, Euler savait que la somme des inverses des racines de a_nxⁿ+a_n-1x^n-1+...+a₁x+1=0 vaut -a₁. Considérant alors le développement de il sait grâce à la périodicité de sinus que le membre de droite s'annule pour x=²,4²,9²,16²...
Euler se dit alors que la propriété qui est vraie pour un polynôme fini doit l'être pour un polynôme infini et il en déduit soit . Très fort !

---

2) Bon, revenons à des choses un peu plus sérieuses (mathématiquement !)... La démonstration de la formule générale du 2) (abrégée, n'abusons pas du calcul, et de plus, je me sens un peu fatigué !) se trouve sur la page de Fourier. Une application z=1/2 donne :

.

Mais il y a plus fort ! Dans on développe en échangeant les sommes (z inférieur à 1 et absolue convergence des sommes)

En posant t=2iz et en calculant cotan au moyen de son expression en exponentielles complexes (cos/sin), on obtient

=

d'après la 2ème définition des nombres de Bernoulli. Ah ah !
Par identification des termes deux à deux (ce sont deux séries entières), on peut alors conclure

!!!

C'est effectivement le bon résultat montré en 1) et c'est aussi la méthode originelle qu'avait utilisé Euler. Voilà, 2 preuves pour le prix d'une ! Cela implique aussi l'équivalence des définitions des nombres de Bernoulli (ceux d'indice impair sont en effet nuls...)

---

3) Ouf, petite pause...

Bien, passons maintenant à la formule 3... Là encore, une astuce monstrueuse d'Euler intervient... Celui-ci utilise en effet un développement très inhabituel, mais ô combien efficace, d'arctan à savoir :

Arctan(t)=

pour t positif... Euler l'a utilisé avec une formule d'arctan =20Arctan(1/7)+8Arctan(3/79) pour calculer 20 décimales de Pi en une heure (essayez donc !). Il est vrai que si on pose t=1/7, =0,02 ! Pratique... Habile, Euler l'était certainement...
Voyons en effet sa démonstration :

3.1 Posons x=, t positif et x dans [0,1[.
On a t=. Posons maintenant y=Arctan(t)=Arctan

3.2 Essayons de simplifier l'écriture... Si z=Arctan, on obtient ce qui donne sin²z=x et donc

y=Arcsin.

Mais on n'y voit toujours pas très clair... Continuons donc...
3.3 On dérive cette expression par rapport à x et on obtient :

2y'(x-x²)+y(1-2x)=1

3.4 Cherchons y sous la forme y=. Inséré dans l'équation différentielle, nos yeux exorbités découvrent a₀+x(3a₁-2a₀)+=1+0.x+0.x²+... ce qui, par identification, nous donne a₀=1, 3a₁-2a₀=0 donc a₁=2/3, et (2n+1)a_n-2na_n-1=0 donc :

par récurrence immédiate sur n entier (calcul hyper classique !).
Réciproquement, on vérifie que y= convient comme solution de l'équation différentielle (à ne pas oublier, mais ne comptez pas sur moi pour le faire !).

3.5 Le reste est trivial commme disent certains... D'après la définition de y, on en conclut pour t réel positif :

Arctan(t)=

Mais que peut on faire de cela ? Plein de choses ! Tout d'abord appliquer la formule d'Euler décrite au début de cette section... Puis poser t=1 et obtenir la formule 3)... ou t=1/2, ou 1/4, ou utiliser les formules d'Arctan... tout est possible ! Comme d'habitude, plus t est petit, plus la convergence est rapide, car le terme en t dans la somme est de plus en plus petit...
Moi, j'aime bien t=, car on obtient avec Arctan(t)=/6 :

ce qui est très proche de la formule de Schroeppel-Gosper ! Chouette non ?

---

4) Bon, encore une démo... Au risque de paraître quelqu'un qui abrège de plus en plus au fil des démonstrations, je ne peux que donner les pistes de la démonstration de la formule 4)... D'après "Le fascinant nombre Pi" (voir Biblio) :
Soit a>1. Pour p nombre premier, p^a>1 donc par développement limité :

Si l'on écrit ces égalités pour tout nombre premier et que l'on fait leur produit, on obtient à gauche :

et à droite alors ? On obtient le produit des membres de droite, c'est à dire de sommes infinies. Si l'on élimine tous les produits infinis qui vont se former (des produits infinis de termes en 1/p^ka donnent 0 ne serait-ce que parce que 0<1/p^ka<1/2), il reste la somme de tous les termes de la forme , où p,q,r... sont des nombres premiers et k, i, j... des entiers... Cela ne vous rappelle rien ? Un certain théorème d'arithmétique qui dit que tout entier n est décomposable sous la forme p^kq ⁱr ^j... c'est à dire comme produit de nombres premiers chacun à une certaine puissance... Comme tous les nombres premiers et leurs puissances sont présents ici, on en déduit que cette somme infinie vaut :

Et pour a pair, on a alors d'après la formule 1) :

Ce qui est bien la formule 4), si l'on isole Pi !
Ces deux fabuleuses égalités trouvées par Euler seront réutilisées dans la page consacrée à Césaro. Une des conséquences importantes de ce résultat est que pour a=1, la somme des inverses diverge, donc le produit (membre de gauche) vaut l'infini, donc il existe une infinité de nombres premiers... Pas mal, non ? Voilà que Pi fait une entrée fracassante dans le monde de l'arithmétique !!!

Essais

Bon, avouons-le, toutes ces formules sont très belles mais ne sont pas vraiment faites pour le calcul des décimales... La forme des formules de type 1) promet une affligeante convergence logarithmique...

1)

n=10	3,0493 (0)
n=100	3,1320 (1)
n=1 000	3,1406 (2)
n=10 000	3,141497 (3)
n=1015	3,14159265358979228 (14)

une convergence d'environ 0.434*ln(n)-1, désespérant ...
A noter que j'ai trouvé sur Internet (mais je n'ai plus l'adresse) une suite accélérant un peu les calculs :

Mais la puissance dominante du bas étant 8, pas de miracles, cette suite converge moins vite que la suivante :

n=10	3,1415926535860 (11)
n=100	19 décimales justes
n=1 000	28 décimales justes
n=10 000	37 décimales justes
n=1010	92 décimales justes

Et une convergence d'environ 4ln(n)+0.5, si ça n'est pas malheureux !

2) Oublions la formule 2) du même genre que la 1) à un facteur et une translation près, ce qui ne change rien aux résultats...

3) La formule 3) s'avère un peu plus intéressante :

Je prends la version t= dans le développement d'arctan car, après tout, elle est plus rapide que la formule 3)...

n=5	3,14131 (3)
n=10	3,14159244 (6)
n=50	30 décimales justes
n=100	61 décimales justes

Ah, une convergence linéaire d'environ 3n / 5, déja plus accueillant...

Tiens, appliquons la formule de Machin avec le développement d'Arctan trouvé par Euler :

n=5	3,1415926500 (8)
n=10	15 décimales justes
n=50	74 décimales justes

Une convergence linéaire de 3n/2, ce n'est pas mal du tout !
Et enfin, appliquons la formule d'arctan trouvée par Euler pour calculer les décimales de Pi :
=20Arctan(1/7)+8Arctan(3/79)

n=5	10 décimales justes
n=12	21 décimales justes
n=50	88 décimales justes

7n/4 de convergence et l'on remarquera qu'Euler a dû calculer 12 itérations pour obtenir les 20 décimales de Pi... En 1 heure, cela paraît incroyable ! Tentez donc à la main.

4) Pour finir, la formule 4 n'a aucune vocation calculatoire et sa forme laisse augurer d'une convergence logarithmique, alors...

Accélération de la convergence

Tout petit paragraphe, car franchement, rien n'est terrible, même avec le Delta2 d'Aitken... Mais à convergence lente, présence du Delta2 qui décidément, sauve certaines suites d'un bide lamentable...
Pour :

n=1000	3,14111 (3)
n=10000	3,141544 (4)
n=100000	3,1415921717 (6)

environ log(n), pas si mal, mais tout de même...

Et pour la formule d'arctan avec t= :

n=10	3,1415926520 (8)
n=50	34 décimales justes

Une convergence linéaire d'environ 7n/10. Mieux, mais pas de quoi déplacer les montagnes...