retour au grenier

Triangle des c(n,k)

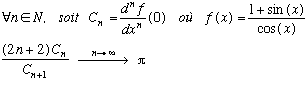
Références de l'Encyclopédie des Suites Entières : A008280 - A008281 - A008282

Autour de

La formule ci-dessus est l'expression analytique de la définition des c(n,k).
(dans ce cas, on a k=n)

Mais en 1966, Entringer fut le premier à construire le tableau ci-dessous qui résulte de la répartition des permutations up-down suivant les valeurs de leur premier terme.
Pour ce faire, formons le triangle des entiers c(n,k), (0kn) dans lequel chacun des entiers c(n,k) ( à ne pas confondre avec les combinaisons) est la somme des k derniers termes de la ligne n-1 :

c(n,k)	k=0	1	2	3	4	5	6	7	8
n=0	1
1	0	1
2	0	1	1
3	0	1	2	2
4	0	2	4	5	5
5	0	5	10	14	16	16
6	0	16	32	46	56	61	61
7	0	61	122	178	224	256	272	272
8	0	272	544	800	1024	1202	1324	1385	1385

Les nombres c_n semblent être connus depuis Euler et admettent comme définition celle du haut de la page.
En 1879, Désiré André leur a trouvé la propriété d'être également le nombre de permutations up-down des entiers de 1 à n (cela signifie que les n-1 différences successives de deux termes consécutifs de la permutation sont alternativement positive, négative positive, etc...). On appelle aussi cela dans notre bonne vieille langue de Molière les "alternantes" ou "alternances d'André" ce qui est bien mérité ! (merci pour cette précision de Serge Bouc)
Par exemple, c₄=5 et l'on a en effet 5 permutations up-down de {1,2,3,4} :
1 3 2 41 4 2 32 3 1 42 4 1 33 4 1 2

Pour 1 3 2 4, on a bien 3-1=2, 2-3=-1, 4-2=2

Notons ensuite c_n=c(n,n). on a alors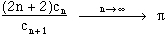

Principe de la démo

En fait, on peut montrer que la série entière de terme général admet /2 pour rayon de convergence, (ce qui semble logique si l'on considère la validité du développement de Taylor de la fonction f définie comme en haut).
Donc, le rapport des coefficients devant zⁿ tend alors forcément vers /2 d'après le résultat de d'Alembert.

Essais

La fraction donne une valeur approchée de Pi par défaut si n est pair et par excès sinon :

n=0	1	2	3	4	5	6	7	8	9	10
2	4	3	3,2	3,125	3,147	3,1397	3,1422	3,14138	3,1416	3,141569

On dirait une convergence logarithmique, mais je n'en ai pas la preuve...