Lord William Brounker
(1620 - 1684)

Formule importante

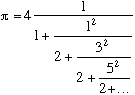
autres fractions continues...

Référence de l'Encyclopédie des suites entières : A001203

Tranches de vie

De formation linguistique et philosophique (doctorat en 1647 à Oxford) et fondateur avec Wallis de la Royal Society, William Brounker se passionne néanmoins pour les mathématiques. Sur la demande de son ami Wallis, il entreprend des recherches sur et les fractions continues, ce qui lui permet de proposer le développement de /4 sous cette forme d'après la formule de Wallis.

Autour de

Il existe de nombreuses autres fractions continues faisant intervenir . Malheureusement, leur convergence n'est pas très rapide, elles sont inutilisables en pratique, mais proposent une autre façon de représenter les nombres que les décimales classiques. D'après certains, Ramanujan avait peut-être le don de penser les nombres en terme de fractions continues, ce qui expliquerait en partie ses étonnants résultats...

Démonstration

Un peu de théorie sur les fractions continues qui ont totalement disparu de l'enseignement ! La fraction réduite d 'une fraction continue généralisée s'écrit : .
On peut calculer les réduites P_n et Q_n par les formules de récurrence :
P_n+1=b_n+1P_n+a_n+1P_n-1 et Q_n+1=b_n+1 Q_n+a_n+1 Q_n-1 (notées (1) et (2)).
On a dans notre cas a₀=0, a₁=1, a_n=(2n-3)² pour n>1, b₀=1, b_n=1 pour n>1.
Une autre formule très utile est P_nQ_n-Q_nP_n-1=(-1)ⁿa₁.a₂.....a_n (3)
et enfin, la fraction converge ou non en même temps que la série
a₀+ (4) et a même limite en cas de convergence.
Bon, passons à la pratique et appliquons ces formules à la fraction de Lord Brounker... Montrons par récurrence, (c'est le plus pénible !) que la proposition A_n : Q_nQ_n-1= (H1) et =(2n-1) (H2) est vraie pour tout n>2.
Pas de problèmes pour n=2 puisque et Q₂ Q₁=3.
Après, c'est un peu plus lourd... Supposons le résultat pour un certain n>2.
On a d'après (2) Q_n+1Q_n=2Q_n²+(2n-1)²Q_n-1=2Q_nQ_n-1+(2n-1)²=(2+(2n+1)²)=(2n+1)(2n-1) d'après (H2)
= et c'est bien (H1) au rang suivant que l'on notera d'ailleurs (H3).
D'autre part, d'après (H1), (H2), et (H3)
donc finalement, =(2n+1) ce qui est bien (H2) au rang suivant. Le théorème de récurrence nous permet de conclure à la validité de A_n pour n>2.
Et avec (4) et la convergence de la série d'après Leibniz, on conclut que est bien la valeur de la fraction continue proposée par Lord Brounker...

Essais

Malheureusement, si la formule est belle, le fait que la fraction réduite converge comme la série de Leibniz implique des résultats éxécrables... (n'ayons pas peur des mots...). Les résultats étant les mêmes, se reporter à Leibniz pour le détail des essais...

Autres fractions continues (toutes aussi belles !!)