Gottfried Wilhelm Leibniz
(1646 - 1716)

(tout simplement !)

et une série dérivée :

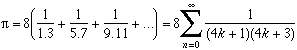
Tranches de vie

Leibniz est né à Leipzig en 1646. Mathématicien et philosophe allemand, toute son oeuvre est cependant écrite en français ou latin. Fils de professeur de philosophie, sa formation n'est que très peu mathématique, mais il se découvre une passion pour elle grâce à Huygens avec qui il se lie d'amitié.... (merci Huygens !)
Leibniz s'intéresse surtout aux séries numériques - Ah ! voilà qui est intéressant - et affirme sa paternité du calcul différentiel, ce qui lui vaudra une violente querelle avec Newton et assombrira la fin de sa vie.
On ne le sait pas toujours, mais ce bon vieux Leibniz est un grand inventeur de notations. On lui doit les signes (intégrale), = , dx , . pour la multiplication et : pour la division.
Mais Leibniz, malgré son génie, n'avait pas une idée très précise des nombres complexes par exemple et écrivait des lignes entières d'égalités sans grand sens comme :

avec laquelle il étonna Huygens...
Ses conceptions philosophiques influençaient grandement sa vision mathématique... Il considérait ainsi ces fameux nombres complexes comme amphibie à mi-chemin entre existence et non-existence !
Ignoré à sa mort par les communautés scientifiques allemandes et anglaises, notre célèbre centenaire Fontenelle fit néanmoins son éloge à Paris... Il l'avait bien mérité !

Autour de

Alors là, il y a un peu d'abus de ma part, car Leibniz n'est pas vraiment le découvreur de cette formule. James Grégory (1638-1675) avait en effet calculé le développement en série entière :

arctan(x)=

pour x entre -1 et 1. Il serait étonnant que Grégory n'ait pas vu le cas particulier x=1 qui donne la formule :

Mais comme nous allons le voir, sa convergence est plus qu'exécrable et Grégory a dû se rendre compte du peu d'intérêt qu'offre la formule en pratique... Mais avouez qu'elle est très belle et d'une simplicité remarquable ! Donc rendons à Grégory ce qui lui appartient, même si la première publication de cette formule est seulement explicitée dans l'oeuvre de Leibniz...
D'autre part, cette formule de Leibniz/Grégory réserve quelques surprises, découvertes très récemment par Roy North... Allez donc voir la section essais !

Démonstration

Que dire de la démonstration tant elle paraît un peu évidente...
On se rappellera que arctan : R->]-/2,/2[ est définie comme la fonction réciproque de la bijection tan : ]-/2,/2[->R.
Or, on a tan'(x)=1+tan²(x) (en passant par les cos et sin) et donc d'après la formule de la dérivée d'une fonction réciproque .
Or on connaît la série entière définie sur ]-1,1[. On sait que l'on peut l'intégrer terme à terme sur cet intervalle d'après les propriétés des séries entières. Après avoir remarqué que le résultat obtenu converge en 1 et -1 ce qui assure la convergence uniforme de la série sur [-1,1] vers arctan, on fait x=1 et le tour est joué... On peut également utiliser x=1/3^1/2, ce qui est plus intéressant :

Essais

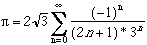
Attention, grand moment !
Pour la formule de Leibniz/Grégory :

n=10	3,2323 (0)
n=100	3,151493401 (1)
n=1 000	3,14259165 (2)
n=10 000	3,1416926435905432 (3)
n=100 000	3,14160265348979398846014336 (3)
n=500 000	3,141590653589793240462643383269502884197 (5)
n=1 000 000	3,14159365358879323921264313 (5)

Si il y a quelques décimales en marron, c'est parce qu'elles sont fausses! Mais alors, pourquoi les suivantes sont-elles justes? Car enfin la convergence est bien logarithmique d'après la forme (environ log(n)) ! C'est le problème que Roy North a posé aux frères Borwein il y a quelques années... Je n'ai plus la solution, mais elle fait intervenir les nombres d'Euler et deux formules de sommation. En attendant des recherches ultérieures...

Pour la seconde formule (juste au dessus de la section Essais) on a une intéressante convergence linéaire d'environ n/2 :

n=10	3,1415933045
n=100	49 décimales justes

Accélération de la convergence :

Si il y a bien une suite pour laquelle le Delta2 d'Aitken est vraiment, mais alors vraiment utile, c'est bien celle de Leibniz... Et d'autres formes d'accélération marchent aussi ! Car, une convergence logarithmique, ça n'est guère convaincant...

1) Avec le Delta2 : accélération classique et de plus en plus rapide normalement... requiert un calcul avec beaucoup de décimales à cause de l'instabilité numérique du procédé.

2) Avec une moyenne :
Puisque c'est une suite alternée, j'ai eu l'idée d'appliquer une moyenne à la suite de Leibniz. Ce qui n'aurait dû en théorie qu'apporter au mieux 1 décimale de plus se révèle accélérer la convergence de la suite de façon surprenante ! :
on note la moyenne pondérée associée.

Les résultats apparaissent dans le tableau ci-dessous pour les 2 types d'accélération :

	Leibniz	Delta2	Moyenne
n=3	2,8952 (0)	3,13333 (1)	3,161904 (1)
n=5	2,976 (0)	3,13968 (1)	3,143434 (2)
n=10	3,2323 (0)	3,141839 (3)	3,14150053 (4)
n=100	3,15149 (1)	3,141592905 (6)	3,14159264593 (7)
n=1000	3,142591 (2)	3,141592653839792 (9)	3,141592653589041 (12)
n=10000	3,14169264 (3)	3,1415926535900 ? (10)	3,1415926535897931634 (15)

Le dernier résultat pour le Delta2 me paraît douteux, surtout au vu du résultat de la moyenne, je l'ai calculé avec 100 décimales pourtant...

Ce qu'il y a de bien avec les suites construites à partir d'autres, c'est que l'on peut réitérer le procédé.
Application tout de suite !

	Delta2 itéré 2 fois	Moyenne itérée 2 fois
n=3	3,13888 (1)	n'existe pas...
n=5	3,141450 (2)	3,1215 (1)
n=10	3,141595655 (5)	3,141598653 (5)
n=100	3,1415926536094 (9)	3,141592653589922 (12)
n=1000	3,1415926535897934269 (15)	3,14159265358979323847405 (19)
n=10000	trop douteux !!	3,14159265358979323846264338440 (26)

A noter que les combinaisons entre Delta2 et moyenne sont moins efficaces...

3) on peut aussi réordonner les termes comme l'avait fait Leibniz, mais ce n'est guère plus efficace.

Bon, cette fois-ci, je crois que c'est tout concernant cette suite finalement très riche !!