blason de l'Ecole Polytechnique

Fabrice Bellard
(1973)

avec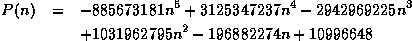

Tranches de vie

Fabrice Bellard est un garçon assez exceptionnel. Peut-être un des plus doués de notre génération. Après des études brillantes au lycée et en prépa à Joffre (Montpellier) où déja, il conçoit un logiciel de compression des données sans perte (le fameux LZEXE), il entre en 1993 à l'école Polytechnique (76e au concours sur 6000 candidats). Il choisit ensuite Télécom Paris comme école de spécialisation en 1996.
Concepteur de nombreux logiciels dans des domaines aussi variés que la compression, la 3D, la musique, c'est assurément un informaticien de tout premier plan !
A seulement 25 ans, son expérience professionnelle et ses réalisations sont déja impressionnantes comme on peut le voir sur son site.

Autour de

Après quelques calculs en 1995, Fabrice Bellard s'est intéressé de plus en plus à Pi et a notamment découvert les deux formules du haut au moyen de l'algorithme PSLQ, qui permet de tester certaines relations numériques. Notons néanmoins que la seconde n'est pas démontrée...
De plus, Simon Plouffe a élaboré en 1996 un algorithme pour calculer en système décimal (et non plus en hexadécimal comme la formule BBP) le n-ième digit de Pi. Malheureusement, sa complexité en O(n³log(n)) le rendait inutilisable en pratique. Eh bien, Bellard s'y est tout simplement plongé et a amélioré l'algorithme en O(n²) ! Rien que cela !
Mais son grand coup d'éclat reste le calcul en binaire du 1000 milliardième digit de Pi (qui est un 1 en passant) utilisant plusieurs stations dont des Ultrasparcs...
Le record actuel est le 40 000 milliardième digit en binaire de Pi (0) par Colin Percival. (Jusqu'où irez-vous ? comme diraient certaines personnes désagréables avec le monde Apple... blague publicitaire française...)

Démo

Eh bien voici le résumé de la démonstration telle que Fabrice Bellard la donne, pour la première formule. Pour la seconde, j'ai trouvé une démonstration, voir la page Hypergéométrique.
On considère avec z<1
donc en particulier :
(1)
(2)
Si l'on fait a=2 dans (1), on obtient :

Il suffit ensuite de considérer les relations en arctan :

Et avec la relation (3) et (1), on obtient :


ce qui, en réordonnant les termes, permet d'obtenir la formule finale du haut de la page...

Essais

Allons y ! Cette formule améliore en théorie de 43% le calcul avec la formule BBP. La forme nous indique que la convergence est en 10.n.log(2)=3n environ ce qui est bien !

n=0	3,1417
n=2	9 décimales justes
n=5	19 décimales
n=10	34 décimales
n=20	64 décimales

Et pour la deuxième formule :

n=1	0,02452 !
n=5	3,1416
n=10	12 décimales
n=20	32 décimales
n=50	94 décimales

Eh bien voilà une convergence qui s'accélère ! Du moins au début car passé les premières valeurs de n, cela va se stabiliser. En appliquant l'équivalence de Moivre/Stirling au terme de la série, on trouve d'ailleurs que la rapidité de convergence est en 2.12*n-5*log(n) environ, ce qui est tout de même assez correct.