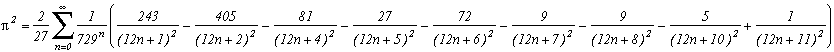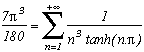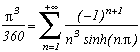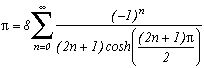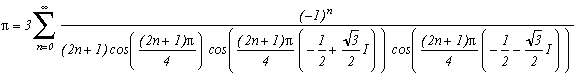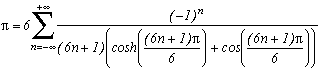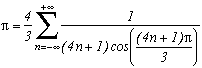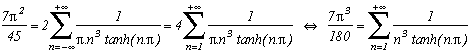Simon Plouffe / David Bailey
(pour voir d'autres photos, cliquez sur celles ci-dessus)

Formules dérivées

Formule d'Adamchik-Wagon

Autres formules :

Identités de Plouffe/Ramanujan/Borwein sur les (2n+1) (voir page perso de Plouffe)

Formule originale :



ce qui donne par exemple :






Autres formules du même type auxquelles on peut aboutir :

Tranche de Vie

Le mieux pour David Bailey, c'est d'aller voir sa page personnelle.
En résumé, il a passé sa thèse en mathématiques à l'université de Stanford en 1976. Il a tout d'abord travaillé au département de la défense, puis à la Nasa, et travaille maintenant dans le laboratoire Lawrence de Berkeley depuis 1998. C'est un spécialiste des détections de relations entières entre nombres et de processus de calcul rapides. (Et lorsque je dis spécialiste, c'est vraiment une bête comme on dirait chez nous !)
Concernant Simon Plouffe, son site est de même assez instructif. C'est une personne vraiment gentille et disponible, je vous assure que c'est toujours pour moi une fascination de pouvoir parfois discuter avec de telles personnalités du monde mathématique sans être pris de haut. Il a sinon passé son DEA (maitrise au Canada) de maths sous la direction de François Bergeron, qui est maintenant professeur à l'uqam. Il a ensuite passé quelques années à l'université de Bordeaux en tant qu'assistant de recherches dans les années 80, puis a rejoint l'uqam, plus présicément le laboratoire de combinatoire et d'informatique, la LACIM.

Autour de

Vous avez d'ailleurs peut-être déja lu le nom de Simon Plouffe sans vous en rendre compte... Il figurait en effet dans le Guinness des Records en 1975 pour avoir réussi à mémoriser 4096 décimales de... Pi (tiens, comme c'est étonnant !). Après avoir atteint 4400 et s'être arrêté, il a continué ses recherches sur Pi jusqu'à ce 19/09/95, 0h29 où cette célèbre et fameuse formule BBP (Bailey-Borwein-Plouffe) lui est apparue sur son ordinateur...
Le fascinant nombre Pi de J.P. Delahaye explique bien mieux que je ne pourrais le faire ici les procédés assez simples où interviennent les congruences, les divisions euclidiennes et transformées de Fourier rapides qui permettent d'atteindre en base 16 ou, plus généralement en base 2ⁿ, n'importe quel "décimale" de Pi. (Ce ne sont alors plus des décimales, mais des digits...) En fait, si on imagine vouloir obtenir le milliardième digit en base 16, il suffit de savoir calculer le milliardième digit de 1/(16ⁱ), ce qui est simple avec les congruences, et de gérer habilement les retenues qui peuvent apparaître dans les termes en a/(b+c*i) en calculant quelques termes avant et après. Je préciserai un peu plus prochainement, c'est promis...
Malheureusement, une série permettant le calcul du n-ième chiffre en base 10 et rapidement est toujours introuvable... Avis aux amateurs !
Plouffe a développé avec son astuce habituelle une méthode partant d'une série semblant anodine, mais dont sa complexité en O(n³log(n)) le rendait inutilisable en pratique. Fabrice Bellard s'y est tout simplement plongé et a amélioré l'algorithme en O(n²) mais malgré cela, on est encore assez loin de ce côté là d'une formule vraiment utilisable.

Démonstration

* Formule BBP

Par contre, je ne passerai pas outre la démonstration de cette merveille de formule BBP. Elle est d'ailleurs étonnamment simple mais l'imaginer fut certainement le plus difficile... :
Calculons tout d'abord un petit résultat général :

(l'inversion somme-intégrale est parfaitement justifiée puisqu'il y a convergence uniforme de la série sur [0,2^-1/2] )
Donc, si l'on applique ce résultat à la suite BBP, on a :

on fait un petit changement de variables y=2^1/2x pour y voir plus clair...
= par décomposition en éléments simples...
= en bidouillant un peu...
==


* Pour les identités de Plouffe

Montrons la première identité, les autres sont vraiment du même genre :
Considérons la fonction de la variable complexe . D'après l'étude sur la page Estenave/Frétigny, son intégrale sur un contour carré infini est nulle, donc la somme des résidus de cette fonction est nulle. Voici le tableau des pôles / résidus :

Pôles	Résidus
0
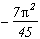
n
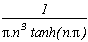
i.n
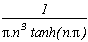
somme des résidus des racines	0

finalement on a donc :


pour obtenir l'identité avec (3), on coupe la somme :

et voilà !
Tout l'intérêt de ce résultat, outre l'esthétique, provient du fait que l'on peut ainsi accélérer le calcul des décimales de (3). On connaît en effet plus de 200 milliards de décimales de et il suffit de ne calculer que la valeur précise de exp() dans la somme de droite pour pouvoir calculer le reste de la somme facilement. On obtient une convergence linéaire d'environ 2.72n bien sympathique. Simon Plouffe nous assure qu'il a calculé de cette manière 30 000 et 50 000 décimales de (5) et (7) respectivement. Et plusieurs millions sont possibles. une bien belle astuce en somme !

Les autres formules du même type en cos et cosh proviennent de la page de Estenave/Frétigny. Elles ont été obtenues également pas le théorème des résidus mais d'une autre manière, un peu moins propre...

Essais

La formule BBP n'a pas été créée pour calculer les décimales de Pi en partant des premières, mais procédons à quelques essais néanmoins... La forme elle-même donne directement les performances en vertu de la petite inégalité écrite dans la rubrique précision de la page consacrée à Machin.
A savoir donc, une précision de 2+log(8n)+n*log(16), ce qui est honorable mais pas exceptionnel :

n=1	3,14142 (3)
n=5	3,141592653228 (9)
n=10	15 décimales justes
n=50	64 décimales justes

Accélération de la convergence

Comme il fallait s'en douter après ses médiocres performances auprès de la suite de Machin, le Delta2 d'Aitken n'est pas vraiment efficace ici...

n=5	3,1415926535630
n=10	17 décimales justes

Le nombre de décimales avec lequel on calcule la suite d'Aitken est très élevé à cause de la sensibilité du Delta2, donc il vaut mieux ici pousser la série BBP quelques termes plus loin...