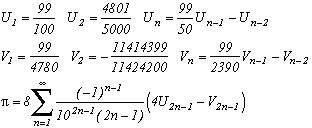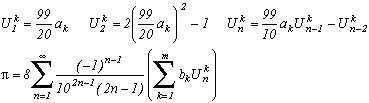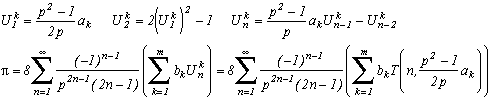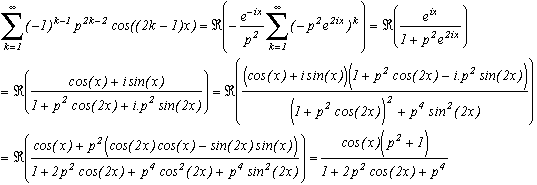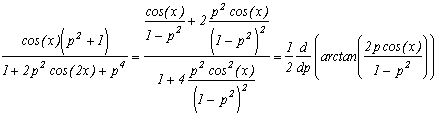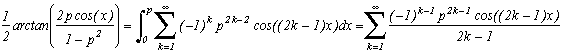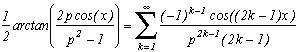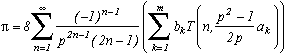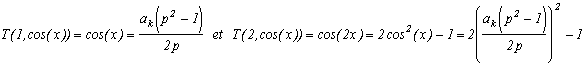Polynômes de Chebyshev, Pi, et le "look BBP"

Un premier exemple :

Notez que c'est une série de termes rationnels ! Les suites U_n et V_n ne sont rien d'autre que des valeurs des polynômes de Chebyshev, respectivement T(n,99/100) pour U_n et T(n,99/4780) pour V_n.
Et pour les petits malins qui auraient déjà remarqué une certaine ressemblance des coefficients de récursivité de U_n et V_n avec les formules d'Arctan (pensez à Machin !), bien joué, voici une formule plus générale où l'on utilise ces fameuses formules :
Si l'on connaît une relation du type : alors on peut construire les suites U_n^k et la série suivante :
Vous voulez autre chose que le 10 au dénominateur ? Soit, voici une formule encore plus générale pour p²>1, toujours en partant de la relation avec les Arctan :

avec T(n,x) le polynôme de Chebyshev.

Mais d'où ça vient ?

Cet algorithme est un peu du même style que les séries type Machin, mais ici on se permet d'avoir un dénominateur commun aux puissances (10 dans notre premier exemple). Ces formules n'ont malheureusement de la série BBP que l'apparence. Car si on a enfin obtenu un 10 au dénominateur au lieu du 16 de la formule BBP, et que le reste de la somme est rationnel, celui-ci est une fonction de puissances. En effet, les suites U_n et V_n sont récurrentes, on peut donc en trouver un terme général sous la forme U_n=a.r₁ⁿ+b.r₂ⁿ où r₁ et r₂ sont les racines de x²-c.x-d=0 tel que U_n=c.U_n-1+d.U_n-2. Pour Delta non nul bien sûr, mais allez me chercher une racine double ! Et même dans ce cas, on écrit U_n=(a+b.n)rⁿ où r est la racine double. a et b se déterminent ensuite grâce à U₁ et U₂, mais les expressions sont tellement horribles que je préfère ne pas perdre de temps à les écrire ici. De toutes les façons, comme d'habitude, il y a des racines dans l'affaire et l'on ne comprend même pas comment l'expression peut être rationnelle au final.
Là encore, je n'ai pas trouvé ce genre d'expression sur le net, et même le Gradshteyn ne la mentionne pas. Pourtant, c'est bien de ce livre que m'est venue l'idée et l'on va enfin voir dans la démonstration pourquoi j'ai appelé cette page Polynômes de Chebyshev et Pi.

Définition préliminaire des polynômes de Chebyshev

Un petit mot de Chebyshev (ou Tchebychev francisé) :
Né en 1821 à Okatovo dans une famille noble et cultivée, il fait ses études à l'université de Moscou. Sa famille ruinée, il refuse les postes d'enseignants qu'on lui propose et vit misérablement jusqu'en 1847 où il devient enseignant à Saint-Petersbourg. Il se met alors à voyager et à profiter de ses talents d'ingénieur, il est en effet très habile.
Par contre, il était infect avec ses élèves, n'aimant pas perdre son temps, et avait l'habitude d'arrêter ses cours à la seconde près au milieu d'une phrase, nous raconte "Des mathématiciens de A à Z".
Pendant sa carrière, il s'intéressa surtout à la théorie des nombres et fit grandement progresser les pistes de démonstration du théorème des nombres premiers.

On peut définir ses fameux polynômes au rang n par la relation suivante :
T(n,cos(x))=cos(n.x), T(0,y)=1
En d'autres termes, c'est le polynôme qui permet d'exprimer les cos(n.x) en fonction de cos^k(x), kn. Il est unique si l'on choisit de le rendre égal à 1 au rang 0 : T(0,y)=1.
En effet, il vérifie la relation de récurrence (géniale) suivante :

T(n,x)=2x.T(n-1,x)-T(n-2,x)

C'est elle qui va nous servir à construire les suites U_n^k.

Démonstration

Tout d'abord, nous avons besoin d'un petit calcul préliminaire :



A quoi cela va-t-il bien pouvoir servir ? Eh bien en remarquant que

on obtient

(la convergence de la série était uniforme sur tout compact inclus dans [0,1[ et p<1, ce qui justifie l'inversion de la somme et de l'intégrale)
C'est cette formule qui est relatée dans le Gradshteyn/Ryzhik (5e ed. 1.448.6). Retrouver la démonstration n'était pas bien difficile, du reste, vous aurez sans doute remarqué que j'avais honteusement fait les calculs à l'envers en premier lieu, car le "en remarquant que" plus haut n'est pas facile à voir directement !
Il suffit ensuite de remplacer p par 1/p<1 pour retrouver la formule que l'on utilisera par la suite :

Et arrivé là, je me suis dit : "Mais les cos(n.x), on les connait en fonction des puissances cosⁿ(x) grâce aux polynômes de Chebyshev, qui rappelons le, vérifient T(n,cos(x))=cos(n.x).
On considère alors la relation . On choisit alors x=x_k tel que . (oui, bon, il faut que le terme à l'intérieur de l'arccos soit inférieur à 1, mais même si cela n'est pas le cas, on obtient un x complexe et ça marche aussi finalement avec a_k=1...). Remarquons que si la relation sur les arctan est agréable, les a_k sont rationnels et grâce aux polynômes de Chebyshev, cos((2k-1)x)=T(2k-1,x) l'est aussi.
Avec cette expression, il vient :

Maintenant, c'est presque gagné, on utilise la relation de récurrence des polynômes de Chebyshev pour calculer les T(n,x).
Comme
et T(n,x)=2x.T(n-1,x)-T(n-2,x) on construit l'algorithme final :



Amusant, n'est-ce-pas ?

Essais

Dans le cas de la première suite, j'avais choisi p=10 et utilisé la formule de Machin. Voici les valeurs numériques :

n=2	3,141545
n=5	3,1415926535919
n=10	20 décimales
n=20	41 décimales

On remarque que la partie des polynômes de Chebyshev décroit très lentement puisque la convergence est quasiment de 2n, ce qui est dû au facteur 1/10² au dénominateur. A mon avis, c'est une solution alternative intéressante aux séries de type Machin...