université de Cambridge

S.C. Woon

Tranches de vie

S. C. Woon est étudiant chercheur dans le département de maths appliquées de l'université de Cambridge. Et... c'est tout ce que je sais de lui ! Il n'a en effet pas de page personnelle et ses publications sont encore rares. La formule qui nous intéresse est parue dans la prestigieuse revue American Mathematical Monthly en 1995 sous le nom très explicite de Problem 1441 !

Démonstration

Eh bien vous voulez une preuve ? La voici...
Montrons ainsi par récurrence que :

Pour n=0, pas de problèmes...
Supposons maintenant le résultat pour un certain n entier naturel non nul.
On a par hypothèse de récurrence.

Or,

donc en sommant, les terme de cotangente s'annulent deux à deux, cotan(/2)=0 et il reste

Mais on a aussi donc on obtient finalement

et c'est bien l'hypothèse de récurrence au rang suivant...

On conclut alors par le théorème de récurrence qui nous indique que le résultat est valable pour tout n entier naturel.
Ensuite, il est évident par équivalent de sin(x) et x en 0 que :

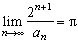
Essais

Cette drôle de formule est-elle efficace au fait ?
Eh bien ce n'est pas mal du tout :

n=	an
5	3,14033 (2)
10	3,1415914215 (5)
20	11 décimales exactes
50	29 décimales exactes
100	59 décimales exactes

Un tout petit peu moins de 0,6n mais une convergence linéaire tout de même, c'est intéressant !
La justification de la convergence linéaire peut être reprise de la démonstration sur la page de Cues où la suite b_n correspondait pratiquement à celle de cette page.

Accélération de la convergence

Comme toute bonne suite à convergence linéaire, le Delta2 d'Aitken accélère efficacement notre suite. Bien que ce soit les mêmes résultats que sur la page de Cues, je les remets pour vous éviter un chargement supplémentaire !

n=	an	Delta2(an)
5	3,14033 (2)	3,141595089 (5)
10	3,1415914215 (5)	3,1415926535921 (10)
20	11 décimales justes	23 décimales exactes
50	29 décimales exactes	59 décimales justes
100	59 décimales justes	...

Je ne peux toujours pas dépasser 100 décimales, en attendant que je me penche un peu sur Mathematica au lieu de Maple Etudiant que j'utilise habituellement...
Toujours est-il que la rapidité de convergence est doublée (presque 1,2n), ce qui est réellement impressionnant !