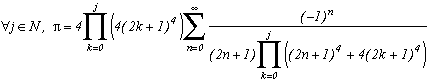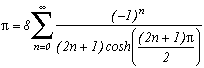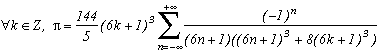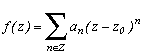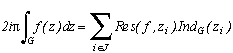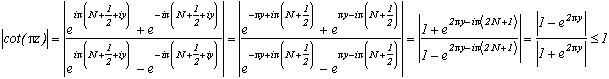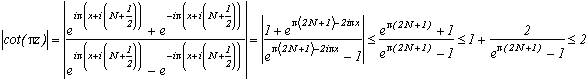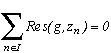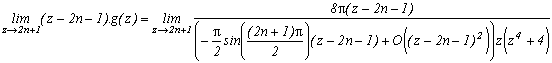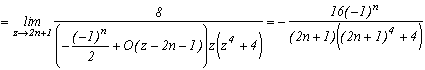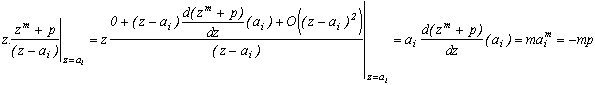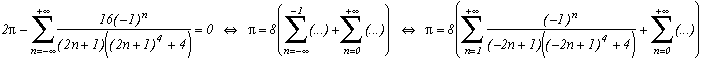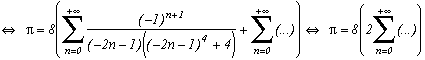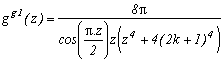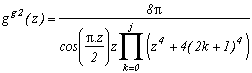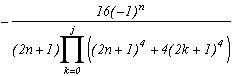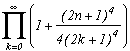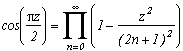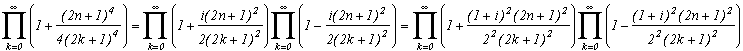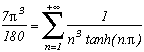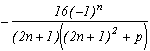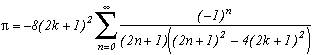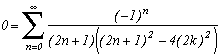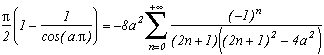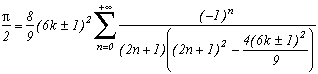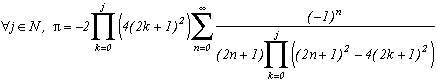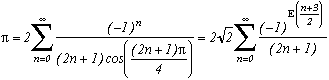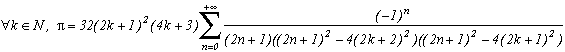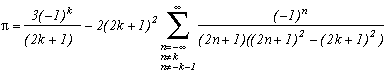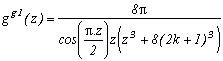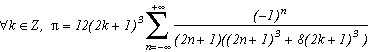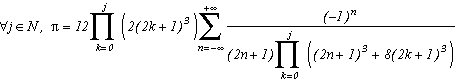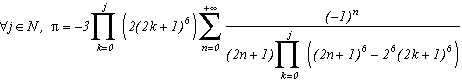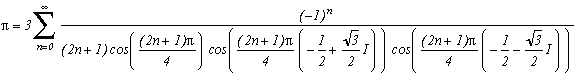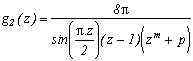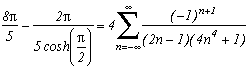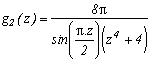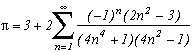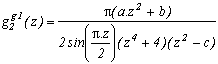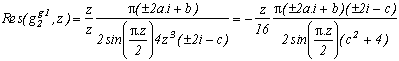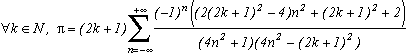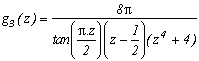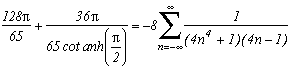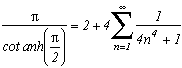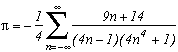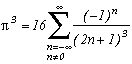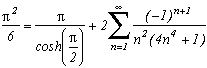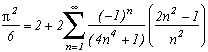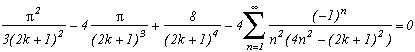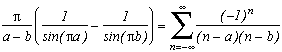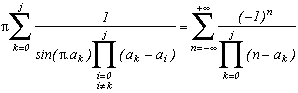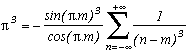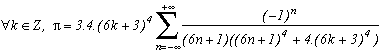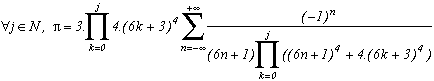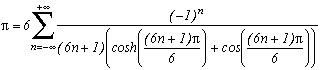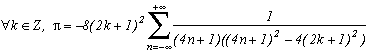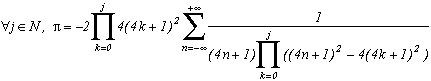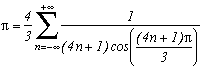Christian Frétigny

Des applications du théorème des résidus
E. Estenave / C. Fretigny

Je ne peux toutes les mettre, il y en a trop ! Vous les découvrirez au fil de la lecture de cette page. Voici néanmoins quelques exemples :

mais aussi :



...

Autour de

La première série en haut de cette page pour k=0 semble due à E. Estenave, Docteur ès Sciences, et fut publiée par son auteur avec deux démonstrations un peu confuses dans un petit livre "Sur une série servant à définir approximativement le nombre Pi" en 1901. Christian Frétigny, enseignant chercheur à l'ESPCI dans le laboratoire de physique quantique, est tombé sur ce livre dans une librairie de Paris. Il m'a d'ailleurs raconté qu'une main exigeante et anonyme avait barré au crayon le "définir" du titre et l'avait remplacé par "déterminer" avec une annotation : "Parlez français" !
Toujours est-il que C. Frétigny m'a proposé cette série et une de ses généralisations pour compléter ma collection, en me faisant part d'une autre démonstration qui utilisait le théorème des résidus. Après quelques lectures sur le sujet (je n'avais jamais étudié les fonctions holomorphes, introuvables en prépa !), nous avons engagé une petite correspondance en octobre au fur et à mesure que d'autres séries apparaissaient par la même méthode. Cette page tente de synthétiser les résultats de cette exploration, bien sûr très incomplète, vu la richesse de la méthode. Plusieurs pistes sont proposées, avec au moins un exemple pour chacune d'elle, lorsque le temps ou l'intuition ont manqué pour explorer plus profondément l'idée.
Nous ne savons d'ailleurs pas si une étude complète ou une classification existe sur le sujet, ou bien si certaines de ces séries, il est vrai peu performantes, apparaissent simplement au détour d'exercices, ni même si elles sont toutes connues (enfin, là, il ne faut peut-être pas rêver et Maple en connaît une bonne partie, d'ailleurs !). L'intérêt calculatoire n'est pas énorme, bien évidemment, et c'est d'ailleurs peut-être pourquoi je n'ai pas retrouvé ailleurs ces formules, mais la théorie, les généralisations et l'esthétique des séries sont très intéressantes. Sans compter que l'on peut redémontrer ainsi une bonne partie des formules d'Euler de façon très rapide.
A ma connaissance, et après quelques recherches, rien n'existe sur le sujet sur le web, si vous avez des renseignements, n'hésitez donc pas !

Le théorème des résidus

Tout d'abord, rappelons quelques définitions avant le fameux théorème des résidus qui sert de base à tous ces calculs :

Les fonctions holomorphes sont les fonctions de la variable complexe d'un ouvert E de C dans C, et dérivables. On se place ici dans le cadre plus général des fonctions méromorphes, rapports de deux fonctions holomorphes f(z)=g(z)/h(z), où le problème principal est que h peut s'annuler en certains z_i bien sûr. Donc soient ces fameux z_i avec iI les "pôles" de f (c'est à dire rigoureusement que pour tout i de I, il existe un n_i entier minimal, appelé l'ordre du pôle, tel que (z-z_i)ⁿⁱf(z) soit dérivable en z_i).
Le développement de Laurent général d'une fonction complexe, sur une couronne (espace entre deux cercles, pour des problèmes de convergence de la somme en + et -), est donné par :

Pour les fonctions méromorphes, la sommation est simplement finie sur les nombres négatifs, bref les a_i sont nuls pour i<(-N), N>0, N étant l'ordre du pôle z₀.
On définit le résidu de f en z_i comme le coefficient a_-1 dans le développement de Laurent de f avec z_i à la place de z₀. Lorsque z_i est un pôle simple, cela revient à calculer :

Pour un pôle d'ordre m, on a la formule un peu lourde :

Bon, jusque là, ce sont des définitions, mais que va-t-on pouvoir faire de notre fonction méromorphe qui s'ennuie un peu ?
Eh bien on considère ensuite un contour fermé G de classe C¹ contenu dans E et qui englobe les pôles z_i, iJ, JI.
On définit l'indice de G en z_i (winding number) par :

ce qui correspond en pratique au nombre de passages du contour G (compté dans le sens trigonométrique) autour du point z_i donc c'est facile à calculer pour des contours pas trop moches.
Alors, finalement, le théorème des résidus nous donne :

Intuitivement, cela veut dire que l'on peut connaître l'intégrale de f sur un contour fermé si l'on connaît le comportement de f en ses points singuliers que sont ses pôles. Ce théorème étonnant est évidemment très important en analyse complexe, et, vous allez le voir, également dans la recherche de séries tendant vers !

Application du théorème à une classe de fonctions

Dans toute la suite, les contours utilisés seront de simples contours carrés, donc l'indice de ces contours en n'importe quel point à l'intérieur sera toujours 1 d'après la définition (pratique !). Intuitivement, on a maintenant d'un côté une somme de résidus, c'est ce qui va donner les séries, et de l'autre une intégrale, que l'on espère donc calculable facilement. Pour certaines fonctions, cette intégrale est nulle lorsque l'on fait tendre le contour vers l'infini, c'est le sens de la classe de fonctions que l'on introduit ici :

Soit . On considère comme contour fermé G(N), sur lequel on va intégrer, le carré de sommets : . On évite ainsi de passer par les pôles de cotan (noté cot), c'est à dire les zéros de tan(z), c'est à dire encore les nZ (ouf..).

Montrons maintenant que l'intégrale de g sur ce contour G(N) tend vers 0 lorsque N tend vers l'infini.
Sur le montant vertical de droite, z=N+1/2+i.y, y variant de -N-1/2 à N+1/2, on a :


car
et sur le montant horizontal du haut, z=x+i(N+1/2), x variant de -N-1/2 à N+1/2, on a :

car exp((2N+1))-1>2 pour N0 et
donc, sur ces deux montants, cot(z)2, et comme cot est impaire, on en déduit que l'on a ce résultat sur tout le carré. Comme dans R, on peut alors majorer l'intégrale par la longueur de la courbe * le maximum de la fonction.
Le carré ayant pour périmètre 4*(2N+1), on obtient :

Or, pour z sur le carré, par exemple sur le montant vertical droit, on a z=(N+1/2)+iy et
z(N+1/2) (de même pour les autres montants). On peut donc encore affiner :

Faisons maintenant tendre le contour vers l'infini, c'est à dire faisons tendre N vers l'infini ou encore z vers l'infini pour z sur le contour carré. Il reste à choisir une fonction f telle que et l'intégrale tendra vers 0. Cette forme rappelle un peu le critère de Riemann pour les séries réelles, et de même, toute fonction f de la forme d'une fraction rationnelle ayant un degré du dénominateur supérieur de plus d'un au degré du numérateur conviendra. En particulier, tout f de la forme de (z^a+c)^-1 avec a>1 convient.

On a utilisé tan dans g(z) mais on peut aussi regarder du côté de sin et cos. Pour cos, pas de problème si l'on ramène 1/cos à sa forme exponentielle, puisque l'on a une somme d'exponentielles minorables au dénominateur de la même façon que pour cot.
Pour majorer 1/sin, il suffit d'utiliser la relation , puisque l'on vient de majorer cot(z) en module par 2. On peut encore utiliser les fonctions hyperboliques équivalentes (cotanh, 1/sinh, 1/cosh) mais cela semble à peu près tout.


Nous voici donc avec une intégrale qui tend vers 0 si le contour tend vers l'infini. Mais cela veut aussi dire que tous les pôles z_n de notre fonction g pour n dans I vont être contenus dans ce contour infini.
Le grand avantage est que cot(z), comme ses équivalents en 1/cos et 1/sin, admet une infinité de pôles, qui sont ici les z_n=n pour n dans Z, et la somme des résidus en ces points va donc produire une série infinie.
Après s'être occupé de l'intégrale qui est nulle, et comme l'on a vu que les indices du contour infini en les pôles z_i seront égaux à 1, notre cher théorème des résidus devient donc ici à condition de choisir f correctement :

Notre objectif, puisque les suites auront une convergence lente, est qu'au moins elles soient rationnelles. Examinons maintenant une première application afin d'observer cette méthode simple avant d'expliquer plus en détail pourquoi cela marche et d'orienter ainsi par la suite les pistes de recherche :

Exemple préliminaire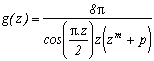

*** Cas m=4 et p=4

C'est vraiment celui qui marche le mieux, je détaille donc les calculs, ce dont je me passerai volontiers par la suite ! Il est tout d'abord clair que cette fonction rentre bien dans le cas étudié précédemment, son intégrale sur le contour infini est donc nulle.
Voyons maintenant les pôles de g et leurs résidus :
* 0 est un pôle (pour z au dénominateur), son résidu est obtenu en calculant
* Les (2n+1) pour nZ sont les pôles correspondant aux racines du cos, leurs résidus respectifs sont :




Excellent, d'un côté, on a dans le premier résidu, et de l'autre la somme des résidus en 2n+1 donne une série sur nZ plutôt sympathique !

Oui, mais voilà, il y a encore les résidus de g aux racines m-ièmes de -p qui sont aussi des pôles de g car elles annulent z^m+p. Il faudrait que leur somme soit agréable, le plus souvent nulle, ce serait parfait. Dans le cas présent les racines 4-ièmes de 4 sont 1+i,1-i, -1+i, -1-i, elles sont simples heureusement, et c'est d'ailleurs ce qui limitera les possibilités par la suite pour d'autres valeurs de m.

* Calculons les résidus en ces racines. Remarquons avant, dans le cas général, que lorsque l'on manipule une racine m-ième de p, il ne faut pas oublier que z^m=-p. Or, avec z(z^m+p) au dénominateur de g, dans le calcul du résidu de g en une racine m-ième de p, notons la a_i, on a besoin de prendre la valeur en a_i de

Donc ce terme ne dépend pas de a_i et seul le cos va en dépendre, le résidu de g en une racine m-ième de p est ainsi :
dans notre cas m=4, p=4

Mais cela, c'est une très bonne nouvelle car la somme de ces résidus est nulle. En effet, chaque résidu d'une racine s'annule avec celui de sa racine conjuguée

Il nous reste donc finalement qu'à appliquer le théorème des résidus en écrivant que la somme des résidus de g est nulle :



et finalement (ouf !)

Généralisation du cas m=4

Considérons la fonction
(g1 pour premier type de généralisation) avec k dans N (ou dans Z mais ici, (2k+1)⁴ prend les mêmes valeurs lorsque k est négatif à cause de la puissance 4)

Ici et par la suite, j'userai d'un petit tableau pour présenter les pôles et leurs résidus, c'est tout de même plus clair que si les résultats sont noyés au milieu du texte. De plus, seule la somme des résidus des racines est importante pour la calcul, pas le résidu en une racine, sauf cas particulier, puisque l'on sait que c'est à cause du sinus que la somme s'annule. J'omettrai donc souvent par la suite l'expression du résidu seul en une racine, surtout lors des généralisations, le résultat étant assez pénible !

Pôles	Résidus
0
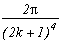
(2n+1)
+/-(2k+1)+/-i(2k+1)
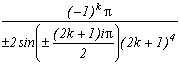
somme des résidus des racines	0

Ce qui permet de même que précédemment de construire la série suivante :

Notons que si l'on fait tendre k vers l'infini, le rapport du terme devant la somme et de celui au dénominateur tend vers 4, et l'on retrouve la suite de Leibniz ! Bon, la rigueur est un peu oubliée puisque l'on n'a pas justifié le passage à la limite, mais la remarque valait surtout pour l'intuitivité du résultat.


Augmentation du degré du dénominateur

Plus fort !
Le degré du dénominateur, hormis le z, est de 4 avec le z⁴+4. Eh bien, on peut l'augmenter pour faire converger la suite plus vite.
Considérons ainsi la fonction :


Calculons les résidus :

Pôles	Résidus
0
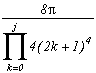
(2n+1)
somme des résidus des racines	0

On obtient alors la série :



On peut s'intéresser au cas limite lorsque j tend vers l'infini, cela revient à calculer le produit infini :
On peut partir pour cela de l'expression bien connue (voir par exemple l'encyclopédie d'Eric Weisstein) :

Cela est tout à fait intuitif, puisque le produit infini s'annule dès que z prend une valeur impaire, donc c'est une fonction (2n+1) périodique, cela doit être le cosinus... On a donc :




et finalement :

Bien évidemment, cela n'a plus guère d'intérêt pour le calcul des décimales et là encore la rigueur est un peu oubliée, mais la formule est assez esthétique, n'est-ce-pas ?
A noter que je pense que l'on peut la rapprocher des identités sur la fonction de Riemann trouvées par Simon Plouffe et les Borwein en 1997/1998 (voir sa page perso). Une identité utilisée est en effet la somme

La démonstration en est donnée sur la page de ce site consacrée à Plouffe et d'autres formules du même type s'y trouvent.

Alors, pourquoi ça marche et comment continuer ?

Le point majeur à étudier est celui de la forme des racines m-ièmes de p. On a vu que l'annulation de la somme des résidus pour ces racines dépend de la transformation du cosinus en sin à cause du fait que sin est impaire. Comme l'on part d'un cosinus, il faut donc qu'il y ait une translation de car cos(x)=+/-sin(x).
Dans l'exemple précédent, comme l'on part de cos(z/2), il suffit que lors du calcul des résidus, la racine m-ième de p ait une partie réelle de la forme (2k+1), donc entière et impaire. C'était bien la cas précédemment pour m=4 et p=4 puisque les racines sont les +/-1+/-i.

Cette propriété dépend essentiellement du degré de la puissance m au travers de la forme des racines m-ièmes de l'unité. Pour trouver les racines de z^m+p, il suffit en effet simplement de multiplier les racines m-ièmes de l'unité par p^1/m.
Si on note a_k la partie réelle de la k-ième racine m-ième de l'unité, une condition suffisante pour que cela marche est donc qu'il existe p entier tel que

a_k.p^1/m=(2k+1)

et que cela soit valable pour toutes les racines avec le même p.
On le verra par la suite, seuls m=2, m=3, m=4 et m=6 semblent convenir, car au dessus du degré 6, par exemple pour le degré 8 qui semble favorable, on trouve un p pour 4 racines et un autre p pour les 4 autres racines, et plus rien ne marche, il y a constamment un décalage de 2^1/2 ! Notons aussi que, pour profiter d'un entier solution, on s'intéressera parfois en pratique plutôt à z^m+/-q^m.

Et la généralisation - pourquoi ça marche ?

Lorsque le degré m marche et que l'on a trouvé p, rien n'empêche ensuite de multiplier p par (2k+1)^m, on sait que l'on multiplie alors les racines m-ièmes de p par (2k+1), mais puisque leur partie réelle est impaire et que le produit de deux impairs est impair, les nouvelles racines ont encore la bonne propriété sur leur partie réelle. Cela explique pourquoi la généralisation de l'exemple préliminaire fonctionne.
Il n'est pas interdit aussi de disposer au dénominateur autant de polynômes de la forme z^m+p(2k+1)^m que l'on veut. Cela crée des produits qui augmentent le degré du dénominateur et aboutissent à des cas limites comme on l'a vu.

Voilà en bref le principe d'exploration, il n'est pas impossible que des cas particuliers ne rentrant pas dans les hypothèses ci-dessus apparaissent, mais aucun n'a encore montré le bout de son nez. Tous les exemples suivants sont donc des variantes de ce principe. Voici les diverses pistes qui ont été envisagées :

Piste 1 : utilisation du cos, de z et d'un autre polynôme de degré m : z^m+p, m>1 soit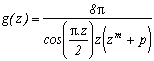

*** Cas m=4 et p=4

Celui-là, on l'a donc vu comme exemple préliminaire

*** Cas m=2

* p=-4(2k+1)², p=-4(2k)², p=-4(6k+/-1)²/3

m=2 est un cas un peu particulier, la simplicité des racines nous permet d'étudier le cas général en laissant initialement p comme paramètre dans g. On va retrouver ainsi naturellement les valeurs de p choisies ci-dessus :

Voici donc le tableau rituel :

Pôles	Résidus
0
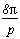
(2n+1)
somme des résidus des racines

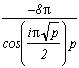
Le i dans le cosinus est très gênant si l'on veut une relation agréable et ne pas tomber sur des cosh du plus mauvais effet. Il suffit pour l'enlever de prendre p négatif, un autre i sortira de la racine.
Bien, ensuite, il s'agit de ne pas annuler le cosinus au dénominateur, il faut donc qu'il y ait un facteur 4 sous la racine pour tomber sur des cosinus de multiples de dont on connait bien la valeur.
Finalement, on peut prendre pour valeur de p soit -4(2k+1)² soit -4(2k)². Et ce choix est loin d'être anodin, voyons plutôt :

Avec p=-4(2k+1)² , on obtient pour k entier, toujours en annulant la somme des résidus ci-dessus :

Mais avec p=-4(2k)² , surprise, on obtient :

car le résidu en 0 s'annule avec ceux des racines puisque cos(2k)=1.
Donc selon que l'on choisit les impairs 2k+1 ou les pairs 2k, on a une somme égale à ou nulle, voilà un phénomène intéressant !
En fait, plus généralement, si l'on choisit p=-4a², on obtient d'après le tableau des résidus le joli résultat suivant, qui explique cette curiosité :

La seule autre valeur rationnelle pour le cosinus concerne la valeur a=(6k+/-1)/3, ce qui donne la nouvelle série :

Augmentation du degré du dénominateur

cela donne :


et pour le cas limite en faisant tendre j vers l'infini :

Cette dernière série est déjà citée d'après C. Frétigny dans Gradshteyn, I.S. and Ryzhik, I.M. " Tables of Integrals, Series, and Products " San Diego, CA: Academic Press, 1996 (en version CD)
Je n'ai malheureusement pas ce livre ni le CD, mais je sens qu'ils me plairaient !

Il n'y a pas de cas limite pour la deuxième série nulle, on tombe sur la somme des (-1)ⁿ dont le résultat, si il est normalement indéterminable, correspond intuitivement bien à la valeur 0 de la série initiale.

On peut augmenter le degré du dénominateur de façon plus exotique. Comme l'on a trouvé une série de somme nulle, on peut la soustraire de la série donnant Pi pour trouver une nouvelle série (bricolage !). Ainsi, on a :

* p=-(2k+1)²

Il y a cet autre cas intéressant pour m=2. Il correspond au cas où l'on sait que le dénominateur va s'annuler pour la valeur n=k puisque l'on va avoir (2n+1)²-(2k+1)² dans la série. L'ordre des pôles en z=+/-(2k+1) n'est alors plus 1. Mais il suffit de calculer les résidus en ces valeurs avec la formule différentielle proposée dans la section "Théorème des résidus", et les résidus pour les autres valeurs 2n+1 de façon classique, cela donne :

Pôles	Résidus
0
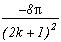
(2n+1) (n#k)
+/-(2k+1)

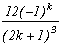
En annulant la somme de ces résidus, on peut alors écrire pour tout k entier :

La généralisation par l'augmentation de degré au dénominateur semble plus complexe tout simplement parce que cela oblige à retirer d'autres valeurs de n de la série. On voit en tous les cas qu'il n'existe pas de cas limite (car il ne resterait plus de valeurs de n dans la série !!)

*** Cas m=3 et p=2³

Un cas très classique, parfaitement ressemblant au cas m=4, et facilement généralisable, c'est d'ailleurs par là que l'on va commencer puisque le cas p=8 correspond à k=0 dans la généralisation :
Rappelons la fonction utilisée pour cette généralisation :



Voici le tableau des pôles/résidus :

Pôles	Résidus
0
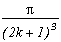
(2n+1)
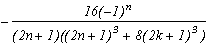
-2-4k (1ère racine)
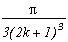
1+2k+/-I(2k+1)31/2 (la somme des résidus s'annule)

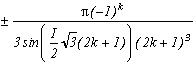
On le voit, la seule particularité de ce cas est d'avoir une première racine indépendante des autres (à cause du degré 3), mais son résidu est parfaitement utilisable, et l'on peut former la somme (qui était assez prévisible !) :

Une petite variante tout de même, la somme se fait cette fois-ci sur Z, toujours à cause du degré 3, la somme sur N n'étant plus égale à la somme sur Z^-. Je pense que c'est aussi pour cela qu'il ne suffit plus de faire tendre k vers l'infini pour retrouver la suite de Leibniz comme tout à l'heure pour le cas m=2.
Cependant, si l'on combine les sommes sur Z^- et Z⁺, on arrive tout de même à obtenir une série sur N qui est exactement celle présentée dans la section suivante "Cas m=6 et p=-2⁶"


Augmentation du degré du dénominateur

Le principe est connu maintenant, évitons de charger inutilement cette page déjà très longue. On peut sans peine appliquer le même processu que pour m=2 ou m=4, on obtient pout tout j entier :

Le cas limite ne semble pas calculable aisément à cause du produit infini (est-il seulement calculable ?), si quelqu'un a un résultat... Tout ce que l'on peut dire est que c'est une fonction (2n+1) périodique sur R⁺ et non sur R^-. Cela rappelle un peu les problèmes concernant la somme des inverses des puissances impaires, c'est à dire la fonction zêta pour les valeurs impaires.

*** Cas m=6 et p=-2⁶

Dernière valeur apparemment possible, ce cas ne pose pas de difficultés particulières théoriques. Les racines au degré 6 sont :
+/-(2+4k) qui donnent comme au degré 3 un multiple de Pi
+/-(2+4k){j, j²} qui ont une partie réelle impaire, donc le cosinus se transforme comme d'habitude en sin et les résidus des racines conjuguées s'annulent.

On passe donc vite, pour filer sur le tableau des pôles/résidus et sur les résultats :

Pôles	Résidus
0
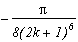
(2n+1)
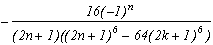
somme des résidus des racines	0

Cela donne :

Augmentation du degré du dénominateur

Pas de problèmes non plus ici, on obtient facilement :

Pour le cas limite, on utilise le même procédé que pour m=4, à savoir l'utilisation du produit infini de degré 2 valant cos(z/2). La lourdeur des calculs et la taille (déjà conséquente !) de cette page faisant, on va éviter de détailler le calcul. Pour obtenir le produit infini de degré 6, on va multiplier trois fois ce produit infini de degré 2 valant cos, avec z=(n+1/2), z=j.(n+1/2) et z=j²(n+1/2). On trouve alors :


Les I vont donner des cosh en développant, (mais ce n'est pas très beau, mieux vaut laisser sous forme compacte) ce qui va assurer une convergence rapide.

Piste 2 : utilisation du sin, et d'un autre polynôme de degré m : z^m+p, m>1 :

Comme on a obtenu des séries "impaires" avec le cosinus, c'est à dire avec un (2n+1) au dénominateur du terme général de la série, on pourrait s'attendre à obtenir des séries paires avec le sinus. Mais malheureusement, tout ne marche pas aussi bien...
En effet, contrairement au cas (2n+1), 0 est un cas particulier de 2n, et le résidu en 0
est alors plus difficile à calculer, il est en fait nul, mince, n'apparaît plus...
Il faut recourir à une astuce, et décaler le z du dénominateur en z-1, c'est à dire considérer la fonction
Le 1 est choisi pour obtenir une valeur agréable du sinus, mais l'on pourrait partir d'un autre décalage, pourvu qu'il ne soit pas de la forme 2n.
Tout cela est bien joli, mais avec l'habitude de cette méthode, on voit immédiatement que ce décalage va ruiner nos espoirs de trouver des séries paires avec cette piste puisque l'on aura au dénominateur une chose de la forme q.n-a. Terrible...

*** Cas m=4 et p=4

Un gros problème avec ce cas, le décalage empêche la somme des résidus des racines de s'annuler totalement et l'on voit apparaître des cosh du plus mauvais effet...
Voyons ainsi le tableau des pôles/résidus :

Pôles	Résidus
1
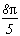
2n
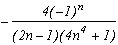
somme des résidus des racines +/-1+/-i

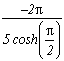
Ce qui donne la série :

Il faut absolument se débarrasser du terme en cosh, sinon, la série n'a pas vraiment d'intérêt...
Une solution est d'écrire ce terme sous forme d'une série par la même méthode des résidus, puis de rassembler les deux séries.
Ainsi, on considère :

Avec la méthode habituelle, les résidus en 2n et la somme de ceux-ci pour les racines donnent la série :

Au passage, notez l'extraordinaire pureté de la série à droite, d'une simplicité exceptionnelle, et l'horreur du terme de gauche ! La forme du membre de gauche aurait-elle des propriétés si remarquables pour être égal à ce genre de série ?

Toujours est-il qu'en regroupant les deux équations précédentes, on trouve :

Encore une jolie série, mais peut-on en tirer un résultat encore plus satisfaisant ?

Généralisation

Comment la généraliser ? Pas de la manière habituelle avec les (2k+1), on va tenter d'être plus précis en introduisant la fonction :

Nous allons chercher la condition sur a, b, et c pour que la somme des résidus des racines de z⁴+4 s'annule.
Pour cela, voyons le calcul des résidus en z=1+/-i (en n'oubliant pas que z²=+/-2i et z⁴=-4)

Bon, on sait que z²=+/-2i donc, pour que la somme de ces deux résidus s'annule, il suffit d'utiliser cette propriété et que le terme derrière le z au numérateur soit donc proportionnel à z, c'est à dire :

(+/-2a.i+b)(+/-2i-c)=4a-b.c+/-2i(a.c+b)=1+/-i

La série considérée précédemment correspond à a=1, b=-6 et c=1
La somme des deux autres résidus s'annule car le carré des racines est réel (+/-2).

Intéressons-nous maintenant aux autres pôles, et sommons par le théorème des résidus comme d'habitude. Pour 2n, calcul classique que je n'expose pas.
Comme la somme des résidus pour les racines de z²-c donne , on a tout intérêt à choisir c=(2k+1)² pour que le sinus soit égal à 1, ce qui donne après de nombreuses simplifications (ouf !):

La formule originelle est le cas k=0.

Pour autant qu'elle marche, cette méthode n'est pas vraiment faîte pour les généralisations et dépend surtout des propriétés de la fonction. Ici, le degré 4 est idéal car les racines 1+/-i ont pour carré +/-2i, ce qui permet l'annulation des résidus des racines conjuguées de z⁴+4.

Les degrés 2, 3 et 8 ne m'ont pas semblé favorables, mais il y a donc certainement beaucoup encore à fouiller de ce côté-ci !

Piste 3 : utilisation de tan et d'un autre polynôme de degré m : z^m+p, m>1

Intuitivement, la dérivée de tan : (1+tan²) fait penser que l'on peut obtenir des séries non alternées, contrairement aux sinus et aux cosinus. Car le (-1)ⁿ venait de l'expression de la dérivée de cos et sin en (2n+1) ou (2n). L'utilisation de la tangente est tout à fait similaire à celle du sinus, car leurs comportements sont équivalents à l'origine (notamment les pôles sont les mêmes). Dès lors, on va être confronté au même problème que pour le sinus, et l'on va devoir décaler z en z-1/2 cette fois-ci (pour tan(/4)=1) pour éviter d'avoir un résidu nul en 0.

*** Cas m=4 et p=4

De même que pour le sinus, c'est le degré 4 qui semble marcher le mieux pour les mêmes raisons. Passons donc vite et courons vers les résultats !
En considérant :

on obtient le tableau des pôles/résidus suivant :

Pôles	Résidus
1/2
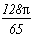
2n
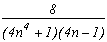
somme des résidus des racines +/-1+/-i

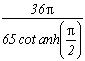
et la série :

Ensuite, l'étude de la même fonction g₃ sans le z-1/2 conduit à la jolie expression :

ce qui, injecté dans la série précédente, donne :

Je n'ai pas encore réussi à généraliser le résultat... et je n'ai pas essayé avec d'autres degrés que 4. Avis aux amateurs !
Notez que par rapport aux séries habituelles, on a cette fois-ci 4n-1 au lieu de 2n+/-1. Cette recherche d'autres a*n+/-1 sera l'objet de la piste 6.

Piste 4 : utilisation de z^q et d'un autre polynôme de degré m : z^m+p, m>1 :

*** Sans polynôme z^m+p

On considèrera tout d'abord les fonctions sans polynôme de degré m, c'est à dire du type : ou encore avec le cosinus ou la tangente.
Ces fonctions servent à redémontrer les innombrables formules d'Euler/Bernoulli. On calculera les résidus en 0 avec la formule différentielle de la section "Théorème des résidus" pour un pôle d'ordre m.
Une chose à remarquer simplement est que la somme sur Z (privé de 0 lorsqu'il le faut, bien sûr) des inverses des puissances est nulle pour certaines puissances à cause de la parité. Ainsi, c'est ce qui explique que pour le sinus et q=2, le résidu en 0 n'est pas nul et vaut alors qu'il l'est pour q=3. En effet, on a . Et donc - maintenant que l'on est habitué, on peut même se passer du tableau des pôles/résidus - q=2 donne :

Plus généralement, pour le sinus, on peut utiliser les puissances q=2k pour donner des séries du type de la précédente. La tangente utilise aussi q=2k et donne les séries non alternées.
Pour le cosinus, c'est évidemment le même phénomène décalé puisque 0 n'est pas un pôle du cosinus. On doit donc utiliser q=2k+1 pour trouver la somme des inverses des puissances des impairs. Ainsi, q=3 donne :

Ce qui est rageant, c'est que le phénomène est la raison pour laquelle on ne peut pas calculer avec cette méthode la valeur de (3), la constante d'Apéry. Et cela est valable pour toutes les puissances impaires, sauf pour les séries alternées comme ci-dessus, malheureusement, on ne peut pas passer d'une série alternée à une non alternée avec les impairs contrairement aux pairs. L'un des plus importants problèmes mathématiques contemporains tient à peu de choses tout de même...

*** Avec polynôme z^m+p

Malheureusement, tout marche beaucoup moins bien ici que lorsque q=1 (z seulement). La somme des résidus des racines ne s'annule plus par exemple dans le si joli cas m=4 et p=4 même avec le cosinus. On obtient une variété hyperbolique genre cosh/sinh et il faut user encore de l'astuce comme pour les sinus, c'est à dire utiliser une expression de cosh/sinh pour la remplacer dans la série.
Mais un autre problème arrive : cette expression, par exemple ne converge pas aussi vite que celle que l'on a obtenue dans la série car on y fait varier la puissance de (2n+1)^q, expression absente dans la série avec cosh. Et donc impossible de s'en sortir pour obtenir un gain de vitesse grâce au (2n+1)^q.
Par exemple, en considérant pour q=2, m=4 et p=4 et le sinus :
on obtient l'expression :

et l'expression de cosh au dessus permet d'obtenir la série :

Mais ce n'est guère réjouissant, et semble difficile à généraliser.


Pour certaines puissances q, on arrive à annuler la somme des résidus des racines de z⁴+4 (pour le cosinus et q=5 par exemple) mais comme décidément ça ne veut pas marcher, le résidu en 0 est 1/192*(5⁴-96) et on ne peut isoler dans cette expression car le polynôme correspondant 1/192*x(5x⁴-96)=c n'a pas de racines exprimables sous la forme de radicaux...

Pour le degré q=2, on a un peu le même problème dans la mesure ou l'on obtient la série dans un polynôme du second degré de variable . Mais si l'on isole , des racines carrés arrivent or, l'objectif premier était de rester dans les séries rationnelles, donc également sans racines. Avoir une série de somme ² comme au dessus passe encore, mais si l'on commence à introduire des racines, cette page aura une longueur tendant franchement vers l'infini !
Je donne donc seulement un exemple de ce que l'on peut obtenir :
q=2, m=2, p=(2k+1)² donne :

Donc, on en reste là avec cette piste qui semble un peu bloquée si l'on s'en tient à l'optique originelle.

Piste 5 : utilisation de pôles décalés pour les polynômes

Cette méthode est très riche pour obtenir de jolies formules généralisées.Elle consiste à prendre au lieu du z un z-a systématiquement, étant entendu que l'on peut rajouter ensuite plusieurs autres polynômes au dénominateur. Pour la rapidité du chargement de la page (mais quelqu'un sera-t-il seulement parvenu jusque là ??), j'omets les détails du calcul, lorsqu'il est très classique.

Exemple 1 : deux pôles simples décalés
L'étude de donne :

Et en faisant tendre a vers b, puis b vers 0, on retrouve bien la série d'Euler (encore heureux !)
Les tan et cos (pris en z/2) donnent exactement le même type de formule avec les caractéristiques de chacun : tan à la place du sin et série non alternée pour la tan, et cos à la place de sin et 2n+1 à la place de n pour le cosinus
Le résultat est assez facilement généralisable pour j+1 pôles distincts au dénominateur et cela donne :

Malheureusement, comme les seules valeurs rationnelles pour le sinus sont prises pour des a_k rationnels en /3 et /2, dans le cadre de l'étude, on ne peut avoir plus de deux termes dans le produit et donc aller au delà de j=1.

Exemple 2 : un pôle d'ordre q décalé

On va prendre q=3 ici, car il n'existe pas semble-t-il de cas vraiment général, les calculs dépendent de la puissance utilisée. Considérons ainsi la fonction . L'application de la méthode des résidus donne :

si je ne me suis pas trompé. Les cas m=1/3 ou m=1/2 semblent les plus intéressants (et ce sont visiblement les seuls) si l'on veut obtenir une expression sans terme irrationnel (hormis bien sûr !).
On peut aussi choisir tan à la place de sin. On obtient :

Piste 6 : utilisation d'un polynôme z^m+p, et recherche de coefficients a.n+/-1 au dénominateur de la série

Cette piste a été effleurée à la fin de la piste 3. Deux méthodes sont utilisables pour y arriver :
* soit l'on utilise un décalage général (z+/-b) et l'on regarde ensuite quelles valeurs de b (de la forme 1/r) permettent de changer le 2n+/-b en 2r.n+/1.
*soit l'on part d'un décalage à l'intérieur du cos/sin c'est à dire c..z+d, de façon à ce que les pôles soient directement de la forme a.n+1.

Les deux cas sont clairements équivalents car ils correspondent à un décalage tous les deux, le second est plus pratique pour trouver ce qui marche et former les séries.
Donc, si l'on se penche sur la seconde méthode, et que l'on se base toujours sur l'annulation des résidus des pôles de z^m+p, fixons les notations, et recherchons a.n+1 au dénominateur avec cos(b.z+c.) c'est à dire la fonction .
Voyons les contraintes :

1. Comme on a z au dénominateur, 0 est un pôle et il faut donc que le résidu en ce pôle, c'est à dire en fait cos(c.) soit rationnel (pas de problème pour la rationnalité de p !). Cela donne la condition (1) :

(1)

On exclut le cas c=1/2 qui donne un pôle de cosinus (pas pratique !)

2. a.n+1 doit être un pôle, donc b..(a.n+1)+c.=(2n+1)/2 ce qui est équivalent à la condition (2) :

a.b=1 (2a)
b+c=1/2 (2b)

3. Enfin, pour qu'il y ait transformation du cosinus en sinus, la partie réelle z₁ de z se doit de vérifier la condition (3) valable pour les généralisations :

(3)

Résolvons ce sytème en utilisant les différentes valeurs possibles de c :
A noter que c=0 est le cas que l'on a étudié dans les pistes précédentes
cela donne

c	c=0	c=1/3	c=-1/3	c=2/3	c=-2/3
b	b=1/2	b=1/6	b=5/6	b=-1/6	b=7/6
a	a=2	a=6	a=6/5	a=-6	a=6/7
z1	2k+1	6k+1	(6k+1)/5	1-6k	(6k+1)/7
Valeurs de a.n+1 possibles	2n+1	6n+1	6n+5~6n-1	1-6n~6n-1	6n+7~6n+1

Tout est clair à présent ! Encore une remarque tout de même, la forme de z₁ oblige à considéréer seulement un degré 2, voire 3. En effet, 4 racines ne peuvent avoir la même partie réelle. On verra pourtant qu'il existe un cas particulier pour le degré 4.
Mais restons pour l'instant dans l'application du tableau, après avoir débroussaillé, c'est assez facile.

Considérons ainsi l'exemple du degré 3 avec c=1/3 et b=1/6 (3è colonne du tableau) :

donne la série :

Hélas, pas d'augmentation du degré du dénominateur à cause du degré 3, comme on l'avait vu à la piste 1...

Il existe sinon un cas particulier, le degré 4. La forme obligatoire de z₁ vue ci-dessus empêche aux résidus des racines 4-ièmes conjuguées de z⁴+4 de s'annuler deux à deux. Mais la somme des quatre résidus est nulle ! Je ne crois pas que ce phénomène se retrouve à un degré supérieur, cela est dû à la symétrie parfaite des racines pour le degré 4, c'est dommage...
Toujours est-il qu'en considérant p=4*(6k+3)⁴, et encore c=1/3 et b=1/6, on obtient la série suivante :

Et en augmentant le degré du dénominateur, on trouve :

Et comme cas limite, on a :

L'étude du sinus est équivalent à celle du cosinus par translation de /2, donc, on ne trouvera pas de nouvelles séries par là.
Avec la tangente, la seule possibilité de tangente rationnelle non nulle est pour :
tan(/4)=1. En suivant le même raisonnement que pour le cosinus, on trouve tout naturellement une série en 4n+1, ici pour le degré 2, qui semble le seul possible :

On peut augmenter le degré du dénominateur et obtenir :

et le cas limite donne :

D'autres pistes ?

Avec cette méthode, on voit que l'on peut redémontrer nombre de formules, et bien sûr, toutes ne sont pas là !
On peut chercher d'autres fonctions à mettre au dénominateur des fonctions g. Par exemple, on peut mettre l'exponentielle complexe à la place des cosinus/sinus etc... Seule problème, l'exponentielle ne s'annule pas, il faut donc la coupler avec un cosinus.
Plus généralement, on ne peut utiliser de fonctions qui ne sont pas définies correctement sur tout le domaine complexe. Par exemple, on ne peut utiliser cos(*log) pour obtenir des séries à la Simon Plouffe car le logarithme n'est défini dans le domaine complexe que si l'on effectue une coupure (suppression d'une demi-droite issue de l'origine) dans le domaine de définition complexe. Sinon, on pourrait tourner autour et avoir deux valeurs différentes pour z et z*exp(2i) (log(z) et log(z)+2i). Ce qui serait pour le moins gênant !

A part les polynômes, je n'ai pas d'autres idées d'application pour l'instant, faîtes m'en part si vous en avez !