Eugène Salamin / Richard Brent

1) Formule originelle Brent/Salamin 1976 (Mathématics of computation )



2) Suite assez évidente que je n'ai bizarrement trouvée nulle part !



3) Variation des frères Borwein 1984



4) Frères Borwein 1987 ( Pi and the AGM )

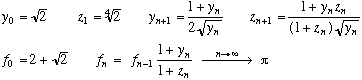
Une autre suite d'après une observation de Salamin

Je n'ai pas encore testé ces algorithmes.

Convergence quadratique



Convergence cubique

Cet algorithme converge vers le plus proche multiple de Pi de f₀.

f_n=f_n-1+sin(f_n-1)

Je n'ai malheureusement pas trouvé les démonstrations de ces algorithmes...

Tranches de vie

Et je n'ai pas trouvé grand-chose non plus sur Salamin ou très peu... comme cette photo le montrant en compagnie des plus grands chercheurs sur Pi (Bailey, Gosper, Kanada...)
Sur Brent, par contre, tout va bien ! Richard Brent est un mathématicien australien né en 1946. Il est pour l'instant professeur à Oxford et est spécialiste des algorithmes. Pour plus de renseignements, vous pouvez allez visiter sa page personnelle.

Autour de

La formule originelle a été découverte en 1973 et publiée en 1976 par Eugène Salamin dans l'article Computation of Pi dans la revue Mathematics of computation . Elle fut publiée au même moment et indépendamment par Richard Brent également (qui est d'ailleurs maintenant directeur de Mathematics of computation !). Il est vrai que la coutume est de l'appeler algorithme de Salamin, mais n'oublions pas ce cher Brent !
Cette formule est la première véritable découverte importante concernant le calcul de Pi depuis les formules d'arctan et celles de Ramanujan. La force de cet algorithme est de proposer une convergence quadratique (2ⁿ comme je le note habituellement sur ce site) c'est à dire que le nombre de décimales exactes double à chaque itération ! Une fusée !
Bien sûr, la démonstration est à la hauteur de la performance, d'une longueur très pénible... Mais j'ai passé un tel temps vainement sur Internet à la recherche de cette démonstration lorsque j'en avais besoin pour mon dossier sur Pi (voir page perso) que je ne peux résister à la publier ici...
Elle repose sur la moyenne arithmético-géométrique qui fut étudiée par Legendre et Gauss, mais ce dernier, pour une fois (!), ne vit pas l'intérêt qu'elle pouvait avoir pour le calcul de Pi !

Démonstration

C'est parti pour les algorithmes 1), 2) et 4) ! Je vais tenter de bien structurer l'affichage des résultats car le web n'est pas ce qu'il y a de plus pratique pour des démonstrations mathématiques!

Moyenne arithmético-géométrique

Soient a et b deux réels positifs ou nuls. On définit les suites (a_n) et (b_n) par :

I Convergence

Lemme 1 : (an) et (bn) sont convergentes et de même limite. De plus, (an) est décroissante et (bn) est croissante. Cette limite est notée M(a,b) et appelée Moyenne arithmético-géométrique de a et b.

Démonstration

I.a) Montrons que pour n>0 et a#b,

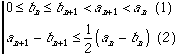
• En effet, si a=b, on a immédiatement pour tout n entier a_n=a=b_n
  
  
• Si a=0 ou b=0, on a (tout aussi immédiatement !) pour tout entier n b_n=0 et a_n+1=a_n/2 ce qui assure bien (1) et (2)
  
  
• Si a>0 et b>0, a#b

I.a).(1) Une petite récurrence pour (1) pour bien commencer !
n=1 : a#b donc en développant, donc b₁<a₁, et en refaisant de même, b₂<a₂.
De plus, a₂=a₁ /2+b₁ /2<a₁ /2+a₁ /2=a₁ donc a₂<a₁ et b₂>(b₁²)^1/2=b₁ donc, finalement, on a le résultat (1) au rang 1

Supposons maintenant le résultat (1) valable pour k dans [[1,n]]...
Puisque b_n<a_n, on a de même (a_nb_n)^1/2<(a_n+b_n)/2 donc b_n+1<a_n+1 et a_n+1<2a_n/2=a_n et enfin b_n+1>(b_n²)^1/2=b_n
Donc 0<b_n<b_n+1<a_n+1<a_n
C'est sacrément l'hypothèse au rang suivant, donc par le théorème de récurrence, le résultat (1) est bien valable pour tout entier n non nul...

I.a).(2) Pour tout n>0, on a :

C'est bien le résultat (2) !

---

I.b) Montrons maintenant que ces suites sont convergentes :

• Si a=b on a pour tout n a_n=b_n et donc (difficile !) a_n=a=b_n
• Si b=0, a#0 on a pour tout n>0 : b_n=0 et a_n=a_n-1 /2=a₀ /2ⁿ donc a_n=b_n=0
• Si a=0, a_n=0 et donc b_n=0 pour tout n, ce qui règle l'affaire de la limite !
• Si a>0, b>0, a#b
  _ D'après I a) (1) (b_n) est croissante, et (a_n) est décroissante
  _ De plus, d'après I a) (2) et par récurrence immédiate, a_n-b_n<(a₁-b₁)/2^n-1 donc (a_n-b_n)=0, tiens !
  Ne serait-ce pas des suites adjacentes ? Mais oui ! Elles convergent alors vers une même limite que nous noterons donc M(a,b)

---

II Propriétés de la moyenne AGM (arithmético-géométrique)

II.a) M(an,bn)=M(a,b) II.b) M(a,b)=M(b,a) II.c) M(ßa,ßb)=ßM(a,b) pour n entier, ß>0, a>0, b>0

Démonstration

II.a) Soit n₀>0
(a_no+k)_k et (b_no+k)_k ont même limite que (a_k)_k et (b_k)_k donc, M(a_no,b_no)=M(a,b)

II.b) Soient (a'_n) et (b'_n) les suites définies comme (a_n) et (b_n), mais avec a'₀=b et b'₀=a
On a a'₁=a₁ et b'₁=b₁ donc d'après I. a) avec n=1, on a M(a,b)=M(b,a)

II.c) De même, si on définit (a"_n) et (b"_n) par a"₀=ßa₀ et b"₀=ßb₀, on a immédiatement pour tout n : a"_n=ßa_n et b"_n=ßb_n.
Donc, en passant à la limite, M(ßa,ßb)=ßM(a,b)

---

III Fonction f(x)=M(1,x)

Nous voici au coeur de la démonstration : Pour a=1 et b=x, les résultats précédents (convergence...) nous permettent de construire une fonction f définie par :
pour x réel positif ou nul,

f(x)=M(1,x)

Les résultats intéressants sur cette fonction sont :

III.a) Lemme 2

f est continue sur [0,+[

Démonstration

Dans le cas a₀=a=1 et b₀=b=x, nous allons montrer la convergence uniforme des suites (a_n) et (b_n) sur tout compact de R⁺ vers la fonction f. Pour bien différencier ce cas de l'étude précédente, je noterai respectivement (U_n) et (V_n) ces suites de fonctions...

III.a).1) Montrons que pour tout n entier, U_n et V_n sont continues sur R⁺

Par récurrence, par exemple !
n=0 : U₀(x)=1, V₀(x)=x, no comment !
Supposons le résultat jusqu'à un certain n entier,
U_n+1=(U_n+V_n)/2 et V_n+1=(U_nV_n)^1/2 donc U_n+1 et V_n+1 sont clairement continues comme composées de fonctions continues...
Le théorème de récurrence se vérifie donc, U_n et V_n sont continues pour tout n sur R⁺.

---

III.a).2) Montrons la convergence uniforme de U_n et V_n vers f sur tout compact de R⁺ :

• D'après I.a).1). on a n0, b_nM(a,b)a_n donc :
  xR⁺, V_n(x)f(x)U_n(x) donc :
  
  0U_n(x)-f(x)U_n(x)-V_n(x)<(U_n-1(x)-V_n-1(x))/2<|1-x|.2^-n pour tout xR⁺
  
  
• Plaçons nous sur un compact [A,B] de R⁺
  nN*, 0U_n(x)-f(x)(B+1)2^-n
  
  De même, 0f(x)-V_n(x)U_n(x)-V_n(x)<|1-x|2^-n(B+1).2^-n

Cette majoration est uniforme, il y a donc convergence uniforme de (U_n) et (V_n) vers la fonction f sur tout compact de R⁺

Donc f est continue sur [0,+[, déja un premier résultat très important !

---

III.b) Lemme 3

f est croissante sur [0,+[

Démonstration

III.b).1) Montrons par récurrence (encore !) sur nN que (Un) et (Vn) sont croissantes sur [0,+[
U₀=1 et V₀=x donc on a le résultat pour n=0
Supposons que le résultat soit valable pour un certain nN
U_n et V_n étant croissantes, U_n+V_n et (U_nV_n)^1/2 aussi donc U_n+1 et V_n+1 le sont également et c'est l'hypothèse au rang suivant !
Le résultat est bien valable pour tout nN.

---

III.b).2). Soient x₁0, x₂0 avec x₁<x₂
Puisqu'il y a convergence uniforme de (U_n) vers f, on a f(x₂)-f(x₁)=(U_n(x₂)-U_n(x₁))
or nN*, U_n(x₂)-U_n(x₁)0 (croissance de U_n), donc f(x₂)-f(x₁)0, ce qui nous assure la croissance de f sur [0,+[, et voilà, fin de la démonstration du lemme 3 !

---

III.c) Lemme 4 (Etude aux bornes...)

f admet une tangente verticale en x=0 En 0, lim f =0 En +, lim f =+ , f(x)=o(x)

Démonstration

III.c).1) on a x^1/2=V₁(x)f(x) xR^+*, donc x^-1/2f(x)/x et finalement :

donc f admet une tangente verticale en x=0.
Si x=0, pour n1 U_n(x)=U_n-1(x)/2=2^-n, et V_n(x)=0 donc f(0)=0

---

III.c).2) D'après II.b) et II.c),
xR^+*, f(x)=M(1,x)=xM(1/x,1)=xM(1,1/x)=xf(1/x)

Quand x -> + lim f(1/x)=f(0)=0 car f est continue en 0
donc f(x)/x->0 et en +, f(x)=o(x)

De plus xR^+*, f(x)x^1/2, donc en +, lim f=+

---

III.d) Théorème 5

f est de classe C sur ]0,+[

Ce résultat très fort (presque trop puisque nous n'aurons besoin que du caractère C¹ !) n'est pas simple à démontrer. Il va même nous entraîner dans la théorie des intégrales elliptiques !
Ainsi, nous allons successivement :
III.d).1) Exprimer M(a,b) par une intégrale elliptique I(a,b)
III.d).2) Appliquer ce résultat à la fonction f
III.d).3) Utiliser le caractère C de I(1,x) pour en déduire celui de f !

Démonstration

III.d).1) On s'intéresse tout d'abord à l'intégrale suivante,
Soient a,b>0, on pose :

III.d).1).i) Convergence

Soit et m(0)=1/(ab), or m étant bien sûr continue sur R⁺, m est intégrable sur R⁺ et donc I(a,b) est bien définie...

---

III.d).1).ii) Changement de variable

Posons
c'est une bijection croissante donc effectuons un petit changement de variables... Posons t=b.tan(y), on obtient :

---

III.d).1).iii) fonction g

On définit la fonction g par g(x)=I(1,x)

Montrons qu'elle est de classe C sur ]0,+[

Soit h(x,y)= avec (x,y)]0,+[*[0,/2]

Montrons par récurrence sur nN (toujours !) que existe et est continue sur ]0,+[*[0,/2]
Pour cela, montrons en même temps, toujours par récurrence, qu'avec les hypothèses sur les paramètres :

(x,y)= où x -> P_n(x,y)R_n[x]

• n=0, c'est la définition même de h !
  h est clairement continue sur ]0,+[*[0,/2] et admet une dérivée partielle selon x
• n=1 :
  C'est bien la forme annoncée pour n=1 et c'est parfaitement continu sur ]0,+[*[0,/2]
• Supposons maintenant le résultat pour un certain nN
  
  ce qui est bien le résultat attendu avec P_n+1 de la forme voulue... P_n+1 est un polynôme en x et un polynôme trigonométrique en y et est donc à ce titre continu sur ]0,+[*[0,/2] et dérivable selon x. De même pour le dénominateur, donc l'hypothèse est vérifiée au rang n+1, ce qui achève la récurrence !

h est donc de classe C sur ]0,+[*[0,/2]

Puisque l'on se place sur le segment [0,/2] pour y, la fonction g définie par :

g(x)=h(x,y)dy

est elle même de classe C sur R^+* et l'on a :

g⁽ⁿ⁾(x)=(x,y)dy

x -> I(1,x) est donc une fonction de classe C sur R^+*

Reste à exprimer M(a,b) en fonction de I(a,b)

C'est là bien sûr le principal résultat de cette étude et il fut obtenu par Gauss (il n'a pas été plus loin !).

---

III.d).1).iv) Montrons tout d'abord que :

=I (a,b)

Pour cela, posons j(t)= définie sur R^+* et qui est clairement une bijection de R^+* sur R ( j'(t)=>0 ) donc, dans I(1,t) définie au 1), on pose s= et on obtient :

et d'autre part, ds=dt, donc on obtient finalement :

L'avant dernière égalité étant obtenue grâce à la parité du terme sous l'intégrale

---

III.d).1).v) Alors, on avance bien, montrons maintenant que
On a clairement I(ßa,ßb)=I(a,b)/ß donc :



or a_n=M(a,b) et on a a_n/b_n=1.
De plus, g est continue sur R^+* d'après iii) donc :

ce qui nous permet de conclure :

---

III.d).2) en appliquant ce résultat à la fonction f, on obtient

---

III.d).3) Et la démonstration du théorème 5 est finie, g étant C sur R^+*, f l'est également sur le même intervalle

Petite note : f est continue en 0 mais n'est pas dérivable en 0 d'après le lemme 4...

---

III.e) Comportement asymptotique de f

Nous allons chercher des équivalents de f aux bornes de R⁺ au moyen d'équivalents de g

Lemme 6


Démonstration

III.e).1) Une nouvelle expression de g !

Posons à tout hasard (!) s=x/t :

---

III.e).2) Trouvons maintenant un équivalent de g au voisinage de 0

t[0,x^1/2], on a 11+t²1+x, donc




donc d'après III.d).2) on a :

la deuxième équivalence étant obtenue trivialement grâce à III.c).2) (f(x)=x.f(1/x))

---

IV Expression de Pi en fonction de f et f'

Nous allons montrer que =

Pour cela, on restreint U_n et V_n à ]0,1[ et on introduit W_n et k_n, fonction définie sur ]0,1[ par :

W_n= et

Ces fonctions sont évidemment bien définies et positives car d'après III a)2) 0<V_n(x)<U_n(x) sur ]0,1[

---

IV.a) Convergence de (k_n)_n

IV.a).1) Propriété

2M(Un+1,Wn+1)=M(Un,Wn)

Démonstration



Posons a=U_n+V_n=a₀, b=U_n-V_n=b₀ comme au I, on a

---

IV.a).2) Convergence



Démonstration

---

Démonstration



donc d'après l'étude asymptotique du III e), on obtient :

d'après la propriété précédente, ce qui permet en rapprochant les deux égalités de conclure à :

fort !

---

IV.b) Convergence de (k'_n)_n

Intéressons nous désormais à la suite de fonctions dérivée (k'_n)_n. En effet, f'apparaît dans l'expression finale recherchée, il y a ainsi de grandes chances pour que l'on parle de suites dérivées à un moment... Cela se précise donc :

IV.b).1) Existence et positivité

nN, Un, Vn, Wn, kn sont continûment dérivables De plus, x]0,1[, nN*, U'n>0, V'n>0

De même que pour la continuité de U_n et V_n, on fait une récurrence sur n entier pour prouver cela. Abrégeons donc !
U₁ et V₁ vérifient évidemment la propriété et si l'on suppose la propriété vraie pour un certain n, un petit calcul d'après la définition de U_n et V_n donne
ce qui assure l'existence, la continuité et la positivité au rang n+1... Hop, c'est fini, inutile de s'attarder sur de telles récurrences !

W_n et k_n étant des composées de fonctions continûment dérivables, elles le sont aussi pour tout n...

---

IV.b).2) Expression de (k'_n)

x]0,1[, nN,

Démonstration :

d'après IV a)1) donc



or V_n²=U_n²-W_n² et en dérivant, 2V_nV_n'=2U_nU_n'-2W_nW_n' donc :



et on obtient finalement :

---

IV.b).3) Convergence

(k'n) converge uniformément sur tout compact de ]0,1[ vers : x->

Démonstration

Plaçons-nous sur [a,b] compact de ]0,1[, 0<a<b<1
nN, x[a,b], on a :


en utilisant III.a).2)...

Cette majoration uniforme entraîne la convergence uniforme de (k'_n)_n vers
x -> sur tout compact de ]0,1[

---

IV.c) Expression de Pi

Nous y sommes enfin !

IV.c).1) Dérivée

x -> est la dérivée de x ->

Démonstration

• nN, k_n est de classe C¹ sur ]0,1[ d'après IV b)1)
• La suite de fonctions (k_n) converge simplement sur ]0,1[ vers la fonction
  x-> d'après IV a)2)
• La suite de fonctions (k'_n) converge uniformément sur tout compact de ]0,1[ vers x ->

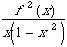
Donc en application du théorème de dérivation des suites de fonctions (Prépa !),
x-> est la dérivée sur ]0,1[ de x ->

---

IV.c).2) Equation différentielle

f vérifie l'équation différentielle : x]0,1[,

Démonstration

Facile ! Il suffit de dériver x -> et d'utiliser le résultat précédent a).
Je ne le fais pas, ce n'est que du calcul !

---

IV.c).3) Expression de Pi

La quête du Saint-Graal mathématique irait-elle vers son terme ? En tout ca, on touche ici au résultat le plus important de la démo !

=

Référence de l'Encyclopédie des Suites Entières sur M(1,sqrt(2)) : A003054

Démo

Là, encore, très facile, il suffit de faire x= dans l'équation différentielle. Pareil, ce n'est que du calcul, je ne vais pas encore alourdir le chargement de cette page avec des expressions inutiles.

C'est tout de même un résultat formidable !
Et qui va être la base de la construction de plusieurs algorithmes très performants à convergence quadratique

---

V Applications


Passons aux choses sérieuses !
Plusieurs exploitations de cette formule sont possibles :

V.a) Utilisation directe des suites dérivées

La première à laquelle on pense tout de suite est d'utiliser les suites de fonctions dérivées (U'_n) et (V'_n) convergeant vers f' (la démonstration de cette convergence est donnée au V.b) ). On obtient en remplaçant f et f' par U_n et V_n de différentes façons l'algorithme suivant :

Même s'il paraît plus compliqué que les algorithmes de Borwein ou Brent/Salamin, je me suis étonné de ne le trouver absolument nulle part ! Mais dans mon souci d'exhaustivité, je ne pouvais manquer de le signaler.

---

V.b) Algorithme de J. and P. BORWEIN (1987)

Cet algorithme est paru dans Pi and the AGM (j'en ai un exemplaire, c'est formidable !!). Je vais en donner la démonstration détaillée et en évaluer la performance... Il est donné sous la forme :

Démonstration

On se placera durant toute la démo sur un compact K de ]0,1[
Avec les notations des parties précédentes, posons pour n1 :

V.b).1) Convergence

Montrons que :

yn1, zn1, nN* (yn) et (zn) convergent uniformément vers 1 sur K

Démonstration

* D'après III.a).2). et la définition de y_n et z_n, U_nV_n, donc y_n1
* nN, x]0,1[

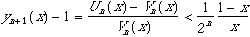
d'après III.a).2). et V_n(x)>V₀(x)=x.
Sur K, on a de plus x->1/x-1 est bornée (continue sur un compact) par un certain MR^+*, donc

xK, y_n(x)-1<M.2^-n

De ce fait, (y_n) converge uniformément vers 1 sur K

* Montrons par récurrence sur nN* que z_n1

n=1 : z₁=x^-1/2>1 sur ]0,1[
Supposons le résultat pour un certain nN*

ce qui montre en passant les relations de récurrence pour (y_n) et (z_n) !
donc

car z_n1 par hypothèse de récurrence et y_n1 d'après précédemment, en conséquence ceci achève la récurrence...

Pour n1, z_n+1-y_n+1 est du signe de :
2(1+y_nz_n)-(1+z_n)(1+y_n)=1+y_nz_n-z_n-y_n=(z_n-1)(y_n-1)0
donc

z_n+1y_n+1

De même, z_n+1-y_n^1/2 est du signe de :
1+y_nz_n-y_n(1+z_n)=1-y_n0
or y_n1 donc y_n^1/2y_n et finalement :

y_n+1z_n+1y_n^1/2y_n

donc 0<y_n+1-1<z_n+1-1<y_n-1 et :

Sup_K(z_n+1(x)-1)Sup_K(y_n(x)-1)

La convergence uniforme de (y_n) vers 1 sur K assure, par là même, la convergence uniforme de (z_n) vers 1 sur K...

---

V.b).2) Montrons maintenant que (U'_n) et (V'_n) convergent uniformément sur K. C'est certainement la démonstration la plus pénible à obtenir, mais elle marche et c'est bien le principal !!

Soit donc x]0,1[, nN*,
z_n1, donc U'_nV'_n et comme U'_n+1=(U'_n+V'_n)/2 on a U'_n+1U'_n
(U'_n) est donc croissante
V'_n+1(x)-V'_n(x)= donc le signe de V'_n+1(x)-V'_n(x) est celui de :
.

En divisant par U'_n(x)V'_n(x)>0 on obtient :


or, d'après a), y_n^1/2-1y_n-1z_n-1, et (z_n) converge uniformément vers 1 sur K donc à partir d'un certain rang n₀, pour nn₀,
xK, 0<z_n(x)-1<1/2, d'où :

car z_n(x)2

ainsi pour nn₀ et xK, V'_n+1(x)V'_n(x) et finalement :

U'_n(x)U'_n+1(x)V'_n+1(x)V'_n(x)

Ceci étant, soit ß>0
(z_n) converge uniformément vers 1 sur K, donc il existe n₁N tel que :

nn₁ => 0sup_K(z_n(x)-1)<ß*V_no(x)^-1

or
avec nMax(n₀,n₁) et puisque (V'_n) est décroissante d'après ci-dessus (eh oui !), on a pour nMax(n₀,n₁) V'_n(x)V'_no(x), donc :

0V'_n(x)-U'_n(x)<ßV'_no(x)V'_no(x)^-1=ß

x]0,1[, (U'_n(x) et (V'_n(x)) sont de ce fait des suites adjacentes et convergent vers une limite commune que l'on notera µ(x).
On a donc :

x]0,1[, 0U'_n(x)U'_n+1(x)µ(x)V'_n+1(x)V'_n(x)

Pour nMax(n₀,n₁) on a donc :

x]0,1[, 0µ(x)-U'_n(x)V'_n(x)-µ(x)ß

Donc les suites (U'_n) et (V'_n) convergent uniformément sur K vers µ(x)

V.b).3) Construisons maintenant la suite (f_n) (enfin !)

(U_n) converge uniformément (donc a fortiori simplement) sur K vers f et (U'_n) converge uniformément sur K donc sa limite est f' sur ]0,1[

Posons

On a :

puis

ce qui achève la démonstration. Ah ! quel beau résultat !

Performance

Toute la longueur des démonstrations du XXe siècle trouve sa récompense au chapître des performances (encore heureux !)
Cet algorithme est en effet à convergence quadratique. C'est-à-dire que le nombre de décimales exactes double à chaque itération, mais cela ne se voit pas au premier abord !

Montrons donc que :

Démonstration

Soit nN.


Pour x=2^-1/2, un petit calcul numérique donne :

D'autre part,


Or, on a , les termes se compensant deux à deux. On fait alors tendre k vers +, et on obtient :

---

V.c) Algorithme de Brent/Salamin (1976)

L'algorithme originel est celui-ci, on ne pouvait donc passer outre sa démonstration, que je n'ai d'ailleurs étonnament trouvée nulle part, mais il n'est pas trop dur de la refaire, grâce à tout le boulot réalisé précédemment !

Cet algorithme est donné sous la forme :



Démonstration

Elle est très rapide ! Reprenons exactement les mêmes notations que pour la démo précédente...

V.c).1) Rappelons nous : k_n=
or W_n= donc


or d'après IV.b).2), sur ]0,1[ en conséquence

en x=2^-1/2

V.c).2) Posons d'autre part


calculons (encore !) :
(tiens !)



Par récurrence immédiate, on a donc :

en simplifiant les notations.

Donc, on obtient finalement:



ce qui achève toute la partie démo et me donne droit à un repos bien mérité (Ouf ! cette page était bien longue...)

---

Essais

Les suites présentées ont des performances similaires. Par exemple, concernant la seconde (Borwein), pour obtenir 10 000 000 de décimales de Pi, il suffit d'avoir n19 !!!

Les essais sont assez extraordinaires :

n=	1	2	3	4	5	6	7	8	9	10
d=	2	8	18	40	83	170	344	693	1392	2789

d est le nombre de décimales exactes de Pi
La convergence quadratique est parfaitement respectée, c'est à dire que le nombre de décimales exactes double à chaque itération.

De plus, le temps de calcul de n décimales, qui nécessite pour les méthodes classiques un temps proportionnel à n², se trouve réduit à environ n.Log(n) avec les algorithmes de Brent/Salamin et Borwein... Une petite révolution !