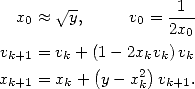|
|
|
|
|

Algorithme de Newton
1 La racine de tous les maux
Imaginez que l’on vous demande les premières décimales de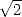 . Silence pendant quelques secondes...
mmmmh... bon, c’est plus que 1, moins que 2 car
. Silence pendant quelques secondes...
mmmmh... bon, c’est plus que 1, moins que 2 car 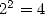 ... C’est moins que 1.5 car
... C’est moins que 1.5 car 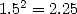 etc... Rien
de très simple... Alors comment les mathématiciens du 17e siècle pouvaient-ils approcher numériquement les
solutions d’un polynôme du 4e degré ?
etc... Rien
de très simple... Alors comment les mathématiciens du 17e siècle pouvaient-ils approcher numériquement les
solutions d’un polynôme du 4e degré ?
Toujours prolifique, Newton proposa vers 1669 (!) un processus itératif convergeant de manière
quadratique vers de telles solutions, c’est-à-dire que le nombre de décimales exactes de la solution proposéee
double à chaque itération. Du coup, cela ramèna la complexite algorithmique de la division et de l’extraction
de racines carrées à celle de la multiplication. Une aubaine pour les calculateurs modernes, confrontés dans
leur quête du record de décimales de 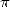 à de douloureuses extractions de racines carrées dans les algorithmes
de Salamin ou des frères Borwein. Cet algorithme a bien d’autres propriétés que je vous propose de découvrir
ci-dessous.
à de douloureuses extractions de racines carrées dans les algorithmes
de Salamin ou des frères Borwein. Cet algorithme a bien d’autres propriétés que je vous propose de découvrir
ci-dessous.
2 Enoncé de l’algorithme de Newton
L’algorithme de Newton, vieux de plus de trois siècles, est à l’origine utilisé pour approcher numériquement
une racine  de l’équation
de l’équation 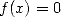 . Il permet en fait de montrer l’équivalence de la multiplication, la
division et l’extraction de racines carrées d’un point de vue complexité.
. Il permet en fait de montrer l’équivalence de la multiplication, la
division et l’extraction de racines carrées d’un point de vue complexité.
Newton avait proposé dès 1669 un processus itératif pour trouver les racines d’équations polynomiales et Raphson le mit sous forme plus algorithmique en 1690. Simpson, Mourraille, Cauchy et Kantorovich ajoutèrent des raffinements et proposèrent des généralisations pour arriver à l’énoncé moderne suivant
Theorem 2.1 Soit 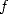 analytique dans un voisinage complexe de
analytique dans un voisinage complexe de  . Supposons que
. Supposons que 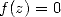 et
et
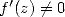 . Alors l’itération
. Alors l’itération
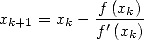 | (1) |
converge uniformément et quadratiquement vers  pour une valeur initiale
pour une valeur initiale 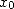 prise dans un voisinage de
prise dans un voisinage de
 .
.
Cet algorithme s’accompagne d’une propriété étonnante d’auto-compensation des erreurs : si 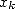 est
perturbé et ne compte plus que
est
perturbé et ne compte plus que 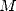 décimales justes par rapport à
décimales justes par rapport à  alors le terme
alors le terme 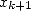 contiendra tout
de même
contiendra tout
de même 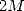 décimales exactes s’il a été calculé avec suffisamment de décimales, autrement dit la
convergence quadratique sera préservée.
décimales exactes s’il a été calculé avec suffisamment de décimales, autrement dit la
convergence quadratique sera préservée.
Une conséquence directe est que pour calculer  avec
avec 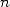 décimales, il suffit d’initier l’algorithme avec
quelques décimales au début et doubler la précision prise en compte à chaque itération jusqu’à atteindre une
précision supérieure à
décimales, il suffit d’initier l’algorithme avec
quelques décimales au début et doubler la précision prise en compte à chaque itération jusqu’à atteindre une
précision supérieure à 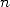 . Ceci simplifie considérablement la complexité de l’opération et permet de montrer
que la multiplication, la division et l’extraction de racines carrées sont équivalentes en complexité
:
. Ceci simplifie considérablement la complexité de l’opération et permet de montrer
que la multiplication, la division et l’extraction de racines carrées sont équivalentes en complexité
:
3 Applications
3.1 Inverse d’un nombre
Prenons l’exemple d’un nombre 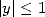 dont on souhaite calculer l’inverse avec
dont on souhaite calculer l’inverse avec 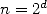 décimales exactes.
En utilisant la fonction
décimales exactes.
En utilisant la fonction 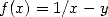 , l’itération associée est
, l’itération associée est
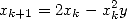 | (2) |
qui utilise uniquement des multiplications et additions. L’expression
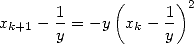 | (3) |
illustre la convergence quadratique de l’algorithme. Initions maintenant l’itération avec une décimale exacte, soit
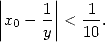 | (4) |
Grâce à la propriété d’auto-correction de la méthode de Newton, à l’itération 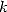 , on n’utilise que
, on n’utilise que 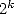 décimales pour les calculs. Et d’après 2, pour obtenir
décimales pour les calculs. Et d’après 2, pour obtenir 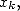 on a uniquement besoin de
on a uniquement besoin de  multiplications
(
multiplications
(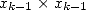 et
et 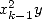 ) et
) et  additions (
additions (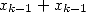 et
et 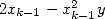 ). En raison de la
convergence quadratique, il suffira d’environ
). En raison de la
convergence quadratique, il suffira d’environ 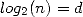 itérations de 2 pour parvenir à
itérations de 2 pour parvenir à 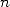 décimales exactes de
décimales exactes de 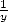 . Si on note
. Si on note 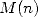 la complexité d’une méthode de multiplication pour
la complexité d’une méthode de multiplication pour 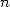 décimales, sachant que la complexité d’une addition sera
décimales, sachant que la complexité d’une addition sera 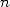 , on obtient alors une complexité finale
de
, on obtient alors une complexité finale
de
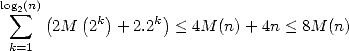 | (5) |
Il est en effet raisonnable d’envisager 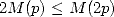 autrement dit que la complexité de
autrement dit que la complexité de  multiplications
de nombres à
multiplications
de nombres à 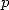 décimales requiert un peu moins de complexité que la multiplication de deux nombres à
décimales requiert un peu moins de complexité que la multiplication de deux nombres à 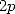 décimales. Ceci induit
décimales. Ceci induit 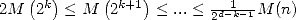 dans 5. L’inversion n’est donc guère plus
compliquée que la multiplication (c’est un
dans 5. L’inversion n’est donc guère plus
compliquée que la multiplication (c’est un 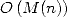 ) et comme
) et comme 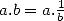 , la division est elle aussi un
, la division est elle aussi un
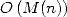 .
.
3.2 Extraction de racines carrées
Les choses se passent aussi bien. On peut utiliser la fonction 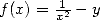 qui conduit à l’approximation de
qui conduit à l’approximation de
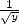 puis on fait
puis on fait 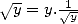 . L’itération associée est
. L’itération associée est
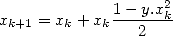 | (6) |
ce qui conduit en pratique à une complexité finale d’environ 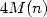 .
.
Une alternative plus naturelle est d’utiliser directement la fonction 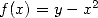 , mais cela conduit à
une itération comprenant une division disqualifiante
, mais cela conduit à
une itération comprenant une division disqualifiante
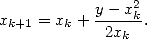 | (7) |
Cependant, Schönhage, qui ne manquait pas d’idées (voir page FFT), a proposé en 1971 de remplacer 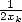 par une approximation tirée d’une itération couplée et a obtenu
par une approximation tirée d’une itération couplée et a obtenu
Ce processus, où 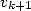 estime
estime 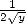 , est appelé ”itération couplée de Newton” ([5], p257) et requiert en
pratique une complexité d’environ
, est appelé ”itération couplée de Newton” ([5], p257) et requiert en
pratique une complexité d’environ 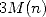 .
.
On trouvera de nombreux raffinements de la méthode de Newton dans [1, 4] et l’équivalence de la complexité de la multiplication, la division et l’extraction de racines est abordée dans [2, 3].
References
[1] J. Arndt, C. Haenel, ”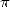 Unleashed”, Springer-Verlag, Berlin Heidelberg New York, 2001.
Unleashed”, Springer-Verlag, Berlin Heidelberg New York, 2001.
[2] R. Brent, “Fast multiple-precision evaluation of elementary fonctions”, Journal of the Association of Computing Machinery, 1976, pp.242-251.
[3] S. A. Cook, S. O. Aanderaa, “On the minimum computation of functions”, Trans. AMS, 1969, vol. 142, pp291-314.
[4] M. D. Householder, “The Numerical Treatment of a Single Nonlinear Equation”, 1970, MacGraw-Hill, New-York.
[5] A. Schönhage, V. Strassen, “Schennelle Multiplikation grosser Zahlen”, Computing, 1971, vol. 7, pp. 281-292.
Retour à la page d'accueil