François Viete
(1540 - 1603)

soit :

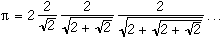
Tranches de vie

François Viete, né à Fontenay-le-comte en 1540 est tout d'abord diplomé de droit en 1560. Mais parallèlement à sa carrière juridique, il s'intéresse aux sciences. Il écrit ainsi un traité d'astronomie ( Principes de cosmographie ); mais banni en 1584 pour 5 ans, il commence, ayant du "temps libre", à s'intéresser aux mathématiques !
C'est sa période la plus féconde. Travaillant sur l'algèbre et principalement sur les polynômes, il simplifie quelque peu les notations et trouve une méthode de résolution des équtions du troisième degré.
Il s'intéresse également à l'expression de cos(nx) et sin(nx) en fonction de cos(x) et sin(x), ce qui donne ce que nous appelons maintenant les polynômes de Tchebychev.

Autour de

Ses recherches en trigonométrie l'amènent à calculer neuf décimales de Pi (et pas sept comme c'est écrit dans l'Encyclopédie Universalis !). Mais surtout, Viete énonce le premier produit infini connu valant Pi ! Malheureusement, il ne se soucie pas de la convergence effective de son produit. Celle-ci ne sera prouvée qu'au XIXe siècle en 1892 par Rudio. Viète utilise non pas les périmètres comme Archimède mais les aires des polygones.

Démonstration

Les deux algorithmes du haut de la page sont équivalents, ce qui est immédiat par récurrence.
Ensuite, il y a deux méthodes. Celle du paresseux qui consiste à remarquer que les deux algorithmes sont équivalents à la suite d'Archimède où aura été multiplié par son conjugué (+ à la place du premier moins) puis où l'on aura simplifié.
Et puis il y a la construction géométrique, lourde mais intéressante car proche de l'inspiration originale du mathématicien, et que je présente ici :

Viete s'intéresse à l'aire des polygones réguliers inscrits dans un cercle de rayon unité dont on doublerait à chaque fois le nombre de côtés (tiens comme c'est étonnant !)

Cette aire finirait par tendre vers celle du cercle soit .
Pour ce faire, il divise un polygone à n côtés en n triangles dont il calcule l'aire.

On a : OH=Rcos() et IJ=2JH=2Rsin()
Bien...
Puis on note A_n l'aire du polygone à n côtés :

Si on double le nombre de côtés du polygone, on divise par 2 et cette nouvelle aire vaut :


Posons maintenant :

or l'aire A d'un cercle est donnée par A=R²= donc =A_n /P.
Mais si l'on fait tendre k vers l'infini, P s'écrit comme un produit de cos
(car dans ce cas, A_kn -> A), donc on peut écrire :

Or, on sait que :


A_n étant l'aire du premier polygone avec n=4 (carré =p/4), on a A_n=n.sin()cos()=2 et U₀=2^-1/2
Donc finalement on obtient :

Notons que si l'on part d'un autre polygone, on arrive à une autre expression (comme le diraient les profs de facs dans leurs polys, je laisse cela à l'attention du lecteur !)

Convergence du produit :

Ce résultat est assez simple mais indispensable :



(Evidemment, cela n'aurait pas de sens normalement de noter la somme si elle n'existait pas, mais l'étude des probabilités m'a montré qu'il n'y avait pas de problèmes à écrire cela notamment dans cette discipline puisque la somme peut être égale à l'infini, tout simplement... et il n'y a pas de gêne à l'écrire si c'est compréhensible)
le produit converge également, donc la suite a bien un sens.

Essais

Bah, si le produit infini de Viète descend de celui d'Archimède, normalement nous allons être confronté à une convergence linéaire :

n=5	3,141277 (3)
n=10	3,1415923 (6)
n=50	30 décimales justes
n=100	60 décimales justes

Pas de problèmes ! Une belle convergence en 3n/5 comme pour Archimède.

Accélération de la convergence

Et comme pour ce bon vieux Archimède, il y a une très efficace accélération de la convergence par le Delta2 d'Aitken :

n=5	3,14159280 (6)
n=10	3,14159265358993 (12)
n=50	60 décimales justes

Eh bien, rien de moins qu'un doublement de la rapidité de convergence !!