Al Kashi
(? - 1429)

Tranches de vie

Son véritable nom était "ghiyat al-dîn djamashîd b.mahs'ûd b.mahmûd al Kashi" (rien que ça !) mais il est plus connu sous le nom écourté d'Al Kashi, du lieu de naissance Kachan entre Ispahan et Téhéran. Mathématicien célèbre à son époque, il est mort à Samarkand en 1429. Son oeuvre majeure, le traité du cercle (Risala a-muhitiyya), a été écrite en 1424 en arabe.

Autour de

Dans celui-ci, bien qu 'il n'y ait rien de véritablement neuf depuis Archimède, sa virtuosité calculatoire l'incite à se lancer un défi : calculer une bonne approximation de 2 (rapport entre la circonférence du cercle et son rayon). "Bonne" signifie pour lui que pour un cercle 600 000 fois plus grand que l'équateur terrestre, l'incertitude doit être inférieure à "un crin de cheval". Ce qui représente 16 décimales exactes de ou, dans la base 60 qu 'utilise Al Kashi, 10 places sexagésimales. Celui-ci exhibe en effet dans son ouvrage 6 ⁰16 ^I59 ^II28 ^III1 ^IV34 ^V51 ^VI46 ^VII14 ^VIII50 ^IX !

Démonstration

La méthode est, comme toujours à cette époque, celle d'Archimède, puisque Al Kashi part d'un hexagone et donc d'un côté de longueur 2sin(/6)=1. On pose

C_n=

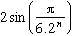
Par équivalence de x et sin(x) si x tend vers 0, 3.2ⁿ.C_n tend vers lorsque n tend vers l'infini.
La relation de récurrence se trouve alors en utilisant la formule de trigonométrie cos²(x)+sin²(x)=1, et cos(x)=1-2sin²(x/2). On a immédiatement . Ce qui donne en remplaçant x par /(6.2ⁿ) la formule demandée en C_n.

Essais

La formule étant presque la même que celle d'Archimède à un facteur 2 près, les essais et performances sont parfaitement similaires ! Il en est de même pour l'accélération de la convergence par le Delta2 d'Aitken.