|
|
|
|
|

Atteindre le 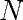 -ième digit d’un nombre
-ième digit d’un nombre 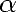 sans connaitre les
précédents grâce aux formule BBP
sans connaitre les
précédents grâce aux formule BBP
1 La formule BBP
Petit rappel: le 19 septembre 1995 à 0h29 (!), après des mois de recherches à tâtons, Simon Plouffe, David Bailey et Peter Borwein de Vancouver découvrent la formule apparemment simple et anodine
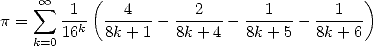 | (1) |
appelée depuis formule BBP (voir page Plouffe). Nos trois mathématiciens canadiens remarquent que cette
expression est très proche d’une décomposition en base 16 de 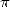 . Dans l’article [1] de 1996 devenu célèbre, ils
montrent que l’on peut se servir de 1 pour atteindre le
. Dans l’article [1] de 1996 devenu célèbre, ils
montrent que l’on peut se servir de 1 pour atteindre le  -ième digit de
-ième digit de 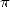 en base
en base 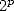 (a fortiori en base 16)
sans avoir calculé les précédents, ceci en temps presque linéaire
(a fortiori en base 16)
sans avoir calculé les précédents, ceci en temps presque linéaire 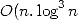 ) et en espace
) et en espace 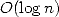 !!
L’espace requis étant minime, ils appliquent immédiatement ce résultat en calculant le
!!
L’espace requis étant minime, ils appliquent immédiatement ce résultat en calculant le 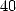 milliardième digit
de
milliardième digit
de 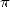 en base 2.
en base 2.
Arrêtons-nous maintenant sur le principe de ce calcul du 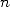 -ième digit de
-ième digit de 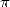 en considérant le cas général
d’un nombre
en considérant le cas général
d’un nombre  et d’une formule BBP associée:
et d’une formule BBP associée:
2 Atteindre le 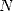 -ième digit d’un nombre
-ième digit d’un nombre  sans connaitre les précédents
sans connaitre les précédents
Nous suivons ici à quelques adaptations près l’exposé remarquablement clair de Xavier Gourdon et Pascal
Sebah sur le sujet [2] qui simplifiait déjà l’article original [1]. X. Gourdon est un grand connaisseur des
algorithmes de calcul puisqu’il détient depuis plusieurs années le record de vitesse du calcul des
décimales de 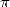 avec le programme PiFast (plus rapide même que le programme de l’équipe de
Kanada).
avec le programme PiFast (plus rapide même que le programme de l’équipe de
Kanada).
Pour simplifier le propos, on se restreint à la base  , et le
, et le 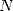 -ième bit de
-ième bit de  désigne le
désigne le 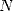 -ième bit de
la partie fractionnaire de
-ième bit de
la partie fractionnaire de  , c’est-à-dire après la virgule. La partie fractionnaire d’un nombre
, c’est-à-dire après la virgule. La partie fractionnaire d’un nombre  sera notée
sera notée
![{x}= x- [x]](../mathematiciens/nieme_digit/nieme_digit25x.gif) .
.
2.1 Décalage
La première idée repose sur le théorème suivant
Theorem 2.1 Le 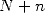 -ième bit de
-ième bit de  s’obtient en calculant le
s’obtient en calculant le 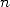 -ième bit de
-ième bit de 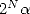 i.e. le
i.e. le
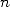 -ième bit de
-ième bit de 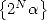 .
.
Proof. La décomposition en base  de
de  s’écrit
s’écrit
![a = [a]+ {a}= sum ak+ sum ak, (a (- {0,1})
2k 2k k
k<0 k>0](../mathematiciens/nieme_digit/nieme_digit34x.gif) | (2) |
d’où  . Le
. Le  -ième bit de
-ième bit de  est donc
est donc 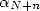 qui est bien le
qui est bien le
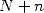 -ième bit de
-ième bit de  .
__
.
__
Example 2.2 Cherchons le 13ème bit de 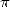 . Comme on a
. Comme on a 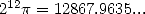 , en particulier,
, en particulier,
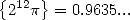 . Il reste donc à calculer le
. Il reste donc à calculer le 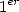 bit de
bit de 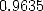 . En passant en binaire, on
a
. En passant en binaire, on
a
![-1 1- -1 1- 0- -1 1-
0.9635...= 21 + 22 + 23 + 24 + 25 + 26 + 27 + ...= [0.1111011...]base 2](../mathematiciens/nieme_digit/nieme_digit46x.gif) | (3) |
donc le 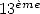 bit de
bit de 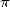 est
est 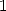 , et le
, et le 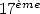 bit est
bit est  .
.
Chercher le 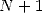 -ième bit de
-ième bit de 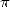 correspond donc à trouver le premier bit de
correspond donc à trouver le premier bit de 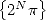 . D’après la
formule BBP 1, cela correspond au premier bit de la série
. D’après la
formule BBP 1, cela correspond au premier bit de la série
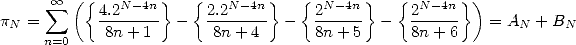 | (4) |
où 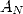 et
et 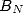 sont les sommes
sont les sommes
 | (5) |
Compte tenu de la décroissance rapide de 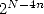 pour
pour 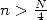 , il suffit d’évaluer seulement les premiers
termes de
, il suffit d’évaluer seulement les premiers
termes de 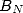 (en virgule flottante !), plus exactement suffisamment pour que le reste de la somme soit
inférieur à la précision requise (ici
(en virgule flottante !), plus exactement suffisamment pour que le reste de la somme soit
inférieur à la précision requise (ici 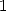 bit après la virgule).
bit après la virgule).
Concernant 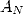 , on peut mettre son terme général sous la forme
, on peut mettre son terme général sous la forme
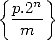 | (6) |
avec 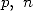 et
et 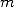 dans
dans 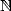 . En écrivant
. En écrivant 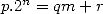 la division euclidienne de
la division euclidienne de 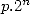 par
par 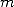 , on voit que
comme
, on voit que
comme 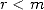 ,
, 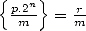 . Ceci s’écrit encore
. Ceci s’écrit encore
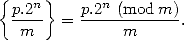 | (7) |
2.2 Exponentiation
Imaginons ainsi que l’on veuille calculer le 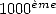 bit de
bit de 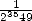 . Grâce aux principes précédents, cela
revient à calculer le
. Grâce aux principes précédents, cela
revient à calculer le 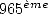 bit de
bit de 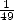 et donc le
et donc le 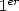 bit de
bit de 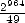 . En vertu de 7, il faut alors trouver
. En vertu de 7, il faut alors trouver  tel que
tel que 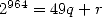 donc évaluer
donc évaluer 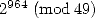 .
.
Le calcul de 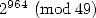 s’effectue au moyen de la méthode appelée exponentiation binaire (“binary
powering” ou “binary exponentiation”), dont l’idée semble avoir été utilisée dès 200 avant J.C [3], et
même envisagée par les Egyptiens pour effectuer la multiplication ! Cela revient simplement
à utiliser l’arithmétique modulo
s’effectue au moyen de la méthode appelée exponentiation binaire (“binary
powering” ou “binary exponentiation”), dont l’idée semble avoir été utilisée dès 200 avant J.C [3], et
même envisagée par les Egyptiens pour effectuer la multiplication ! Cela revient simplement
à utiliser l’arithmétique modulo 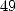 , autrement dit à se placer dans
, autrement dit à se placer dans 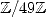 , en trois étapes
:
, en trois étapes
:
- On décompose
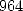 en puissances de
en puissances de  :
: 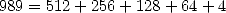
- On calcule de proche en proche chaque puissance de
 jusqu’à
jusqu’à 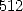 :
: 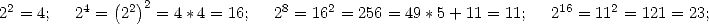
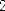
- On utilise les étapes 1 et 2 :
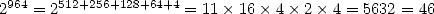 .
.
Pour obtenir plus généralement 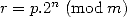 , on initialise
, on initialise  à 1 et on prend
à 1 et on prend 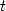 la plus grande
puissance de
la plus grande
puissance de  inférieure à
inférieure à 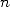 . Puis on applique l’algorithme suivant équivalent à notre exemple
:
. Puis on applique l’algorithme suivant équivalent à notre exemple
:
Enfin on termine par 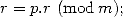 pour prendre en compte
pour prendre en compte 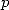 . En raison de la décomposition de
. En raison de la décomposition de 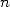 en
puissance de
en
puissance de  , on utilise
, on utilise  opérations pour ce calcul, ce qui est très faible
!
opérations pour ce calcul, ce qui est très faible
!
2.3 Etapes finales
Il reste à obtenir 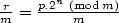 et à sommer le tout sur
et à sommer le tout sur 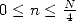 pour obtenir
pour obtenir 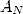 dans 5.
Il faut ici remarquer que si le calcul de chaque terme de
dans 5.
Il faut ici remarquer que si le calcul de chaque terme de 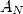 est effectué en virgule flottante
et que, disons, le dernier bit est erroné, alors au pire la propagation des retenues sur toute la
somme produira une erreur sur
est effectué en virgule flottante
et que, disons, le dernier bit est erroné, alors au pire la propagation des retenues sur toute la
somme produira une erreur sur 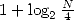 bits. Pour des valeurs de
bits. Pour des valeurs de 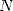 non extravagantes, on
pourra donc mener les calculs de
non extravagantes, on
pourra donc mener les calculs de 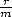 en toute sérénité avec une précision arithmétique de
en toute sérénité avec une précision arithmétique de 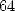 bits
seulement.
bits
seulement.
Pour cette raison et en remarquant que pour 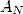 , on somme
, on somme 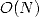 termes nécessitant chacun
termes nécessitant chacun
 opérations grâce à l’exponentiation, l’algorithme requiert
opérations grâce à l’exponentiation, l’algorithme requiert 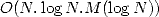 opérations et
opérations et
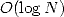 en espace, où
en espace, où 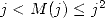 est la complexité de la multiplication de deux entiers de taille
est la complexité de la multiplication de deux entiers de taille 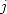 bits.
bits.
References
[1] D.H. Bailey, P.B. Borwein, S. Plouffe, “On the Rapid Computation of Various Polylogarithmic Constants”, Mathematics of Computation, 1997, vol. 66, pp. 903-913.
[2] X. Gourdon, P. Sebah, “N-th digit computation”, preprint, 2003, http://numbers.computation.free.fr/Constants/Algorithms/nthdigit.pdf.
[3] D. E. Knuth, “The Art of Computer Programming. Vol. 2: Seminumerical Algorithms”, Addison-Wesley, Reading, MA, 1981.
Retour à la page d'accueil

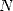 -ième digit d’un nombre
-ième digit d’un nombre  sans connaitre les précédents
sans connaitre les précédents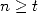 , alors
, alors 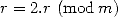 ;
; 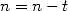 ; FinSi
; FinSi
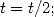
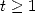 alors
alors 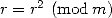 ; Aller à l’étape 1. ; FinSi.
; Aller à l’étape 1. ; FinSi.