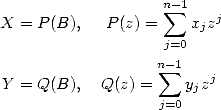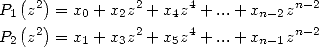|
|
|
|
|


Multiplication rapide par FFT
2 L’algorithme de multiplication rapide de deux grands entiers par FFT
References
1 Retour à l’école
Si l’on vous demande de multiplier 32*14 dans votre tête, comment allez-vous faire ? Sans doute, tout en vous rappelant douloureusement des règles enseignées a l’école primaire, utiliser 32=3*10+2, 14=10+4, puis multiplier membre à membre, gérer les retenues et tout ça. Ouf, ça parait le plus simple... Mais est-ce vraiment le plus simple ? Question bizarre, n’est-ce pas ? Depuis l’avènement des machines à calculer, c’est à dire la fin des années 40, le manque
d’algorithme de multiplication efficace oblige à segmenter chaque nombre en tranches, par exemple
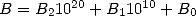 comme à l’école. La multiplication de nombres de taille
comme à l’école. La multiplication de nombres de taille 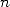 nécessite alors un
temps (ou nombre d’opérations) proportionnel à
nécessite alors un
temps (ou nombre d’opérations) proportionnel à 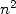 sans compter l’utilisation mémoire proportionnelle à
sans compter l’utilisation mémoire proportionnelle à 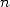 .
Afin de conserver le rythme de progression du record de calcul de décimales de
.
Afin de conserver le rythme de progression du record de calcul de décimales de 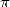 au cours des années 50
(voir pages Histoire ou Décimales), des améliorations théoriques et algorithmiques semblent nécessaires.
C’est alors à cette époque que les choses s’accélèrent.
au cours des années 50
(voir pages Histoire ou Décimales), des améliorations théoriques et algorithmiques semblent nécessaires.
C’est alors à cette époque que les choses s’accélèrent.
En 1965, Cooley and Tukey introduisent sous sa forme moderne une méthode de réduction de la
complexité du calcul des séries de Fourier connue aujourd’hui sous le nom de Transformée de Fourier Rapide
[1]. Il semble que Gauss ait déjà deviné l’astuce de la factorisation critique dès 1805. Quel génie, celui-là...
Quoi qu’il en soit, Schönhage et Strassen en tirent un algorithme de multiplication de grands
entiers en compexité 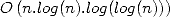 ce qui est considérablement mieux que
ce qui est considérablement mieux que 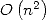 [2]
!
[2]
!
Cette page explique le fonctionnement de cet algorithme de multiplication rapide de deux grands entiers
par FFT, qui a tant fait pour le calcul des décimales de 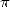 ! Pour les ordis, c’est bien... Mais pour nous,
finalement, euh... ce n’est pas si naturel !
! Pour les ordis, c’est bien... Mais pour nous,
finalement, euh... ce n’est pas si naturel !
2 L’algorithme de multiplication rapide de deux grands entiers par FFT
Soient X et Y deux grands entiers de taille 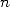 en base
en base 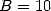 usuellement (ou une puissance de
usuellement (ou une puissance de
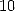 ).
).
2.1 Décomposition polynomiale
On écrit 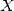 et
et 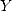 sous forme polynomiale en les décomposant (de manière unique) dans la base
sous forme polynomiale en les décomposant (de manière unique) dans la base
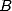
où 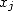 et
et 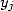 sont donc respectivement les
sont donc respectivement les 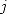 -ème décimales de
-ème décimales de 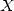 et
et 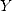 (
(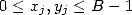 ). Cette
opération est de complexité à peu près proportionnelle à
). Cette
opération est de complexité à peu près proportionnelle à 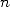 . On cherche maintenant à effectuer
“rapidement” la multiplication
. On cherche maintenant à effectuer
“rapidement” la multiplication 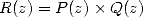 puis à évaluer à la fin
puis à évaluer à la fin 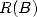 .
. 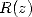 est
polynôme de degré
est
polynôme de degré 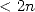 et peut être retrouvé par interpolation à partir de son évaluation en
et peut être retrouvé par interpolation à partir de son évaluation en
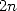 points, autrement dit par l’évaluation de
points, autrement dit par l’évaluation de 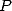 et
et 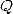 en ces mêmes
en ces mêmes 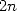 points. Le choix des
points, c’est la finesse de l’algorithme ! On utilise les racines primitives
points. Le choix des
points, c’est la finesse de l’algorithme ! On utilise les racines primitives 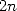 -ième de l’unité, i.e.
les
-ième de l’unité, i.e.
les
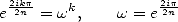 | (3) |
car cette évaluation (qui n’est alors rien d’autre que le calcul d’une série de Fourier) peut être réalisée en
complexité 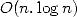 si
si 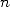 est une puissance de
est une puissance de  et avec un peu d’astuce. C’est la Transformée de
Fourier Rapide ou FFT en anglais.
et avec un peu d’astuce. C’est la Transformée de
Fourier Rapide ou FFT en anglais.
2.2 Transformée de Fourier rapide
En conservant les notations précédentes, évaluons le polynôme 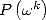 et
et 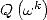 en se plaçant sous
l’hypothèse que
en se plaçant sous
l’hypothèse que 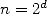 . Posons
. Posons
et 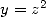 . On obtient alors
. On obtient alors
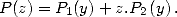 | (6) |
Maintenant, il faut se rappeler que puisque 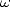 est une racine
est une racine 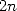 -ième de l’unité, alors pour
-ième de l’unité, alors pour
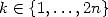
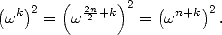 | (7) |
En conséquence, évaluer 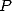 aux racines
aux racines 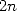 -ièmes de l’unité revient à évaluer
-ièmes de l’unité revient à évaluer 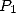 et
et 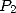 chacun aux
chacun aux 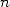 points
points 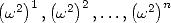 et à reporter les résultats dans
et à reporter les résultats dans 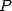 à l’aide de l’équation 6. Si
à l’aide de l’équation 6. Si 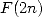 est le
nombre d’opérations élémentaires (addition, multiplication) requises pour évaluer
est le
nombre d’opérations élémentaires (addition, multiplication) requises pour évaluer 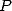 en
en 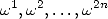 alors en vertu du principe précédent et de 6, on a
alors en vertu du principe précédent et de 6, on a
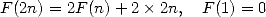 | (8) |
où le terme 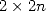 provient des dernières addition et multiplication requises pour obtenir
provient des dernières addition et multiplication requises pour obtenir 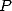 à partir de
à partir de
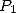 et
et 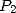 dans 6.
dans 6.
Comme 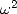 est une racine primitive
est une racine primitive 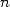 -ième de l’unité, on peut réappliquer le même procédé pour
chaque polynôme
-ième de l’unité, on peut réappliquer le même procédé pour
chaque polynôme 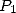 et
et 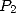 . Par suite, comme
. Par suite, comme 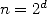 est une puissance de
est une puissance de  , le processus (et donc 6)
s’itère encore
, le processus (et donc 6)
s’itère encore 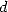 fois. On obtient finalement un nombre d’opérations
fois. On obtient finalement un nombre d’opérations
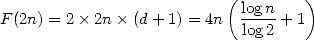 | (9) |
d’où la complexité en 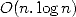 de la FFT. De même pour la FFT inverse, qui utilise
de la FFT. De même pour la FFT inverse, qui utilise 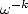 au lieu de
au lieu de
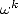 .
.
2.3 Interpolation
Nous avons maintenant calculé nos 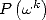 et
et 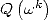 pour
pour 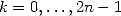 . On forme les
. On forme les 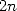 produits
produits
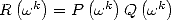 qui reviennent à des multiplications élémentaires puisque
qui reviennent à des multiplications élémentaires puisque 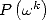 est forcément de
module inférieur à
est forcément de
module inférieur à 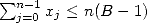 d’après 1, de même pour
d’après 1, de même pour 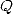 . Comme l’on cherche à retrouver
. Comme l’on cherche à retrouver
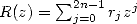 , il faut l’interpoler à partir des
, il faut l’interpoler à partir des 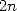 valeurs
valeurs 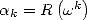 . Autrement dit, on cherche à
résoudre le système
. Autrement dit, on cherche à
résoudre le système
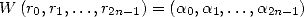 | (10) |
où
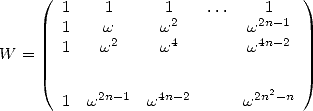 | (11) |
ce qui est équivalent à
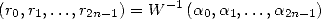 | (12) |
où 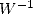 a la bonne idée d’être simple
a la bonne idée d’être simple
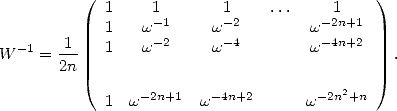 | (13) |
Le calcul de 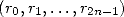 n’est donc rien d’autre que le conjugué de la transformée de Fourier de
n’est donc rien d’autre que le conjugué de la transformée de Fourier de
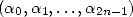 , autrement dit sa transformée de Fourier inverse, dont on a vu qu’elle est en
, autrement dit sa transformée de Fourier inverse, dont on a vu qu’elle est en 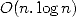 comme la FFT. On obtient alors
comme la FFT. On obtient alors 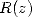 d’où l’on tire
d’où l’on tire 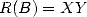 . Cette dernière opération est à peu près
en complexité
. Cette dernière opération est à peu près
en complexité 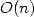 car les
car les 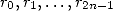 sont déjà proches des décimales de
sont déjà proches des décimales de 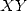 , aux
retenues près (dès que
, aux
retenues près (dès que 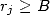 ). Toutes les retenues sont en fait calculées simultanément, puis
reportées, puis on recalcule les éventuelles nouvelles retenues créées, etc... (opération appelée
vectorisation).
). Toutes les retenues sont en fait calculées simultanément, puis
reportées, puis on recalcule les éventuelles nouvelles retenues créées, etc... (opération appelée
vectorisation).
La combinaison de tous ces algorithmes et quelques menus raffinements selon les programmeurs
permettent d’atteindre à peu près la borne optimale théorique de Schönhage et Strassen pour la FFT en
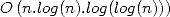 .
.
References
[1] J. W. Cooley, J. W. Tukey, “An algorithm for the machine calculation of complex Fourier series”, Math. Comp. 1965, vol 19, pp. 297-301.
[2] A. Schönhage, V. Strassen, “Schennelle Multiplikation grosser Zahlen”, Computing, 1971, vol. 7, pp. 281-292.
Retour à la page d'accueil