Archimède
(287 av. J.-C. - 212 av. J.-C.)

Application de la méthode d'Archimède :

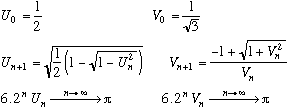
Tranches de vie :

Archimède est né aux environs de 287 av. J.-C. Considéré par tous comme le plus grand mathématicien et physicien de toute l'antiquité (et c'est justifié !), la légende qui l'entoure et les écrits qui nous sont parvenus sont en effet assez impressionnants. De l'équilibre des plans, Sur la sphère et le cylindre, l'Arénaire - où Archimède expose un système de numérotation des grands nombres (calcul du nombre de grains de sable contenus dans la sphère du monde !) - , Traité de la méthode , sont autant d'écrits brillants. Sans oublier bien sûr Des corps flottants - et son fameux principe d'Archimède - , et la Mesure du cercle. Dans ce dernier ouvrage qui nous intéresse, Archimède exhibe l'encadrement célèbre

Conduisant la défense de Syracuse contre les Romains (on lui attribue, mais la polémique est vive, d'avoir pu incendier à distance la flotte de Marcellus au moyen d'un jeu de miroirs...) et malgré les ordres de protection du général romain, il est assassiné par un légionnaire lors de la prise de la ville en 212 av. J.-C.
Et pour quel motif, me direz-vous ? Eh bien, d'après la légende, Archimède était en train de dessiner une figure sur le sol, et dit au romain qui entrait de ne pas le déranger. Ce dernier, vexé, l'aurait transpercé de sa lance. Mais la richesse de l'intérieur d'Archimède y fut peut-être aussi pour quelque chose...

Autour de

Archimède n'a bien sûr jamais eu sous les yeux la formule ci-dessus, il ne connaissait pas la trigonométrie, d'ailleurs ! Néanmoins, celle-ci n'est qu'une écriture moderne de sa méthode d'approximation de .
Eh oui, ce bon vieux Archimède fut en effet le premier à calculer véritablement ses décimales au moyen d'un algorithme. Il partit de 2 polygones à 6 côtés inscrits et circonscrits à un cercle de rayon R=1/2. En faisant doubler à chaque fois le nombre de côtés des polygones, ces derniers allaient finir par se confondre avec le cercle, et leur périmètre allait tendre vers celui du cercle, soit 2R=. Brillante idée qui prévaudra jusqu'au XVIIe siècle dans le calcul des décimales !
C'est surtout sa méthode qui prévaudra, et celle-ci sera transcrite de différentes manières en écriture algorithmique, dont celle-ci (voir aussi Cues, Al Kashi, Viète); C'est pourquoi on ne sait jamais vraiment de qui proviennent les algorithmes partant de l'idée d'Archimède. J'ai choisi celui-ci, mais cela aurait pu être celui de Cues.
Archimède obtint son encadrement avec un polygone à 96 côtés (n=4 dans la formule).

Démonstration

On considère un cercle de rayon 1 et un angle . Posons . U_n représente la longueur d'un côté du polygone inscrit au cercle et V_n celle d'un côté du polygone circonscrit au cercle.
par développements limités en 0, donc on a immédiatement le résultat de la formule en haut de la page.

Ce raisonnement d'analyse pure se traduisait géométriquement pour Archimède par le fait que le polygone à 6.2 ⁿ côtés tend à se confondre avec le cercle lorsque n tend vers l'infini. Reste à ce que les U_n et V_n aient la même forme que dans la formule...
Pour cela, il suffit de chercher une formule de récurrence entre U_n+1 et U_n (positifs) d'une part, et entre V_n+1 et V_n (positifs aussi) d'autre part.
A partir de cos²x+sin²x=1 et cos(2x)=1-2sin²x, on obtient ce qui donne la relation .
De même, on a , donc en posant X=, on a le trinôme du second degré en X
tan(x)X² +2X-tan(x)=0. La solution positive donne X=tan(x/2)= d'où l'on tire alors pour tout n entier positif . La valeur de U₀ et V₀ s'obtient par les expressions premières de U_n et V_n.

Essais

P'tite note sur les essais : Ceux-ci sont simplement une meilleure façon de sentir les performances d'une suite. Pour être clair, j'utiliserai une notation un peu personnelle mais tellement pratique ! Lorsque l'on trouvera une convergence "d'environ 3n/5" comme ici, cela voudra dire que l'on aura à peu près 3n/5 décimales justes au rang n. Cela n'a rien à voir avec une "convergence en n*log(n)" par exemple qui veut dire que le temps de calcul de n décimales est proportionnel à n*log(n).
Le chiffre entre parenthèses indique le nombre de décimales justes.

U1=3,10582 (1)	V1=3,21539 (0)
U4=3,14103 (3)	V4=3,14271 (2) (encadrement d'archimède)
U10=3,14159251 (6)	V10=3,14159296 (6)

On observe une convergence d'environ 3n / 5 pour les 2 suites ce qui est très honorable par rapport aux suites à convergence logarithmique (Wallis, Stirling...). Ceci explique sans doute aussi que cette méthode ait prévalu aussi longtemps pour calculer les décimales de (oh, juste quelques temps, 20 siècles (!), jusqu'à la découverte de la formule de Machin en 1706).

Accélération de la convergence

Comme dans à peu près chaque page web de mathématiciens de ce site, on trouvera un chapitre consacré à l'accélération par le Delta2 d'Aitken, tant cette formule est efficace et simple à appliquer (enfin presque...)
Pour n=5, on a U₅=3,14145 (3) et t₅=3,1415926836 (7).
Impressionnant, on gagne 4 décimales, en fait, on double la rapidité de convergence, ce qui est beaucoup plus économique que de calculer les 6 itérations de U_n supplémentaires dont nous aurions besoin sinon pour obtenir le même nombre de décimales...
Pour n=7, on a U₇=3,141583 (4) et t₇=3,14159265370 (9).
(ne nous enflammons pas trop, rappelons néanmoins que le Delta2 est très sensible aux imprécisions...)