|
|
|
|
|
Table des matières
1 Petit rappel historique rapide
2 Introduction aux séries hypergéométriques
2.1 Définition
2.2 Quelques propriétés et exemples simples
3 La fonction Psi : Base des formules type Machin ou BBP
3.1 Définition
3.2 Equations différentielles
4 Formule de type Machin
5 Formules BBP : La technique
5.1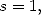
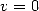 : Les polylogarithmes
: Les polylogarithmes
5.1.1 Définition
5.1.2 Valeurs remarquables
5.1.3 Formule de duplication
5.1.4 Formules d’Euler et de Landen pour le dilogarithme
5.1.5 Formule de Landen pour le trilogarithme
5.1.6 Valeurs particulières
5.1.7 Quelques intégrales classiques
5.2 Liens entre intégrales, formules BBP et polylogarithmes
5.2.1 Notations
5.3 Intégrales et formules BBP
5.3.1 Intégrales équivalentes aux séries BBP
5.3.2 Intégrales plus générales et formules BBP
5.3.3 Calcul des intégrales
5.4 Fonction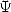 et polylogarithmes
et polylogarithmes
5.5 Intérêt des formules BBP
6 Formules BBP en base 2 :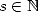 ,
,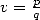 ,
, 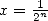 dans
dans 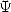
6.1 Les intégrales considérées
6.2 La méthode
6.3 Formules pour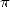 ,
, 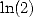 ,
, 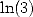 et
et 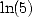
6.3.1 Application aux formules BBP pour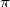
6.3.2 Formules BBP pour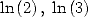 et
et 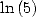
6.4 Cas des polylogarithmes d’ordre : Formules d’ordre 2
: Formules d’ordre 2
6.4.1 Les expressions classiques :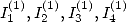 et
et 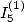
6.4.2 Calcul de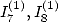 et
et 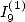
6.4.3 Calcul de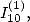 relation entre
relation entre 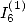 et
et 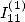
6.4.4 Application à la détermination de formules BBP
6.4.5 Quelques formules composites
6.5 Cas des polylogarithmes d’ordre 3
6.5.1 Calcul de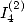
6.5.2 Calcul de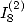
6.5.3 Relation entre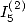 et
et 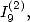 valeur de
valeur de 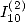
6.5.4 Calcul de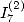
6.5.5 Application à la détermination de formules BBP
6.6 Cas des polylogarithmes d’ordre 4
6.6.1 Les relations
6.6.2 Application à la détermination de formules BBP
6.6.3 Formules pour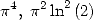 et
et 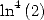
6.7 Cas des polylogarithmes d’ordre 5
6.7.1 Les relations
6.7.2 Application à la détermination de formules BBP
6.7.3 Formules pour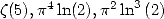 et
et 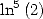
6.7.4 Simplifications de ces formules
7 entier fixé,
entier fixé,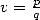 ,
, 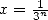 : BBP en base 3
: BBP en base 3
7.1 Formules pour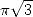
7.2 Formules d’ordre 2 : intégrales avec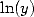
7.3 Formules d’ordre 3 : Intégrales avec ln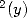
8 Et les autres bases alors ? ?
9 Polygamma et Clausen
9.1 Fonctions polygamma
9.2 La fonction digamma
9.3 Polygamma d’ordre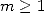
9.3.1 Liens avec les intégrales des formules BBP
9.3.2 Une approche graphique
9.3.3 Traduction analytique
9.4 Combinaisons de Kölbig
9.4.1 Fonctions de Clausen
9.4.2 Les résultats de Kölbig.
10 Introduction de factorielles et combinaisons
10.1 Un premier exemple
10.2 Umbral calculus
11 Séries binomiales centrales
11.1 Inversion de combinaisons
11.2 Développements utiles
11.3 Premières formules directes
11.4 Formules d’ordre supérieur
11.4.1 Une première formule avec démo
11.4.2 Calcul d’une primitive de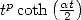
11.4.3 Utilisation de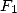
11.4.4 Utilisation de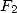
11.4.5 D’autres formules
12 Autres coefficients binomiaux
12.1 Formules primitives
12.2 Formules factorielles polynômiales
12.3 Alors, que dire de tout cela ?
12.4 Démonstrations
12.5 Combinaisons rapides : Formules factorielles BBP
12.6 Alors, que dire de tout cela ?
12.7 Démonstration typique
12.7.1 La méthode
12.7.2 Application : La démo de la première formule
12.7.3 Démo de la formule en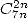
12.7.4 Prédiction des formules
12.8 Produit de combinaisons
13 Séries harmoniques
13.1 Proximité des séries harmoniques et des polylogarithmes
13.2 Etude de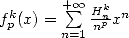 et de
et de 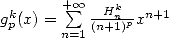
13.2.1 Définition, relations remarquables
13.2.2 Calcul de certaines fonctions
13.3 Application au calcul de certaines séries
13.3.1 Avec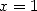
13.3.2 Avec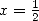
13.3.3 Avec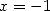
13.3.4 Avec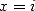
13.3.5 Avec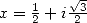
13.3.6 Avec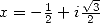
13.3.7 Avec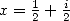
13.4 Généralisations
13.4.1 Sommes d’Euler
13.4.2 Une formule combinant Harmoniques et combinatoire
13.4.3 Une autre formule
13.4.4 Harmoniques d’harmoniques !
14 Séries de factorielles supérieures : Ramanujan, Borwein, Chudnovsky....
14.1 Coefficients binomiaux centraux au carré : Formules elliptiques
14.2 Coefficients binomiaux centraux au cube : Identité de Ramanujan
15 Autres formules hypergéométriques concernant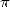
2 Introduction aux séries hypergéométriques
2.1 Définition
2.2 Quelques propriétés et exemples simples
3 La fonction Psi : Base des formules type Machin ou BBP
3.1 Définition
3.2 Equations différentielles
4 Formule de type Machin
5 Formules BBP : La technique
5.1
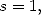
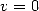 : Les polylogarithmes
: Les polylogarithmes
5.1.1 Définition
5.1.2 Valeurs remarquables
5.1.3 Formule de duplication
5.1.4 Formules d’Euler et de Landen pour le dilogarithme
5.1.5 Formule de Landen pour le trilogarithme
5.1.6 Valeurs particulières
5.1.7 Quelques intégrales classiques
5.2 Liens entre intégrales, formules BBP et polylogarithmes
5.2.1 Notations
5.3 Intégrales et formules BBP
5.3.1 Intégrales équivalentes aux séries BBP
5.3.2 Intégrales plus générales et formules BBP
5.3.3 Calcul des intégrales
5.4 Fonction
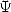 et polylogarithmes
et polylogarithmes
5.5 Intérêt des formules BBP
6 Formules BBP en base 2 :
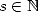 ,
,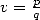 ,
, 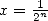 dans
dans 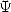
6.1 Les intégrales considérées
6.2 La méthode
6.3 Formules pour
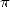 ,
, 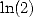 ,
, 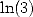 et
et 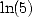
6.3.1 Application aux formules BBP pour
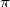
6.3.2 Formules BBP pour
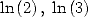 et
et 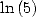
6.4 Cas des polylogarithmes d’ordre
 : Formules d’ordre 2
: Formules d’ordre 2
6.4.1 Les expressions classiques :
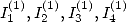 et
et 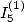
6.4.2 Calcul de
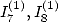 et
et 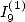
6.4.3 Calcul de
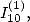 relation entre
relation entre 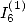 et
et 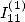
6.4.4 Application à la détermination de formules BBP
6.4.5 Quelques formules composites
6.5 Cas des polylogarithmes d’ordre 3
6.5.1 Calcul de
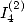
6.5.2 Calcul de
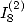
6.5.3 Relation entre
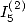 et
et 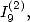 valeur de
valeur de 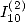
6.5.4 Calcul de
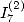
6.5.5 Application à la détermination de formules BBP
6.6 Cas des polylogarithmes d’ordre 4
6.6.1 Les relations
6.6.2 Application à la détermination de formules BBP
6.6.3 Formules pour
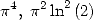 et
et 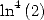
6.7 Cas des polylogarithmes d’ordre 5
6.7.1 Les relations
6.7.2 Application à la détermination de formules BBP
6.7.3 Formules pour
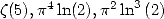 et
et 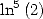
6.7.4 Simplifications de ces formules
7
 entier fixé,
entier fixé,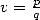 ,
, 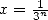 : BBP en base 3
: BBP en base 3
7.1 Formules pour
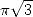
7.2 Formules d’ordre 2 : intégrales avec
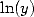
7.3 Formules d’ordre 3 : Intégrales avec ln
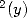
8 Et les autres bases alors ? ?
9 Polygamma et Clausen
9.1 Fonctions polygamma
9.2 La fonction digamma
9.3 Polygamma d’ordre
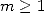
9.3.1 Liens avec les intégrales des formules BBP
9.3.2 Une approche graphique
9.3.3 Traduction analytique
9.4 Combinaisons de Kölbig
9.4.1 Fonctions de Clausen
9.4.2 Les résultats de Kölbig.
10 Introduction de factorielles et combinaisons
10.1 Un premier exemple
10.2 Umbral calculus
11 Séries binomiales centrales
11.1 Inversion de combinaisons
11.2 Développements utiles
11.3 Premières formules directes
11.4 Formules d’ordre supérieur
11.4.1 Une première formule avec démo
11.4.2 Calcul d’une primitive de
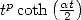
11.4.3 Utilisation de
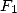
11.4.4 Utilisation de
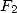
11.4.5 D’autres formules
12 Autres coefficients binomiaux
12.1 Formules primitives
12.2 Formules factorielles polynômiales
12.3 Alors, que dire de tout cela ?
12.4 Démonstrations
12.5 Combinaisons rapides : Formules factorielles BBP
12.6 Alors, que dire de tout cela ?
12.7 Démonstration typique
12.7.1 La méthode
12.7.2 Application : La démo de la première formule
12.7.3 Démo de la formule en
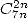
12.7.4 Prédiction des formules
12.8 Produit de combinaisons
13 Séries harmoniques
13.1 Proximité des séries harmoniques et des polylogarithmes
13.2 Etude de
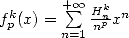 et de
et de 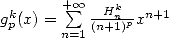
13.2.1 Définition, relations remarquables
13.2.2 Calcul de certaines fonctions
13.3 Application au calcul de certaines séries
13.3.1 Avec
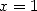
13.3.2 Avec
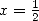
13.3.3 Avec
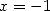
13.3.4 Avec
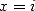
13.3.5 Avec
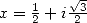
13.3.6 Avec
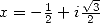
13.3.7 Avec
13.4 Généralisations
13.4.1 Sommes d’Euler
13.4.2 Une formule combinant Harmoniques et combinatoire
13.4.3 Une autre formule
13.4.4 Harmoniques d’harmoniques !
14 Séries de factorielles supérieures : Ramanujan, Borwein, Chudnovsky....
14.1 Coefficients binomiaux centraux au carré : Formules elliptiques
14.2 Coefficients binomiaux centraux au cube : Identité de Ramanujan
15 Autres formules hypergéométriques concernant
Retour à la page d'accueil
