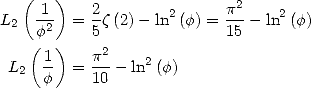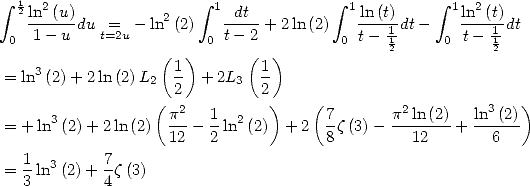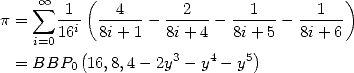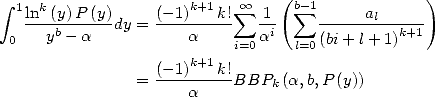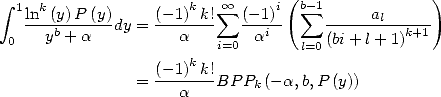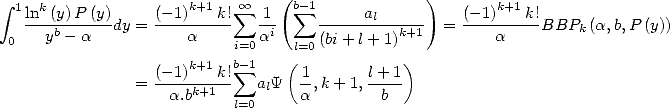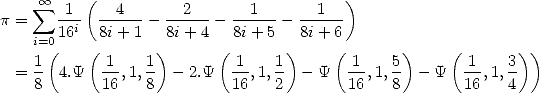|
|
|
|
|
5 Formules BBP : La technique
 En 1995, Bailey, Borwein et Plouffe découvrent la fameuse formule
En 1995, Bailey, Borwein et Plouffe découvrent la fameuse formule
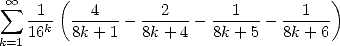 | (B.B.P.) |
qui, comme on le sait maintenant, va bien au-delà de sa forme simple en proposant une méthode pour atteindre le n-ième digit de Pi sans connaitre les précédents. Mieux, elle révolutionne la vision de Pi en l’inscrivant parmi les constantes dont on peut générer les décimales quasiment comme un système dynamique chaotique, ce que Bailey et Crandall ont traduit par leur célèbre conjecture de l’an 2000 [11] reliant le concept de normalité à celui de passage d’un digit au suivant.
En plus de la fonction 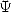 , assez rapidement, on se rendra compte que les formules BBP sont un cas particuliers de relations d’une classe
de fonctions que l’on appelle les polylogarithmes. Une jolie introduction à ces fonctions extraordinairement simples mais prometteuses est
l’oeuvre de Gery Huvent que j’adapte ici :
, assez rapidement, on se rendra compte que les formules BBP sont un cas particuliers de relations d’une classe
de fonctions que l’on appelle les polylogarithmes. Une jolie introduction à ces fonctions extraordinairement simples mais prometteuses est
l’oeuvre de Gery Huvent que j’adapte ici :
5.1 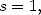
 : Les polylogarithmes
: Les polylogarithmes
5.1.1 Définition
Pour 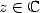 ,
,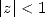 et
et 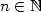 , on définit le polylogarithme d’ordre
, on définit le polylogarithme d’ordre 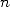 par
par
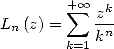 | (32) |
Ainsi
Pour 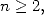 signalons que la convergence est normale sur le disque unité fermé.
signalons que la convergence est normale sur le disque unité fermé.
On dispose de la représentation intégrale suivante
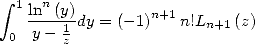 | (35) |
qui permet de prolonger le polylogarithme, pour 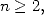 sur
sur ![C\]1,+ oo [](../mathematiciens/huvent/hyperg190x.gif) en une fonction holomorphe.
en une fonction holomorphe.
Les polylogarithmes peuvent également être définies par des intégrations successives, en effet
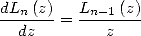 | (36) |
ainsi
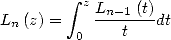 | (37) |
et par exemple
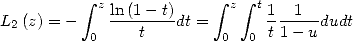 | (38) |
5.1.2 Valeurs remarquables
Les premières valeurs remarquables sont pour
pour 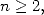
où 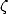 est la fonction zéta de Riemann
est la fonction zéta de Riemann
En particulier
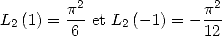 | (Euler) |
Pour 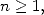
où 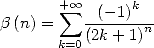 . En particulier
. En particulier
Remarque 1 On connaît la valeur exacte de 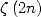 et de
et de 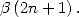
5.1.3 Formule de duplication
On a sur ![C\]1,+o o [](../mathematiciens/huvent/hyperg206x.gif) ,
, 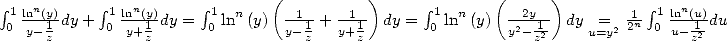 . Ce qui prouve
la formule de duplication, lorsque les trois termes ont un sens :
. Ce qui prouve
la formule de duplication, lorsque les trois termes ont un sens :
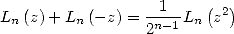 | (45) |
5.1.4 Formules d’Euler et de Landen pour le dilogarithme
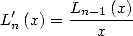 | (46) |
Cette égalité permet de prouver par dérivation l’identité d’Euler pour le dilogarithme
![A x (- ]0,1[, L2(x)+ L2(1 -x) = z(2)- ln (1 - x)ln (x)](../mathematiciens/huvent/hyperg211x.gif) | (47) |
En particulier avec 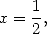 on obtient le résultat suivant, dû à Euler
on obtient le résultat suivant, dû à Euler
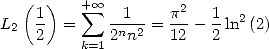 | (Euler) |
Formules de Landen On dispose également de la relation suivante dite identité de Landen (que l’on prouve par dérivation)
![[ ] ( )
A x (- - 1, 1 , L2 (x)+ L2-x-- = -1 ln2(1 -x)
2 x- 1 2](../mathematiciens/huvent/hyperg214x.gif) | (48) |
Cette identité se prolonge sur ![[ ]
C\RU -1, 12](../mathematiciens/huvent/hyperg215x.gif)
Valeurs particulières
Avec 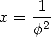 où
où 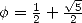 est le nombre d’or (qui vérifie
est le nombre d’or (qui vérifie 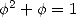 ), puisque
), puisque 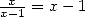 dans ce cas, on
obtient
dans ce cas, on
obtient
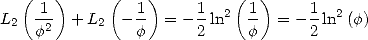 | (49) |
Mais la formule d’Euler fournit
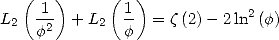 | (50) |
et le formule de duplication
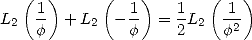 | (51) |
En combinant les trois résultats, on obtient
Valeurs complexes
L’identité de Landen se prolonge par analycité à ![C\]1,+o o [.](../mathematiciens/huvent/hyperg224x.gif) Avec
Avec 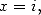 on obtient
on obtient
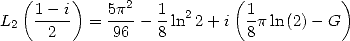 | (54) |
5.1.5 Formule de Landen pour le trilogarithme
![] 1]
A x (- -1, 2](../mathematiciens/huvent/hyperg227x.gif)
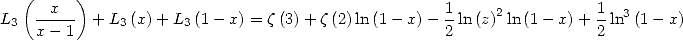 | (55) |
Cette formule se déduit des identités d’Euler et de Landen pour le dilogarithme après dérivation.
5.1.6 Valeurs particulières
On déduit de l’identité de Landen pour le trilogarithme les valeurs remarquables suivantes :
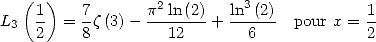 | (56) |
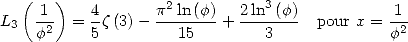 | (57) |
5.1.7 Quelques intégrales classiques
La représentation intégrale (35) donne immédiatement
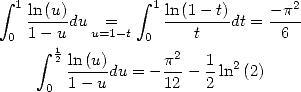 | (58) (59) |
De même
5.2 Liens entre intégrales, formules BBP et polylogarithmes
5.2.1 Notations
Commençons par simplifier les notations ! Il serait bon en effet de pouvoir parler d’une formule BBP sans à chaque fois recopier la formule...
Gery Huvent a ainsi proposé de noter 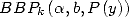 la somme
la somme 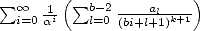 , pour
, pour
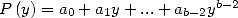 .
.
La formule de Plouffe s’écrit alors
Ca simplifie tout de même !
5.3 Intégrales et formules BBP
On se propose dans cette section de convenir des intégrales équivalentes aux séries BBP. Il est en effet souvent plus simple de passer par le calcul d’une intégrale pour trouver le résultat d’une série !
5.3.1 Intégrales équivalentes aux séries BBP
Ainsi, de l’égalité 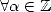 ,
, 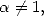 et
et 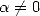 ,
, ![A y (- [0,1], A k > 1,](../mathematiciens/huvent/hyperg240x.gif)
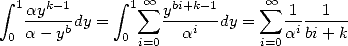 | (62) |
on déduit que si ![b- 2
P (- Qb-2 [X] , P = a0 + a1X + ...+ ab-2X](../mathematiciens/huvent/hyperg242x.gif) alors
alors
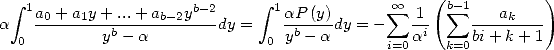 | (63) |
De la même manière,
5.3.2 Intégrales plus générales et formules BBP
Maintenant, l’on se doute bien que ce n’est pas forcément ce type d’intégrale que l’on saura calculer, et donc dont on pourra déduire des
formules BBP, mais on aura affaire plus sûrement à une intégrale du type 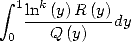 . Mais toute l’astuce est
là !
. Mais toute l’astuce est
là !
En effet, si 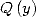 divise
divise 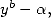
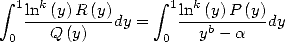 où
où 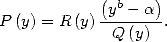 Ceci permet, lorsque l’on sait
calculer l’intégrale
Ceci permet, lorsque l’on sait
calculer l’intégrale 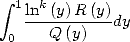 , d’en déduire une formule BBP. Le même type de remarque s’applique si
, d’en déduire une formule BBP. Le même type de remarque s’applique si 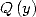 divise
divise
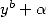 .
.
5.3.3 Calcul des intégrales
Maintenant, parlons des polylogarithmes. La remarque ci-dessus est valable dans le cas où 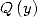 divise
divise 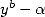 pour extraire des séries
BBP. Mais pour le calcul de l’intégrale ? Eh bien on peut avoir recours à une décomposition en éléments simples de
pour extraire des séries
BBP. Mais pour le calcul de l’intégrale ? Eh bien on peut avoir recours à une décomposition en éléments simples de 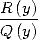 pour se ramener à
des intégrales connues. Et c’est là qu’interviennent les polylogarithmes.
pour se ramener à
des intégrales connues. Et c’est là qu’interviennent les polylogarithmes.
On rappelle l’expression intégrale du polylogarithme d’ordre 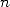 pour un complexe
pour un complexe  non nul de module inférieur à
non nul de module inférieur à
 .
.
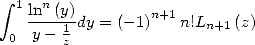 | (68) |
Ceci permet, après décomposition en éléments simples de 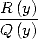 , d’exprimer une intégrale du type
, d’exprimer une intégrale du type 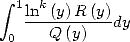 comme somme de
polylogarithmes.
comme somme de
polylogarithmes.
5.4 Fonction 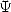 et polylogarithmes
et polylogarithmes
En plus de la relation évidente 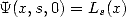 , le paragraphe précédent met en lumière que la décomposition d’une fraction rationnelle
, le paragraphe précédent met en lumière que la décomposition d’une fraction rationnelle
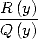 dans l’intégrale
dans l’intégrale 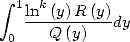 permet de se ramener d’une formule BBP à des polylogarithmes. Mais d’autre part,
la formule (64), dont on a vu le lien direct avec les formules BBP si l’on a un polynôme
permet de se ramener d’une formule BBP à des polylogarithmes. Mais d’autre part,
la formule (64), dont on a vu le lien direct avec les formules BBP si l’on a un polynôme 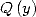 divisant
divisant 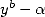 , s’écrit
également
, s’écrit
également
c’est-à-dire sous forme d’une combinaisons de fonctions 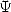 . En fait, les formules BBP ne sont rien d’autre que des combinaisons de
fonctions
. En fait, les formules BBP ne sont rien d’autre que des combinaisons de
fonctions 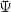 où le paramètre
où le paramètre  ne bouge pas et est une puissance inverse d’un entier.
ne bouge pas et est une puissance inverse d’un entier.
Ainsi, la formule de Plouffe s’écrit
A partir de là, et aux ordres supérieurs à 1 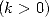 , nous avons tous les maillons pour faire correspondre les polylogarithmes avec les
formules BBP et maintenant les fonctions
, nous avons tous les maillons pour faire correspondre les polylogarithmes avec les
formules BBP et maintenant les fonctions 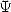 .
.
A ce stade, il faut remarquer que les polylogarithmes sont du style 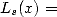
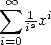 tandis que les formules BBP
utilisent plutôt des séries du type
tandis que les formules BBP
utilisent plutôt des séries du type 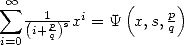 . Intuitivement, au lieu d’avoir le paramètre
. Intuitivement, au lieu d’avoir le paramètre 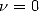 comme la
relation
comme la
relation 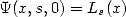 le laisse penser, les polylogarithmes vont pouvoir se ”développer” en fournissant des relations
linéaires entre fonctions
le laisse penser, les polylogarithmes vont pouvoir se ”développer” en fournissant des relations
linéaires entre fonctions 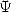 où
où 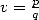 , bref des formules BBP. Dans cette présentation avec les paramètres de la fonction
, bref des formules BBP. Dans cette présentation avec les paramètres de la fonction
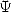 , on voit bien que c’est une sorte de généralisation des arctan puisque l’on n’a plus
, on voit bien que c’est une sorte de généralisation des arctan puisque l’on n’a plus 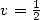 mais plus généralement
mais plus généralement
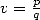 .
.
5.5 Intérêt des formules BBP
Cette formulation a permis de montrer que l’on pouvait en base 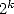 et
et 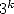 calculer n’importe quel digit des constantes résultats de ce type
de séries, sans connaitre les précédents. Pourquoi ? Je vous l’expliquerai un peu plus tard sur la page consacrée à Plouffe mais de manière
intuitive, on peut remarquer que le développement en base 10 d’un nombre
calculer n’importe quel digit des constantes résultats de ce type
de séries, sans connaitre les précédents. Pourquoi ? Je vous l’expliquerai un peu plus tard sur la page consacrée à Plouffe mais de manière
intuitive, on peut remarquer que le développement en base 10 d’un nombre 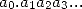 est
est 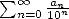 avec
avec 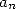 entier entre 0 et 9. Donc
en considérant des séries du genre
entier entre 0 et 9. Donc
en considérant des séries du genre 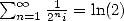 on n’est pas loin du développement en base 2 ! il suffit de pouvoir calculer les décimales
à un certain endroit de
on n’est pas loin du développement en base 2 ! il suffit de pouvoir calculer les décimales
à un certain endroit de  .
.
Et c’est ce qu’il s’est passé non seulement avec 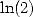 mais aussi plein d’autres constantes autour de
mais aussi plein d’autres constantes autour de  , la fonction
, la fonction  de Riemann
etc...
de Riemann
etc...
En outre, on pourra remarquer que ce sont des séries rationnelles et donc en tant que telles des proies idéales pour un calcul simple des
décimales de Pi. On sait de plus immédiatement grâce au terme 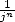 de la série combien de décimales on peut obtenir en pratique avec n
termes de la série. En fait, avec
de la série combien de décimales on peut obtenir en pratique avec n
termes de la série. En fait, avec 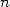 décimales, dans ce cas on obtient
décimales, dans ce cas on obtient 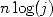 décimales (et même un peu plus compte tenu des termes en
décimales (et même un peu plus compte tenu des termes en
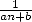 ).
).
Alternant des phases d’intensives explorations avec des phases plus calmes, la recherche dans cette direction a été fertile ! Quelques éléments dans les paragraphes qui suivent.
De manière synthétique, Gery Huvent a mis en avant quelques intégrales utiles à la décomposition dont le paragraphe précédent parle. Nous les présentons ici, avec leurs applications à la recherche de formules BBP. Ce texte reprend à quelques adaptations près l’article de Gery Huvent [12] qui est on ne peut plus fondamental !
Retour à la page d'accueil

![]- 1,1[,](../mathematiciens/huvent/hyperg209x.gif) on a
on a