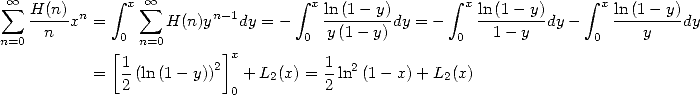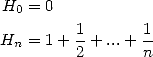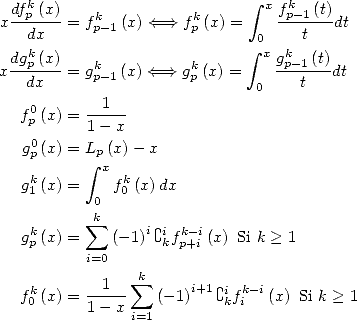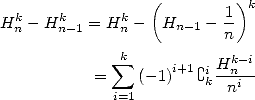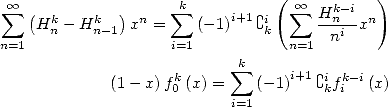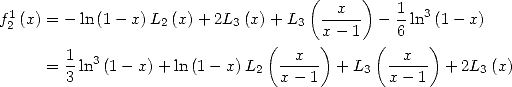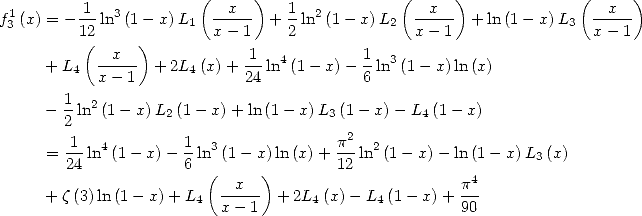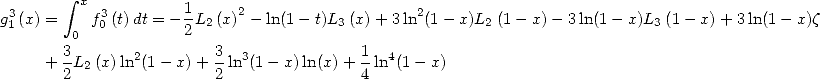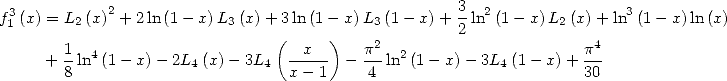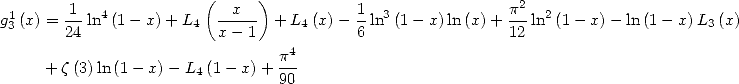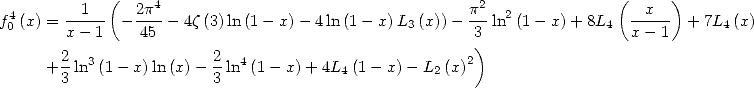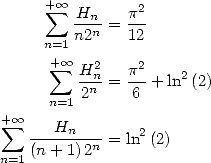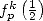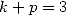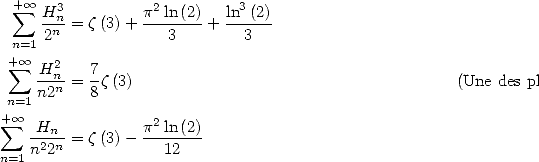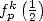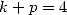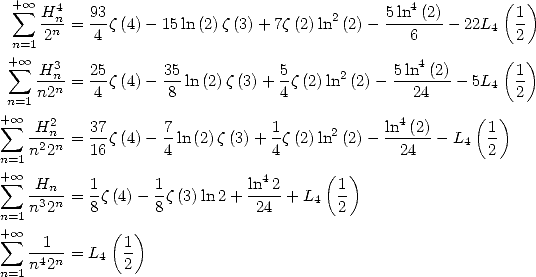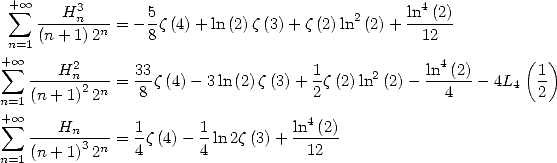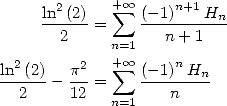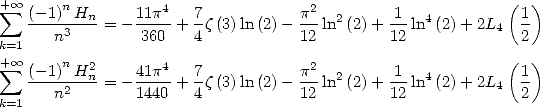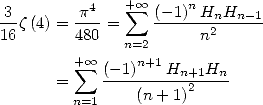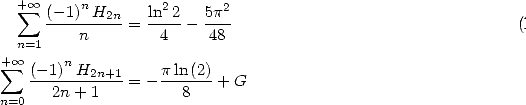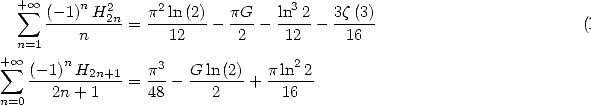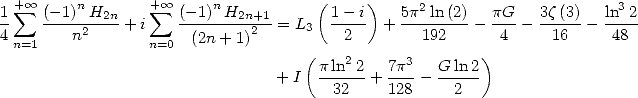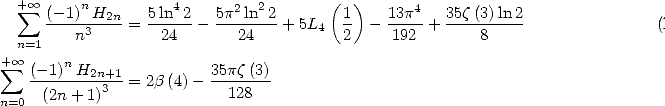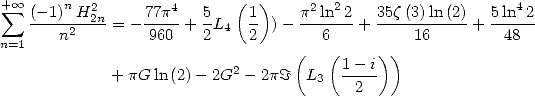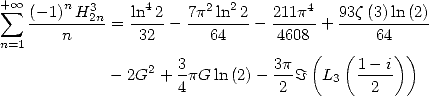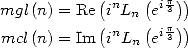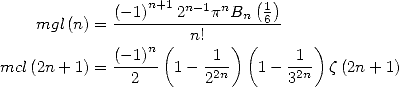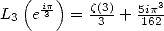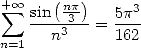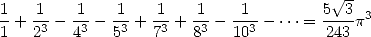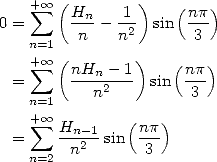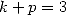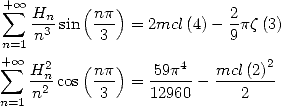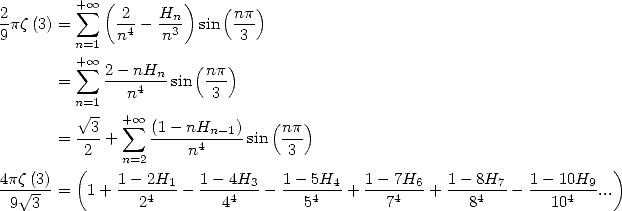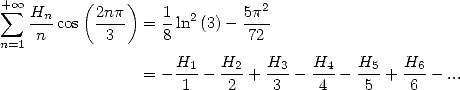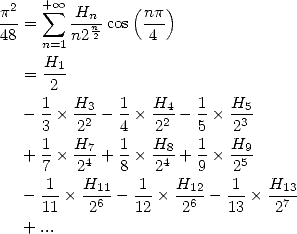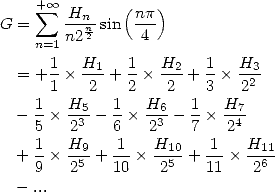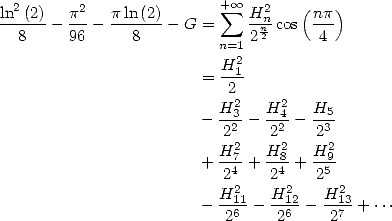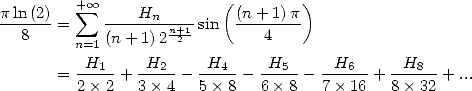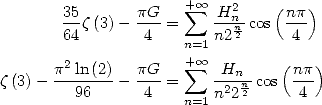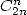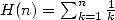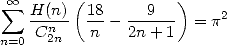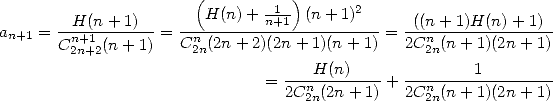|
|
|
|
|
13 Séries harmoniques
Les formules BBP s’expriment par exemple comme combinaisons linéaires de cette fonction hypergéométrique mais bien plus de choses nous attendent en fait ! Car grâce aux représentations intégrales, on peut en fait également obtenir des séries harmoniques de même forme que toutes celles que l’on vient de trouver.
Les séries harmoniques sont celles dont le terme contient la somme harmonique 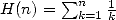 .
.
13.1 Proximité des séries harmoniques et des polylogarithmes
Nous avons vu que les formules BBP ou factorielles sont des combinaisons d’intégrales du type 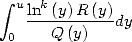 .
.
Considérons maintenant l’intégrale équivalente à la série de terme la somme harmonique 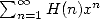 . D’après la formule du produit
de Cauchy selon laquelle pour des séries absolument convergentes
. D’après la formule du produit
de Cauchy selon laquelle pour des séries absolument convergentes 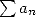 et
et 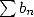
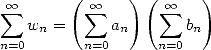 | (587) |
où 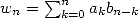 , en choisissant
, en choisissant 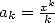 et
et 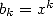 on obtient
on obtient 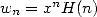 et donc
et donc
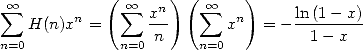 | (588) |
Vous commencez à voir ce que je veux dire... :-) Dès qu’une intégrale utilisera ce genre de formule, on aura de l’hamonique dans le coin.
Ici, on a immédiatement en 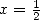 la formule
la formule
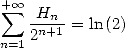 | (589) |
Avec 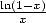 on avait du polylogarithme (voir 35), qu’à cela ne tienne, on divise par
on avait du polylogarithme (voir 35), qu’à cela ne tienne, on divise par  l’expression 588 ! Et en intégrant ensuite entre
l’expression 588 ! Et en intégrant ensuite entre
 et
et 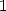 , on a
, on a
 Or, comme
Or, comme 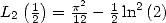 , on obtient finalement que
, on obtient finalement que
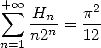 | (591) |
Fort, non ? évidemment, cela rappelle beaucoup de choses, on nage en pleins polylogarithmes et logarithmes...
On peut étudier plus généralement les séries harmoniques de ce type et les formules qui en découlent en introduisant les notations de Gery Huvent (encore lui !). Toutes les formules ci-dessous qui ne sont pas encore connues peuvent lui être attribuées !
13.2 Etude de 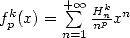 et de
et de 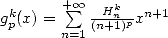
13.2.1 Définition, relations remarquables
On pose
Ces séries ont un rayon de convergence égal à 1. La convergence a lieu sur le bord dès que 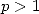 (car
(car 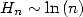 ). Alors
). Alors
Preuve.
donc
De même
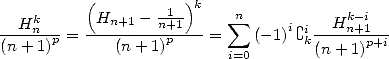 | (605) |
_
13.2.2 Calcul de certaines fonctions
Un développement usuel (faie le produit de Cauchy) donne
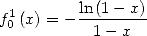 | (606) |
Puis par intégrations
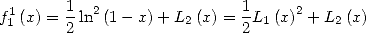 | (607) |
et
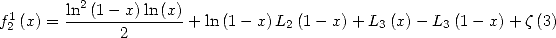 | (608) |
Avant de continuer, examinons cette égalité. Pour 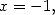 la série définissant
la série définissant 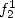 converge, mais le membre de droite de l’égalité
précédente ne l’est pas. Cependant avec les formules d’Euler et de Landen, on obtient
converge, mais le membre de droite de l’égalité
précédente ne l’est pas. Cependant avec les formules d’Euler et de Landen, on obtient
La dernière égalité nous donne une expression de 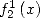 valable sur
valable sur ![[-1, 1]
2](../mathematiciens/huvent/hyperg1854x.gif) . Par prolongement analytique, on sait que les différentes
expresions obtenues coincide là où elle sont simultanément définies.
. Par prolongement analytique, on sait que les différentes
expresions obtenues coincide là où elle sont simultanément définies.
On utilisera donc si nécessaire différentes expressions pour le calcul des fonctions 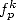 en
en 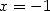 et
et 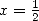 .
.
On déduit du calcul de 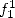 que
que
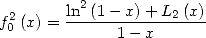 | (611) |
puis par intégration que
Enfin
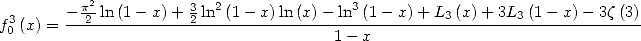 | (613) |
et ainsi
On en déduit que
Par un calcul de primitive, on a
ce qui donne pour  réel
réel
et
et enfin
13.3 Application au calcul de certaines séries
On utilise les résultats précédent avec des valeurs judicieusement choisies pour 
13.3.1 Avec 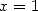
Les valeurs s’obtiennent plus facilement avec les fonctions Beta, par exemple
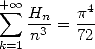 | (628) |
13.3.2 Avec 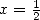
On obtient en prenant les valeurs des fonctions 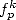 et
et 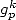 en
en 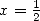
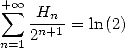 | (629) |
En combinant, on obtient
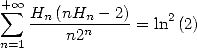 | (633) |
On peut obtenir alors
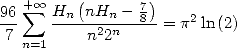 | (636) |
On peut combiner ces résultats et obtenir
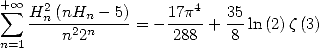 | (645) |
13.3.3 Avec 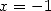
La convergence de la série ne pose pas de problème pour 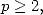 on obtient alors
on obtient alors
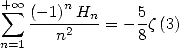 | (646) |
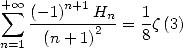 | (647) |
Pour 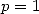 on trouve formellement
on trouve formellement
Ce qui donne
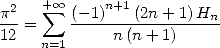 | (650) |
Ces égalité se justifient car les séries alternées converge et par avec un théorème du type Tauber, on conclue.
Les deux égalités suivantes sont obtenues formellement par Maple, elle se vérifient numériquement mais je n’arrive pas à les justifier
correctement.
ce qui donne en les soustrayant et avec 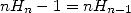
On a aussi
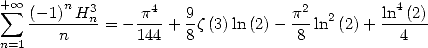 | (654) |
13.3.4 Avec 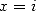
On obtient alors en considérant les parties réelles et imaginaires
La convergence est assurée en faisant 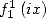 pour
pour 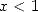 réel et par passage à la limite en
réel et par passage à la limite en 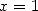 avec le lemme
d’Abel.
avec le lemme
d’Abel.
Avec 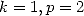 On obtient compte tenu de la valeur de
On obtient compte tenu de la valeur de 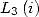 et de l’égalité de Landen en
et de l’égalité de Landen en 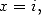
Or, il est prouvé dans [12] (calcul de 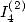 )
)
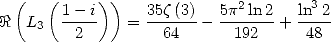 | (658) |
ce qui donne
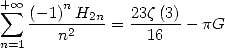 | (659) |
et permet d’obtenir avec 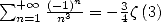
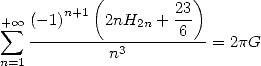 | (660) |
Avec  Les calculs sont un peu plus compliqué, on utilise cette fois ci l’égalité (658), puis la formule d’inversion pour le polylogarithme d’ordre
Les calculs sont un peu plus compliqué, on utilise cette fois ci l’égalité (658), puis la formule d’inversion pour le polylogarithme d’ordre
 qui donne
qui donne
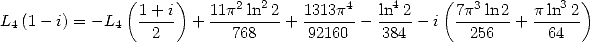 | (661) |
ainsi que
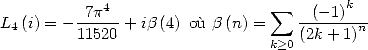 | (662) |
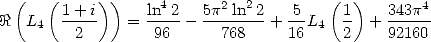 | (663) |
qui correspond au calcul de 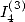 dans mon papier ”formules BBP”, on obtient
dans mon papier ”formules BBP”, on obtient
On applique les mêmes substitutions pour 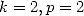 et
et 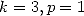 . On obtient alors en considérant la partie réelle (la partie
imaginaire ne donne rien d’utilisable)
. On obtient alors en considérant la partie réelle (la partie
imaginaire ne donne rien d’utilisable)
En combinant les différentes équations obtenues, on en déduit
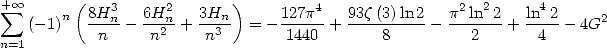 | (667) |
13.3.5 Avec 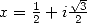
On utilise dans ce cas les résultats suivants.
Si on pose
(mgl signifie ”multiple Glaishers” et mcl signifie ”multiple Clausen”) alors
où 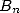 est le énième polynôme de Bernoulli.
est le énième polynôme de Bernoulli.
Puis la formule de duplication
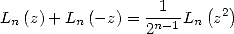 | (672) |
avec 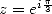 qui permet d’exprimer
qui permet d’exprimer 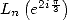 et
et 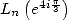 à l’aide de
à l’aide de 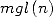 et
et 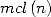 .
.
On obtient alors les résultats suivants :
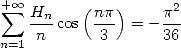 | (675) |
la convergence de cette série se justifie par sommation par paquets.
On obtient aussi (sous réserve de convergence, mais elle est au mieux si lente que c’est difficile à vérifier ! ! !)
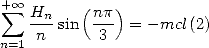 | (676) |
mais
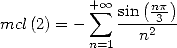 | (677) |
d’où
soit
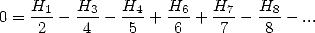 | (679) |
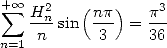 | (680) |
ce qui donne
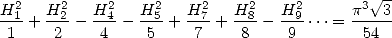 | (681) |
la convergence de cette série se justifie par sommation par paquets.
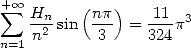 | (682) |
ce qui donne
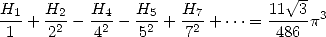 | (683) |
on a également
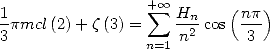 | (684) |
Avec 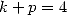 on obtient la belle formule suivante
on obtient la belle formule suivante
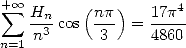 | (685) |
les autres font intervenir des 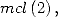
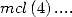
Par exemple
ce qui donne avec
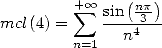 | (688) |
13.3.6 Avec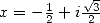
En utilisant l’égalité
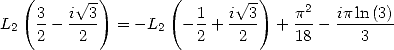 | (690) |
et sa conjuguée, on obtient
dont la convergence est assurée par paquets.
En combinant avec (675), on obtient
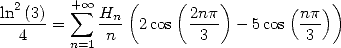 | (692) |
13.3.7 Avec 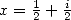
Pour 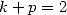 On obtient avec
On obtient avec 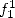 les deux formules suivantes qui sont remarquables
les deux formules suivantes qui sont remarquables
et avec 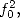 les deux égalités
les deux égalités
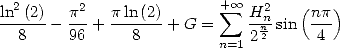 | (696) |
Avec les fonctions 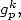 on a
on a
Avec 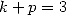 La fonction
La fonction 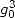 donne immédiatement
donne immédiatement
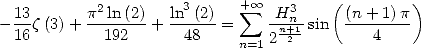 | (698) |
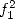 et
et 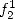 donnent
donnent
13.4 Généralisations
13.4.1 Sommes d’Euler
Si on définit 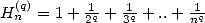 (somme partielle de
(somme partielle de 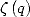 ), on a le théorème d’Euler.
), on a le théorème d’Euler.
Si 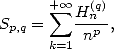 alors
alors 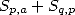 s’exprime à l’aide de
s’exprime à l’aide de 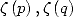 et
et 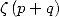
On a des relations avec les polylog : 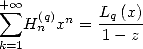 . En intégrant on a par exemple
. En intégrant on a par exemple
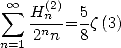 | (701) |
13.4.2 Une formule combinant Harmoniques et combinatoire
Voici une petite série que j’ai trouvée récemment en novembre 2001, mélangeant les combinaisons et les sommes harmoniques ! On peut peut-être trouver une preuve plus simple, quoique je la trouve assez élégante finalement.
D’accord, c’est un cas assez particulier, je ne sais pas si l’on peut trouver d’autres séries de ce type (et numériquement je n’en ai pas trouvé), mais cela vaut le coup de farfouiller un peu !
Preuve. Posons 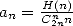 . Alors
. Alors
donc
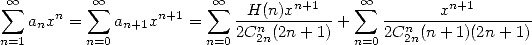 | (704) |
donc en particulier en 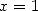 et en regroupant les deux séries contenant des
et en regroupant les deux séries contenant des 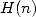 , on obtient
, on obtient
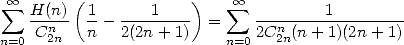 | (705) |
ce qui simplifie un peu le travail !
L’astuce 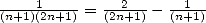 ne semble hélas pas utile car la série en
ne semble hélas pas utile car la série en 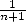 se révèle difficile à calculer il me semble... Passons
par un autre chemin.
se révèle difficile à calculer il me semble... Passons
par un autre chemin.
Notons ainsi que l’on a 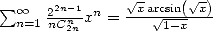 soit
soit 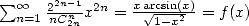 .
.
Donc
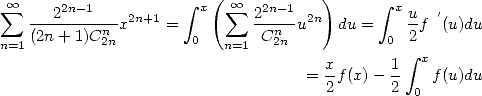
par intégration par parties. Donc puisque ![integral [V ~ ------ ] integral
0xua V~ r1cs-inu(2u)du = - 1- u2arcsin (u) x0 + 0xudu](../mathematiciens/huvent/hyperg2002x.gif) par intégration par parties, tout
simplement,
par intégration par parties, tout
simplement,
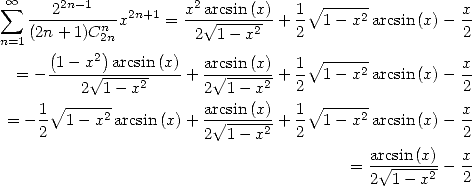
sur le rayon de convergence (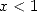 ).
).
Il reste à intégrer cette série correctement pour trouver un terme en 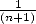 :
:
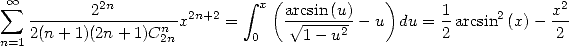 | (706) |
soit en ajoutant le terme pour 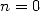 :
:
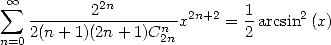 | (707) |
On utilise maintenant 705 pour obtenir
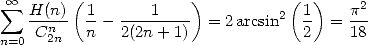 | (708) |
donc finalement
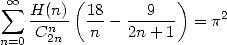 | (709) |
_
13.4.3 Une autre formule
On trouve aussi des formules avec des sommes harmoniques spéciales telles que la formule de Bradley :
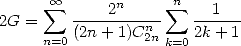 | (710) |
ou encore cette représentation de 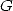 qui présente de troublantes ressemblanes avec la précédente !
qui présente de troublantes ressemblanes avec la précédente !
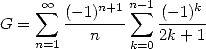 | (711) |
La preuve est disponible dans [10].
13.4.4 Harmoniques d’harmoniques !
D’après le Gradshteyn [9] (1.516), on peut obtenir immédiatement
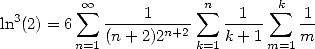 | (712) |
Retour à la page d'accueil