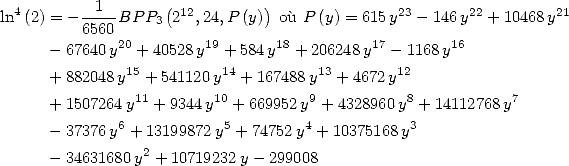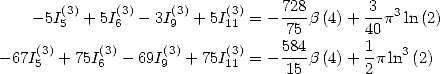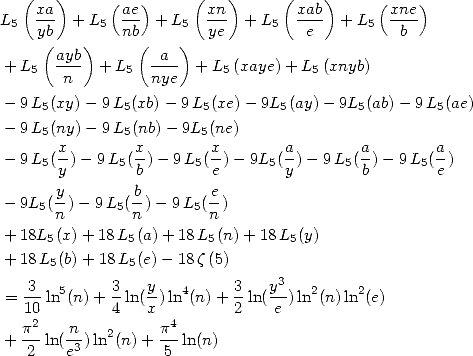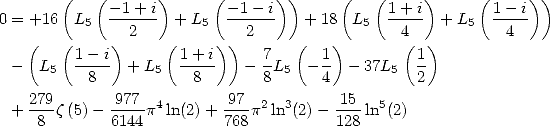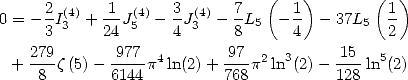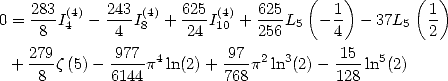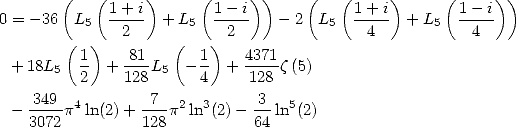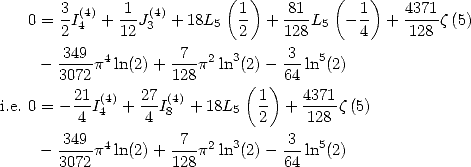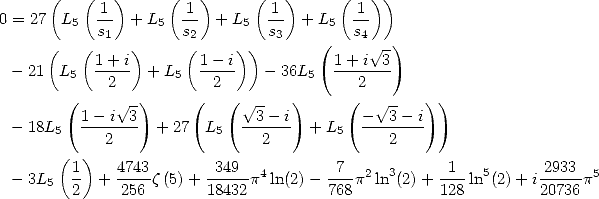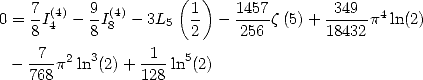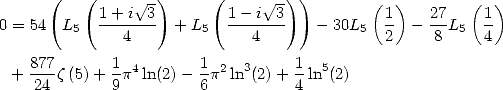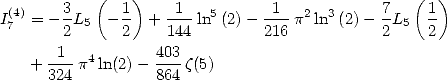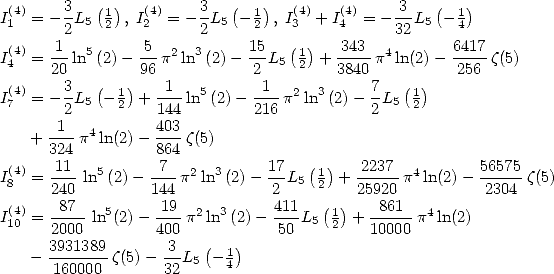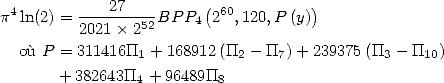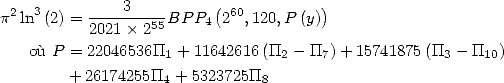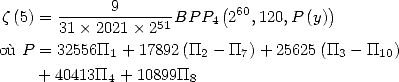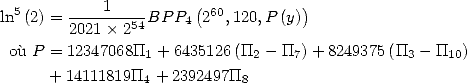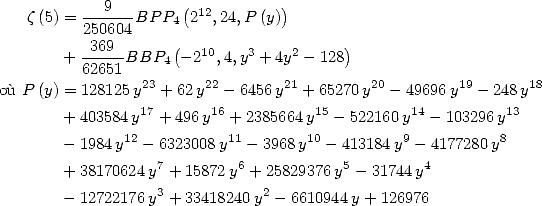|
|
|
|
|
6 Formules BBP en base 2 :  ,
, ,
, 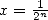 dans
dans 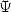
6.1 Les intégrales considérées
Dnas le souci constant de décomposer nos intégrales 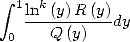 en intégrales plus simples à calculer, on s’intéresse aux intégrales
”primaires” suivantes :
en intégrales plus simples à calculer, on s’intéresse aux intégrales
”primaires” suivantes :
 | (83) |
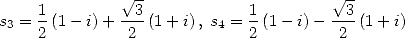 | (84) |
Dans [3], Broadhurst établi des relations entre différentes sommes de polylogarithmes. Cependant il ne semble pas envisager le lien avec les intégrales. On se propose de le faire. C’est pourquoi on introduit les intégrales suivantes :
Le lien entre les 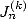 et les
et les 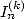 est le suivant :
est le suivant :
6.2 La méthode
Le calcul des intégrales 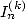 va fournir des combinaisons linéaires de constantes d’ordre
va fournir des combinaisons linéaires de constantes d’ordre 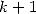 comme
comme 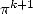 ou
ou 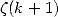 grâce à leurs
expressions sou la forme de polylogarithmes d’ordre
grâce à leurs
expressions sou la forme de polylogarithmes d’ordre 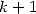 . Mais dautre part, on peut obtenir des formules BBP avec les
. Mais dautre part, on peut obtenir des formules BBP avec les 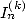 en utilisant
ce que Gery Huvent appelle les tableaux de dénomination et qui ne sont que les expressions des
en utilisant
ce que Gery Huvent appelle les tableaux de dénomination et qui ne sont que les expressions des 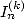 sous la forme d’intégrales
sous la forme d’intégrales 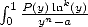 dont on a vu l’expression directe sous forme d’une série BBP avec la formule (69). Il reste à obtenir des séries BBP pour les constantes
précises qui nous intéressent, ce qui revient à utiliser une certaine combinaison linéaire des
dont on a vu l’expression directe sous forme d’une série BBP avec la formule (69). Il reste à obtenir des séries BBP pour les constantes
précises qui nous intéressent, ce qui revient à utiliser une certaine combinaison linéaire des 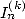 . Pour ceci, on introduit de
manière générale la forme linéaire
. Pour ceci, on introduit de
manière générale la forme linéaire 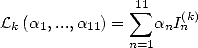 . Puis l’on impose des relations entre les
. Puis l’on impose des relations entre les 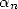 pour annuler
les coefficients de vant les constantes qui ne nous intéressent pas. On obtient alors une série BBP pour ce qui reste,
pour annuler
les coefficients de vant les constantes qui ne nous intéressent pas. On obtient alors une série BBP pour ce qui reste, 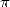 ou
ou 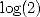 ou bien d’autres choses encore ! Voici les tableaux des dénominateurs. La méthode est ensuite détaillée sur un
exemple.
ou bien d’autres choses encore ! Voici les tableaux des dénominateurs. La méthode est ensuite détaillée sur un
exemple.
où 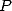 est un polynôme à coefficients entiers qui dépend à la fois de
est un polynôme à coefficients entiers qui dépend à la fois de 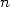 et du dénominateur choisi.
et du dénominateur choisi.
6.3 Formules pour 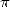 ,
, 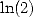 ,
, 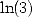 et
et 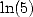
Dans le cas où 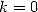 , on obtient, par un calcul des intégrales
, on obtient, par un calcul des intégrales
6.3.1 Application aux formules BBP pour 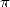
Afin d’obtenir des formules pour 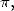 on impose les relations suivantes :
on impose les relations suivantes :
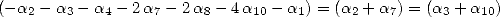
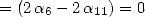 .
.
On a alors
Pour avoir des formules BBP ayant peu de termes, on peut dans un premier temps imposer 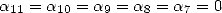 , ce qui
donne
, ce qui
donne
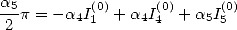 | (113) |
On consulte alors la table des dénominateurs. Pour simplifier une somme faisant intervenir 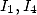 et
et 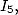 on écrit chaque intégrale sous la
forme
on écrit chaque intégrale sous la
forme 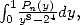
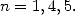 Ainsi
Ainsi
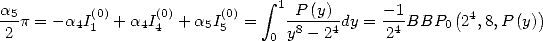 | (114) |
où 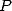 est un polynôme dont les coefficients dépendent de
est un polynôme dont les coefficients dépendent de 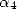 et
et 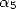 . Si l’on impose
. Si l’on impose 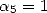 et
et 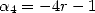 on obtient la formule
d’Adamchik-Wagon (cf [6] )
on obtient la formule
d’Adamchik-Wagon (cf [6] )
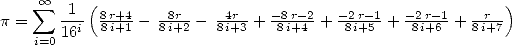 | (Adamchik-Wagon) |
Le choix de 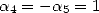 donne la formule de Plouffe (61). On peut maintenant chercher un dénominateur en
donne la formule de Plouffe (61). On peut maintenant chercher un dénominateur en 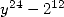 . On reprend
alors la formule (111) et on impose simplement
. On reprend
alors la formule (111) et on impose simplement 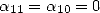 .
.
On choisit les autres coefficients de manière à annuler le plus de coefficients de 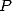 (en imposant
(en imposant 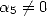 ).
).
Le meilleur choix semble être
![[ai] = (a1,...,a11) = (0,- 1,0,1,1,0,1,-1,-1,0,0)](../mathematiciens/huvent/hyperg367x.gif) qui donne
qui donne
On peut aussi chercher un dénominateur en 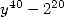 en imposant
en imposant 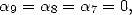 le meilleur choix semble être
le meilleur choix semble être
![[a ] = (a ,...,a ) = (0,0,0,0,-2,1,0,0,0,0,1)
i 1 11](../mathematiciens/huvent/hyperg371x.gif) qui donne
qui donne
En fait il s’avère que dans la dernière formule 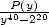 peut se simplifier en
peut se simplifier en 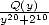 , ce qui donne la formule alternée :
, ce qui donne la formule alternée :
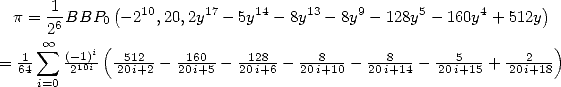 | (Bellard) (119) |
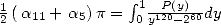 , il
reste à choisir judicieusement les
, il
reste à choisir judicieusement les 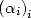 . Le choix qui conduit à une formule ayant le moins de termes possible semble
être
. Le choix qui conduit à une formule ayant le moins de termes possible semble
être
![[ai] = (a1,...,a11) = (0,0,0,0,0,1,0,0,- 2,0,1)](../mathematiciens/huvent/hyperg378x.gif) et donne
et donne
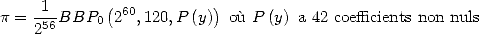 | (120) |
On peut expliciter 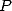 en écrivant que
en écrivant que
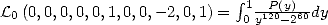 .
.
Pour finir, le choix de ![[a] = (0,0,0,0,0,1,0,0,-2,0,1)](../mathematiciens/huvent/hyperg382x.gif) conduit à
conduit à
Et ![[a] = (0,0,0,0,2,0,0,0,-2,0,0)](../mathematiciens/huvent/hyperg384x.gif) donne
donne
6.3.2 Formules BBP pour  et
et 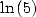
On peut appliquer ces mêmes méthodes pour obtenir des formules 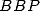 pour
pour 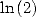 ,
, 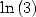 et
et 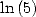 .
.
6.4 Cas des polylogarithmes d’ordre  : Formules d’ordre 2
: Formules d’ordre 2
On peut remarquer qu’à l’ordre 1, c’est-à-dire pour des formules BBP donnant 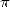 ou
ou 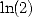 par exemple, on avait affaire à des intégrales de
fractions rationnelles. Si l’on veut obtenir maintenant des séries de type BBP donnant
par exemple, on avait affaire à des intégrales de
fractions rationnelles. Si l’on veut obtenir maintenant des séries de type BBP donnant 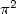 ou
ou 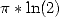 ou
ou 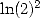 , il va falloir introduire
un logarithme au numérateur de l’intégrale. Plus précisément, pour une formule BBP d’ordre
, il va falloir introduire
un logarithme au numérateur de l’intégrale. Plus précisément, pour une formule BBP d’ordre 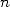 , il faudra considérer des
intégrales du type
, il faudra considérer des
intégrales du type 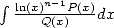 . Ceci est dû au fait que l’on obtient alors des combinaisons de polylogarithmes d’ordre
. Ceci est dû au fait que l’on obtient alors des combinaisons de polylogarithmes d’ordre
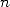 .
.
C’est ce que réalise encore une fois Gery Huvent [12], tout en notant également que les premières séries avaient été obtenues par Plouffe et
que Broadhurst [3] en a également fourni. L’intérêt de l’ordre 2 est de pouvoir fournir des séries BBP pour une constante célèbre qui est la
constante de Catalan définie par 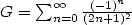 . Ceci montre, si on n’en était pas convaincu, que la constante de Catalan est
”homogène” à un ordre 2, c’est-à-dire qu’elle est sans aucun doute de même nature que
. Ceci montre, si on n’en était pas convaincu, que la constante de Catalan est
”homogène” à un ordre 2, c’est-à-dire qu’elle est sans aucun doute de même nature que 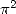 ou
ou 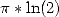 concernant la répartition de ses
digits en base 2 ou 16.
concernant la répartition de ses
digits en base 2 ou 16.
6.4.1 Les expressions classiques : 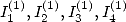 et
et 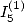
Un résultat classique d’Euler est
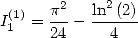 | (123) |
Ce qui permet d’écrire que
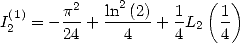 | (124) |
L’équation de Kummer pour le polylogarithme d’ordre  s’écrit (cf [4])
s’écrit (cf [4])
La formule d’inversion est
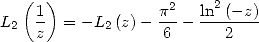 | (Formule d’inversion) |
et enfin la formule de duplication dans le cas général :
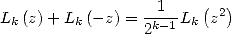 | (Formule de duplication) |
En appliquant l’équation de Kummer pour 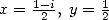 puis
puis 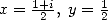 , on obtient deux égalités qui additionnées
donnent
, on obtient deux égalités qui additionnées
donnent
En utilisant formule la d’inversion pour 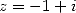 et
et 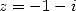 et la formule de duplication , on obtient
et la formule de duplication , on obtient
Par duplication, on a aussi
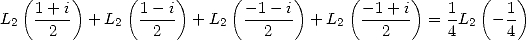 | (128) |
On en déduit
De la même manière, l’équation de Kummer pour 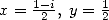 puis
puis 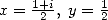 , donnent deux égalités qui soustraites donnent
une nouvelle égalité. En utilisant ensuite la formule d’inversion pour
, donnent deux égalités qui soustraites donnent
une nouvelle égalité. En utilisant ensuite la formule d’inversion pour 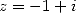 et
et 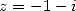 et la formule de duplication pour
et la formule de duplication pour 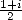 et
et
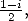 on obtient
on obtient
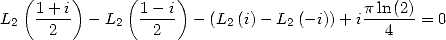 | (131) |
Mais 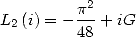 où
où 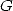 est la constante de Catalan. Ainsi
est la constante de Catalan. Ainsi
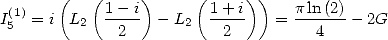 | (132) |
6.4.2 Calcul de 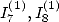 et
et 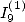
Proposition 2 On a
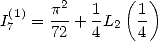 | (133) |
Preuve. L’équation de Kummer avec 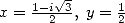 donne l’égalité
donne l’égalité
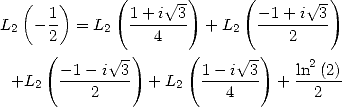
ce qui donne immédiatement le résultat cherché car
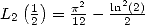 ,
, 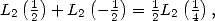
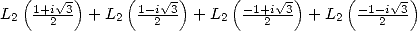
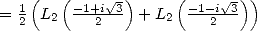 par la formule de duplication et la formule de Kummer pour
par la formule de duplication et la formule de Kummer pour 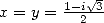 donne
donne
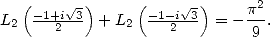 _
_
Proposition 3 On a
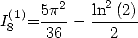 | (134) |
et
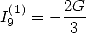 | (135) |
Preuve. L’équation de Kummer pour 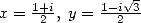 donne, compte tenu de
donne, compte tenu de
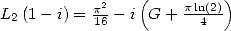

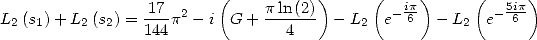 | (136) |
de même, l’équation de Kummer pour 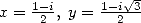 donne
donne
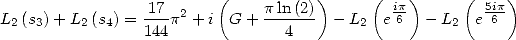 | (137) |
A l’aide de la formule d’inversion
Ce qui permet de conclure que
et
Il reste donc à calculer la dernière somme de polylogarithmes. Mais on a gagné en simplicité car ces polylogarithmes font intervenir des
racines de l’unité .
On utilise alors la formule de multiplication
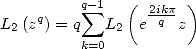 | (Formule de multiplication) |
qui donne avec 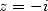 et
et 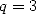
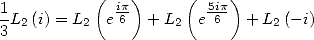 | (144) |
puis avec 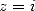 et
et 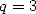
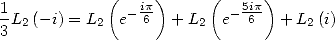 | (145) |
et permet facilement de conclure. _
6.4.3 Calcul de 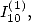 relation entre
relation entre 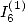 et
et 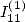
L’équation de Kummer pour 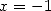 et
et 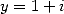 et pour
et pour 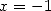 et
et 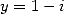 donne deux égalités qui additionnées
fournissent
donne deux égalités qui additionnées
fournissent
Ce qui se traduit par
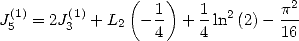 | (147) |
et permet d’affirmer que
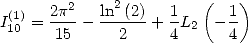 | (148) |
Si, au lieu de les additionner, on soustrait ces égalités, on obtient
ce qui donne
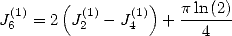 | (150) |
i.e.
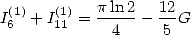 | (151) |
6.4.4 Application à la détermination de formules BBP
On considère maintenant la forme linéaire 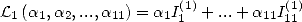 . Compte tenu des égalités (123), (124), (129), (130),
(132), (133), (134), (135) et (148), on a
. Compte tenu des égalités (123), (124), (129), (130),
(132), (133), (134), (135) et (148), on a
Formules pour 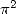 Afin d’obtenir des formules BBP pour
Afin d’obtenir des formules BBP pour 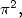 on impose les relations suivantes :
on impose les relations suivantes :
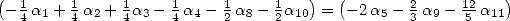
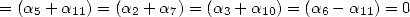 pour obtenir l’égalité
pour obtenir l’égalité
Il suffit maintenant de particulariser les variables pour obtenir des formules simples.
Quelques formules simples déjà connues pour 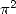
On obtient ces formules en choisissant les intégrales qui donnent un dénominateur de plus bas degré dans le tableau de
correspondance.
Détaillons une dernière fois un exemple :
Afin d’obtenir un dénominateur de la forme 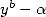 de plus bas degré (en l’occurrence
de plus bas degré (en l’occurrence 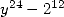 ), on choisit
), on choisit 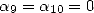 de manière à
faire disparaître
de manière à
faire disparaître 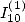 et
et 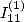 . On a alors
. On a alors
Cette égalité permet de donner la formule générale à 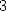 paramètres
paramètres
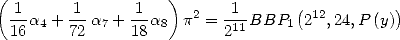 | (160) |
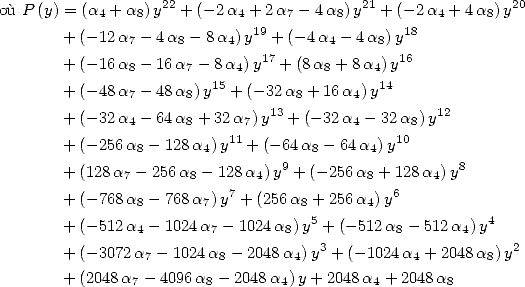
Afin de ne pas alourdir l’exposé seules les formules à paramètres qui correspondent au dénominateur en 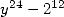 seront données. Il en
existe qui sont associées à d’autres dénominateurs (par exemple
seront données. Il en
existe qui sont associées à d’autres dénominateurs (par exemple 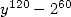 ).
).
Revenons à l’égalité (159), si l’on choisit de poser 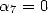 et
et 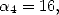 cette égalité devient
cette égalité devient
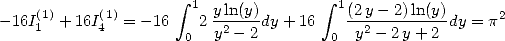 | (161) |
On peut traduire cette égalité sous forme de somme de formule BBP.
On peut ramener cette intégrale à un dénominateur de la forme 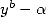 à l’aide du tableau de correspondance pour
obtenir
à l’aide du tableau de correspondance pour
obtenir
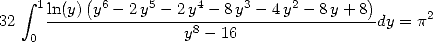 | (163) |
qui donne l’égalité suivante
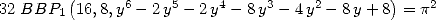 | (164) |
ou
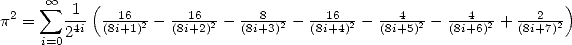 | (165) |
Cette égalité est déjà mentionnée par Plouffe dans [1]
Le choix de 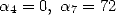 donne
donne
ce qui donne la formule suivante due à Plouffe :
Quelques formules simples et nouvelles
Une autre solution consiste à garder les intégrales qui fournissent des dénominateurs de la forme 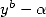 de degré élévé mais d’ajuster les
paramètres de manière à avoir beaucoup de coefficients nuls dans les formules BBP.
de degré élévé mais d’ajuster les
paramètres de manière à avoir beaucoup de coefficients nuls dans les formules BBP.
De bon choix semblent être les suivants :
![[ai] = (a1,...,a11) = (1,1,0,0,0,0,- 1,0,0,0,0)](../mathematiciens/huvent/hyperg504x.gif) qui donne la formule à
qui donne la formule à 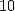 termes
termes
Le polynôme 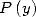 n’ayant que des puissances impaires, cette formule peut se simplifier pour donner
n’ayant que des puissances impaires, cette formule peut se simplifier pour donner
![[ai] = (2,1,0,1,0,0,- 1,- 1,0,0,0)](../mathematiciens/huvent/hyperg509x.gif) qui donne la formule à
qui donne la formule à 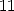 termes
termes
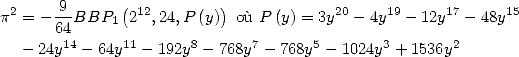
![[a] = (- 2,-1,-1,- 2,0,0,1,0,0,1,0)
i](../mathematiciens/huvent/hyperg512x.gif) qui donne la formule
qui donne la formule 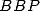 à
à 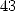 termes (remarquer le
termes (remarquer le 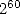 ) :
) :
Si l’on s’intéresse aux formules ayant le moins de termes, citons que d’autres formules à 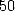 termes (
termes (![[ai] = (- 1,- 1,0,0,0,0,1,0,0,0,0)](../mathematiciens/huvent/hyperg518x.gif) ) et à
) et à 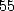 termes (
termes (![[ai] = (- 2,-1,0,-1,0,0,1,1,0,0,0)](../mathematiciens/huvent/hyperg520x.gif) ) existent.
) existent.
On peut également chercher des séries alternées, par exemple
![[ai] = (0,0,0,-2,0,0,0,,0,0,0)](../mathematiciens/huvent/hyperg521x.gif) donne
donne
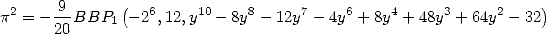 | (Huvent) |
Remarque
Les égalités intégrales permettent aussi d’écrire de différentes façons 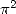 comme somme de formule BBP.
comme somme de formule BBP.
Par exemple, le résultat (Huvent) (![[ai] = (-1,- 1,0,0,0,0,1,0,0,0,0)](../mathematiciens/huvent/hyperg524x.gif) ) donne l’égalité intégrale
) donne l’égalité intégrale
Ce qui peut s’écrire
Formules pour les constantes 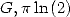 et
et 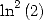 Pour
Pour 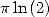
La même méthode conduit à la formule générale pour 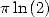 (lorsque l’on impose un dénominateur en
(lorsque l’on impose un dénominateur en 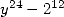 )
)
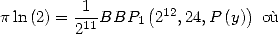 | (Huvent) |
En ajustant les coefficients 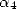 et
et 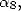 on dispose de formules ayant
on dispose de formules ayant 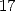 termes qui sont de la forme
termes qui sont de la forme
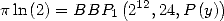
Une des plus simples semble être ![[ai] = (2,- 6,0,4,1,0,6,- 6,-3,0,0)](../mathematiciens/huvent/hyperg538x.gif)
Une autre formule à 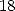 termes est obtenue pour
termes est obtenue pour ![[a] = (0,0,0,0,1,0,0,0,-3,0,0)
i](../mathematiciens/huvent/hyperg541x.gif)
Pour terminer ![[ai] = (0,0,0,0,4,1,0,0,0,0,1)](../mathematiciens/huvent/hyperg543x.gif) donne
donne
Pour la constante de Catalan 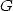
De même, en imposant un dénominateur en 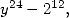 on obtient
on obtient
Le cas le plus intéressant est obtenue quand tous les 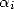 sont nuls excepté
sont nuls excepté 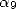 que l’on prend égal à
que l’on prend égal à 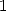 . On obtient
ainsi
. On obtient
ainsi
L’intérêt de cette formule réside dans les coefficients de 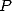 qui sont tous des puissances de
qui sont tous des puissances de  .
.
Le choix de ![[ai] = (1,- 3,0,2,0,0,3,-3,1,0,0)](../mathematiciens/huvent/hyperg554x.gif) permet d’écrire
permet d’écrire
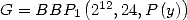 où
où 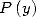 a
a 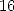 coefficients non nuls.
coefficients non nuls.
Pour finir ![[a ] = (0,0,0,0,- 1,1,0,0,-1,0,1)
i](../mathematiciens/huvent/hyperg558x.gif) donne
donne 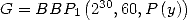 où
où 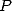 a
a 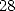 coefficients non nuls.
coefficients non nuls.
Remarque 4 Il semble que j’avais été le premier à avoir découvert expérimentalement une vraie formule 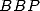 pour
pour 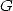 (Mai
2000) sans toutefois fournir de preuve. Le problème se discute entre moi et David Broadhurst sans doute, mais ce n’est pas très
important...
(Mai
2000) sans toutefois fournir de preuve. Le problème se discute entre moi et David Broadhurst sans doute, mais ce n’est pas très
important...
Pour 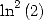
On obtient
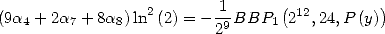 | (173) |
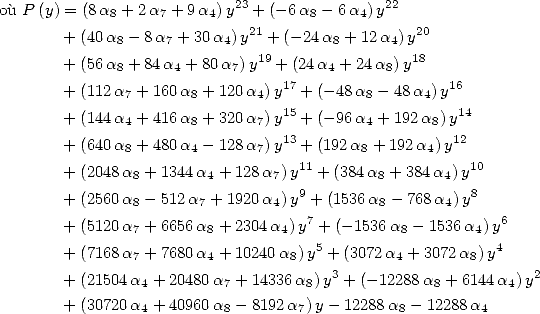
Le cas le plus simple est donné par ![[ai] = (- 4,- 3,0,0,0,0,3,0,0,0,0)](../mathematiciens/huvent/hyperg567x.gif) qui conduit à
qui conduit à
Le choix de ![[ai] = (- 42,-21,-20,- 40,0,0,21,0,0,20,0)](../mathematiciens/huvent/hyperg569x.gif) conduit à
conduit à 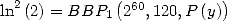 où
où 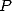 a
a 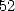 coefficients non
nuls.
coefficients non
nuls.
6.4.5 Quelques formules composites
Dans la détermination de formules BBP, on a systématiquement annulé les coefficients de 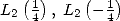 et
et 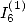 . Si l’on décide alors de
garder ces termes, on obtient parmi les formules possibles, les résultats suivants :
. Si l’on décide alors de
garder ces termes, on obtient parmi les formules possibles, les résultats suivants :
![[a] = (1,1,0,0,0,0,2,0,0,0,0)](../mathematiciens/huvent/hyperg575x.gif) donne
donne
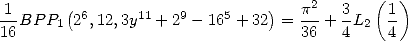 | (174) |
qui se simplifie en
Cette formule est équivalente à la formule (167). Si on applique cette idée pour la constante de Catalan, on obtient avec
![[a] = (0,0,0,0,0,-1,0,0,1,0,0)](../mathematiciens/huvent/hyperg578x.gif) l’égalité
l’égalité
Ce qui sous forme de séries donne les deux égalités suivantes :
La même idée conduit, avec ![[a] = (0,0,0,0,-4,8,0,0,- 12,0,0)](../mathematiciens/huvent/hyperg581x.gif) à
à
et avec ![[a] = (4,8,0,0,- 4,4,12,0,0,0,0)](../mathematiciens/huvent/hyperg583x.gif) à
à
Ce genre de formule n’a pas systématiquement été recherché.
6.5 Cas des polylogarithmes d’ordre 3
L’ordre 3 introduit bien entendu des formules donnant 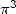 et autres
et autres 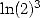 mais surtout la célèbre constante
mais surtout la célèbre constante 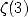 démontrée irrationnelle
par Apéry en 1978 [14] au moyen d’un développement en fraction continue d’une formule factorielle dont on parle un peu plus loin
justement.
démontrée irrationnelle
par Apéry en 1978 [14] au moyen d’un développement en fraction continue d’une formule factorielle dont on parle un peu plus loin
justement.
Cette constante reste toutefois mystérieuse, et les formules BBP montrent intuitivement que cette constante n’est sans doute pas très différente du point de vue de l’ordonnancement de ses décimales et donc de sa complexité.
L’équation de Kummer pour le trilogarithme s’écrit
et la formule d’inversion
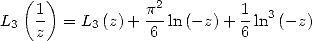 | (181) |
Un résultat classique permet d’affirmer que
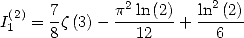 | (182) |
et par définition
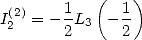 | (183) |
6.5.1 Calcul de 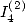
L’équation de Landen pour le trilogarithme (cf [4] ) est
Appliquée à 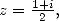 on obtient (avec
on obtient (avec 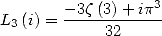 )
)
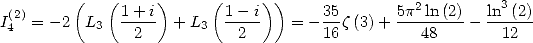 | (185) |
résultat implicitement contenu dans [3].
On en déduit par la formule de duplication que
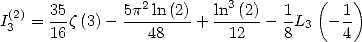 | (186) |
6.5.2 Calcul de 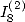
Comme pour le calcul de 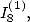 on utilise l’équation de Kummer avec
on utilise l’équation de Kummer avec 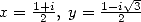 puis avec
puis avec 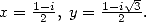 On additionne
alors les deux équations obtenues. On simplifie ces équations à l’aide de la valeur de
On additionne
alors les deux équations obtenues. On simplifie ces équations à l’aide de la valeur de 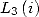 et de l’égalité
et de l’égalité 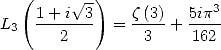 .
Ceci permet d’affirmer que
.
Ceci permet d’affirmer que
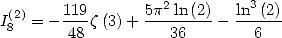 | (187) |
6.5.3 Relation entre 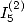 et
et 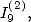 valeur de
valeur de 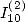
On reprend les deux premières équations du calcul de 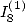 que l’on soustrait cette fois ci. On utilise ensuite la formule d’inversion avec
que l’on soustrait cette fois ci. On utilise ensuite la formule d’inversion avec
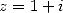 et
et 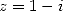 de manière à faire apparaître le terme
de manière à faire apparaître le terme 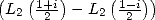 . Enfin une dernière application de la formule
d’inversion avec
. Enfin une dernière application de la formule
d’inversion avec 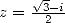 et avec
et avec 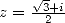 conduit à
conduit à
Ce qui prouve que
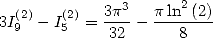 | (189) |
Si l’on utilise l’équation de Kummer avec 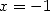 et
et 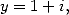 puis avec
puis avec 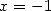 et
et 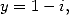 on obtient deux égalités que
l’on soustrait. On simplifie le résultat obtenu avec la formule d’inversion appliquée à
on obtient deux égalités que
l’on soustrait. On simplifie le résultat obtenu avec la formule d’inversion appliquée à 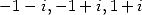 et
et 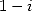 pour
obtenir
pour
obtenir
Cette égalité se traduit à l’aide des intégrales par
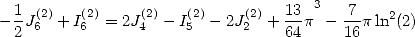 | (191) |
et donne la relation
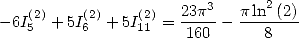 | (192) |
Si, au lieu de soustraire les égalités obtenues précédemment, on les additionne, on obtient :
ce qui donne
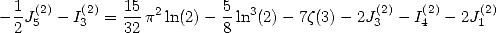 | (194) |
et fournit
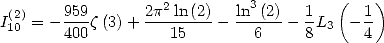 | (195) |
6.5.4 Calcul de 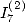
Comme pour le calcul de 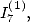 l’équation de Kummer pour le polylogarithme d’ordre
l’équation de Kummer pour le polylogarithme d’ordre 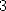 avec
avec 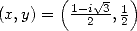 , puis la formule
d’inversion avec
, puis la formule
d’inversion avec 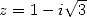 conduit immédiatement à
conduit immédiatement à
6.5.5 Application à la détermination de formules BBP
Considérons maintenant la forme linéaire 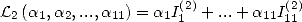 . Alors les résultats précédents permettent d’affirmer
que
. Alors les résultats précédents permettent d’affirmer
que
Formules pour 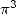 Si l’on cherche des formules pour
Si l’on cherche des formules pour 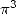 on annule les coefficients des constantes
on annule les coefficients des constantes
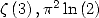 ... pour obtenir
... pour obtenir
On ne peut pas choisir 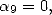 ce qui impose d’utiliser un dénominateur en
ce qui impose d’utiliser un dénominateur en  pour les formules BBP donnant
pour les formules BBP donnant 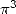 . En toute
généralité, on obtient ainsi une formule BPP pour
. En toute
généralité, on obtient ainsi une formule BPP pour 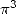 ayant deux paramètres (
ayant deux paramètres (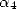 et
et 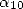 ), formule que le lecteur pourra établir. La
formule la plus simple est alors obtenue pour
), formule que le lecteur pourra établir. La
formule la plus simple est alors obtenue pour ![[a ] = (0,0,0,0,5,-5,0,0,3,0,- 5)
i](../mathematiciens/huvent/hyperg646x.gif) et a
et a 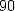 termes. Afin de l’écrire, on introduit les
polynômes
termes. Afin de l’écrire, on introduit les
polynômes 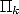 définies par
définies par 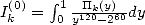 , par exemple
, par exemple 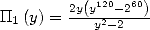 .
.
On a alors
Cette égalité peut s’écrire autrement.
En effet 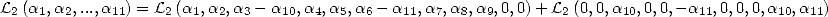
Mais 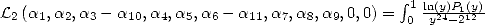 et
et
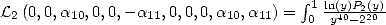 où
où 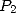 a
a  coefficients non nuls en général, et seulement
coefficients non nuls en général, et seulement 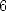 si
si 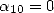 ou
ou
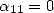 ou
ou 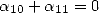 .
.
Si l’on applique cette remarque ici, on a
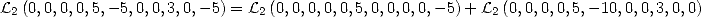 ce qui donne
ce qui donne
Cette formule peut aussi s’écrire
Formules pour 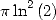 Pour obtenir une formule BBP simple pour
Pour obtenir une formule BBP simple pour 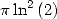 , on applique la même idée que pour
, on applique la même idée que pour 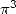 (le problème s’avère être le même, il faut
utiliser
(le problème s’avère être le même, il faut
utiliser 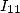 ce qui donne un dénominateur en
ce qui donne un dénominateur en 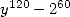 et donne une expression à deux paramètres)
et donne une expression à deux paramètres)
On obtient ainsi avec ![[ai] = (0,0,0,0,67,-75,0,0,69,0,- 75)](../mathematiciens/huvent/hyperg669x.gif)
Cette formule peut aussi s’écrire
Comparer avec celles obtenues pour 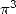 .
.
Formules pour 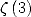 Pour
Pour 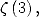 on obtient, si l’on cherche un dénominateur en
on obtient, si l’on cherche un dénominateur en 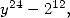
Ce qui donne la formule générale
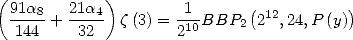 | (Huvent) |
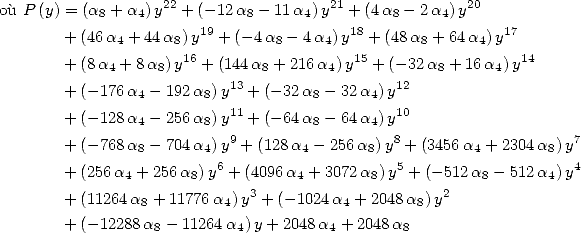
La formule BPP la plus simple est obtenue pour
![[a] = (-3,- 1,0,- 2,0,0,1,2,0,0,0)](../mathematiciens/huvent/hyperg679x.gif)
On peut aussi utiliser la remarque suivante :
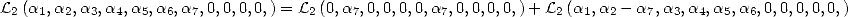
Mais 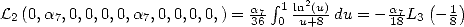 et
et
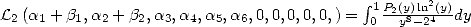
Si on impose alors 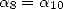 dans (203), on a
dans (203), on a 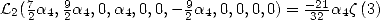
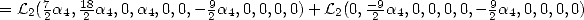 ce qui donne
ce qui donne
Enfin la formule la plus simple pour un dénominateur en 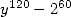 est obtenue avec
est obtenue avec
![[ai] = (8,4,5,9,0,0,- 4,1,0,- 5,0)](../mathematiciens/huvent/hyperg689x.gif) et contient
et contient 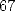 termes.
termes.
Remarque 5 De même ici, j’avais été je pense le premier à proposer une formule pour 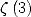 dont la démonstration, bien moins
simple mais sur le même modèle, était tout de même achevée en juin 2000 avec l’aide de Raymond Manzoni [5].
dont la démonstration, bien moins
simple mais sur le même modèle, était tout de même achevée en juin 2000 avec l’aide de Raymond Manzoni [5].
Formules pour 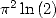 On obtient la formule générale suivante
On obtient la formule générale suivante
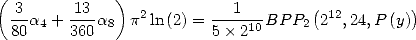 | (Huvent) |
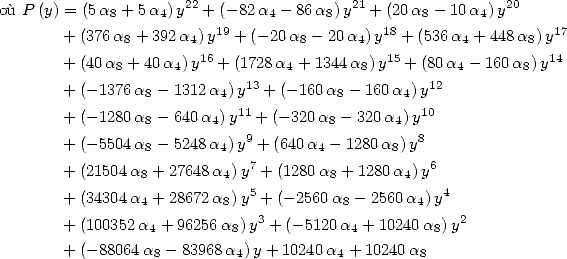
Avec ![[ai] = (-8,- 3,0,- 5,0,0,3,5,0,0,0)](../mathematiciens/huvent/hyperg695x.gif) , on a la formule à
, on a la formule à 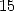 termes
termes
Cette relation est remarquable, en effet l’égalité (204) est obtenue pour ![[ai] = (- 3,-1,0,-2,0,0,1,2,0,0,0)](../mathematiciens/huvent/hyperg698x.gif) .
.
Cela conduit à poser
Alors
Enfin la formule la plus simple avec un dénominateur en 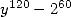 est obtenue avec
est obtenue avec
![[ai] = (42,21,25,46,0,0,- 21,4,0,-25,0)](../mathematiciens/huvent/hyperg704x.gif) et comporte
et comporte 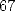 termes.
termes.
Formules pour 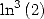 On a la formule générale
On a la formule générale
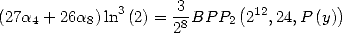 | (Huvent) |
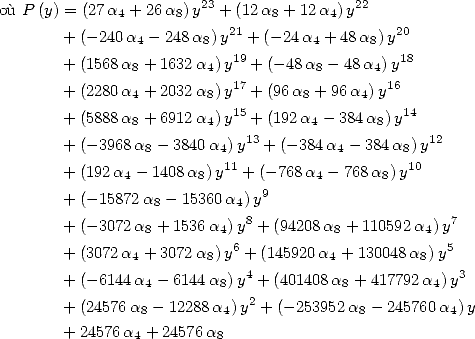
et la formule la plus simple est obtenue pour
![[ai] = (- 22,-9,0,-12,0,0,9,12,0,0,0)](../mathematiciens/huvent/hyperg709x.gif)
Et celle ayant un dénominateur en 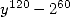 est donnée par
est donnée par
![[ai] = (- 202,-99,-100,- 200,0,0,99,0,0,100,0)](../mathematiciens/huvent/hyperg712x.gif)
6.6 Cas des polylogarithmes d’ordre 4
6.6.1 Les relations
Pour les polylogarithmes d’ordre 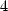 et
et 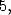 on ne dispose plus que d’un seul outil, à savoir l’équation de Kummer. Elle s’écrit, avec
on ne dispose plus que d’un seul outil, à savoir l’équation de Kummer. Elle s’écrit, avec
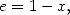
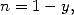
et la formule d’inversion
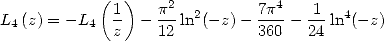 | (214) |
On applique alors la méthode suivante :
- Utilisation de la formule de Kummer en un couple 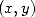 particulier
particulier
- Elimination des polylogarithmes d’argument de module supérieur à 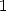 par la formule d’inversion
par la formule d’inversion
- Simplifications éventuelles à l’aide de la formule de duplication ou des valeurs de 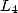 en
en 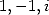 et
et 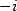 .
.
- Avec
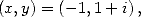 on obtient
on obtient
Ce qui se traduit avec les intégrales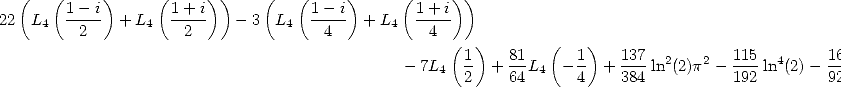
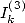 et
et 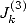 par
par
- Avec
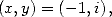 on obtient
on obtient
On obtient une seconde égalité par conjugaison (ou avec
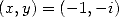 ). On additionne, ou soustrait les deux égalités obtenues et
en remplaçant
). On additionne, ou soustrait les deux égalités obtenues et
en remplaçant 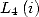 par
par 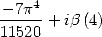 où
où 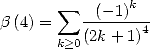 , cela fournit
, cela fournit
et
- Avec
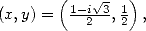 on obtient
on obtient
On utilise alors la formule de multiplication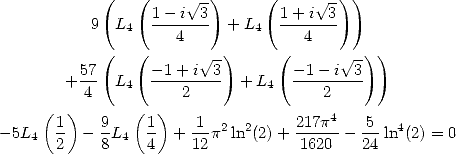
(221)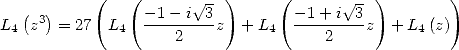
(222) qui avec
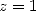 permet d’affirmer que
permet d’affirmer que
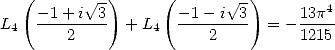
(223) et que
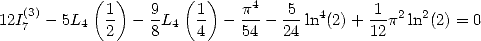
(224) - Enfin, avec
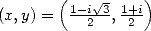 , on obtient
, on obtient
En considérant la partie réelle et la partie imaginaire de cette expression, on a respectivement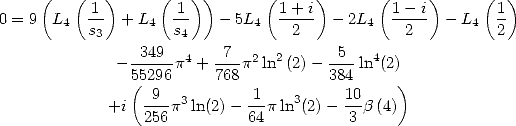
(225)
6.6.2 Application à la détermination de formules BBP
On considère maintenant la forme linéaire 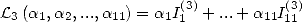 . Alors les résultats précédents fournissent
. Alors les résultats précédents fournissent
6.6.3 Formules pour 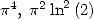 et
et 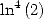
Pour 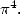 La formule la plus simple (et la seule associée à un dénominateur en
La formule la plus simple (et la seule associée à un dénominateur en 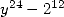 ) est obtenue pour
) est obtenue pour ![[ai] = (37,9,0,26,0,0,-9,- 27,0,0,0)](../mathematiciens/huvent/hyperg753x.gif) et donne
et donne
Il existe une formule à deux paramètre ayant un dénominateur en 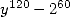 , la plus simple est donnée par
, la plus simple est donnée par
![[ai] = (34,18,25,41,0,0,- 18,18,0,-25,0)](../mathematiciens/huvent/hyperg756x.gif)
Pour 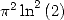 La formule la plus simple est obtenue pour
La formule la plus simple est obtenue pour
![[ai] = (- 10381,-3303,0,- 6836,0,0,3303,6957,0,0,0)](../mathematiciens/huvent/hyperg758x.gif) et donne
et donne
Le cas de 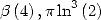 et
et 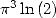 Il n’est pas possible de déterminer des formules
Il n’est pas possible de déterminer des formules 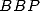 pour ces constantes, on ne trouve que deux relations indépendantes qui
sont :
pour ces constantes, on ne trouve que deux relations indépendantes qui
sont :
Cela montre qu’il suffit de trouver une formule 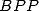 pour l’une des trois constantes
pour l’une des trois constantes 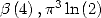 et
et 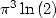 pour en déduire une
pour les deux autres.
pour en déduire une
pour les deux autres.
6.7 Cas des polylogarithmes d’ordre 5
6.7.1 Les relations
Broadhurst dans [3] exhibe des relations entre les intégrales 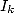 et
et 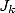 à l’aide de l’équation de Kummer (relations
à l’aide de l’équation de Kummer (relations 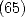 à
à
 . Puis découvre deux égalités de façon numérique (relations
. Puis découvre deux égalités de façon numérique (relations 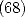 et
et 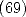 ). Il prouve alors la relation
). Il prouve alors la relation 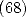 en
utilisant les séries hypergéométriques et les sommes d’Euler. Il en déduit alors quatre égalités pour
en
utilisant les séries hypergéométriques et les sommes d’Euler. Il en déduit alors quatre égalités pour 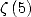 (relation
(relation 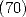 )
)
On peut établir ces quatre égalités directement à l’aide de la formule de Kummer qui s’écrit avec 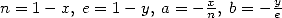
On applique alors la même démarche que pour les polylogarithmes d’ordre 4.
- Avec
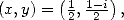 on obtient, compte tenu de
on obtient, compte tenu de
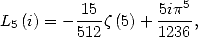
ce qui donne
Ce qui se simplifie en, en utilisant
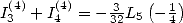
- Avec
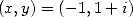 on obtient
on obtient
qui se traduit par
- Avec
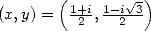 , on obtient
, on obtient
On simplifie cette égalité à l’aide de
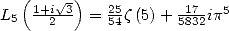 et de la formule de multiplication
et de la formule de multiplication
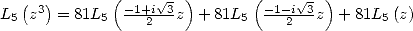 , qui avec
, qui avec 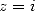 permet d’obtenir
permet d’obtenir 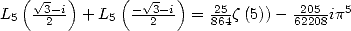 .
.
Ainsi - Avec
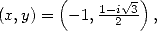 on obtient
on obtient
ce qui donne
Remarque 6 La relation 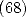 prouvée par Broadhurst ([3]) correspond au calcul de
prouvée par Broadhurst ([3]) correspond au calcul de 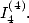 Le calcul donné ici semble beaucoup
plus simple.
Le calcul donné ici semble beaucoup
plus simple.
6.7.2 Application à la détermination de formules BBP
On considère maintenant la forme linéaire 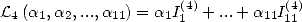 . Les résultats précédents donnent
. Les résultats précédents donnent
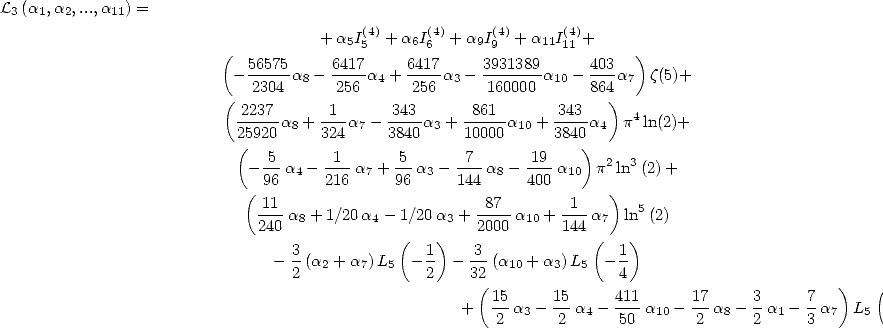 | (266) |
6.7.3 Formules pour 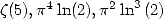 et
et 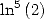
On en déduit des formules 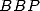 pour les constantes
pour les constantes 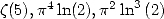 et
et 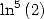 . On rappelle que les polynômes
. On rappelle que les polynômes 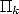 sont définis
par
sont définis
par 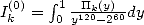 .
.
On obtient alors
avec ![[ai] = (311416,168912,239375,382643,0,0,- 168912,96489,0,-239375,0)](../mathematiciens/huvent/hyperg812x.gif)
avec ![[ai] = (22046536,11642616,15741875,26174255,0,0,-11642616,5323725,](../mathematiciens/huvent/hyperg814x.gif)
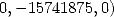
avec ![[ai] = (32556,17892,25625,40413,0,0,-17892,10899,0,-25625,0)](../mathematiciens/huvent/hyperg817x.gif)
avec ![[ai] = (12347068,6435126,8249375,14111819,0,0,- 6435126,2392497,](../mathematiciens/huvent/hyperg819x.gif)
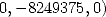
6.7.4 Simplifications de ces formules
Ces formules peuvent se simplifier en faisant apparaître le terme 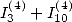 . Par exemple
. Par exemple 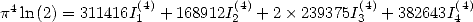
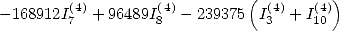 ce qui donne
ce qui donne
De même
Retour à la page d'accueil

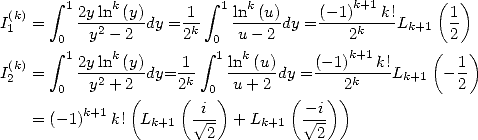
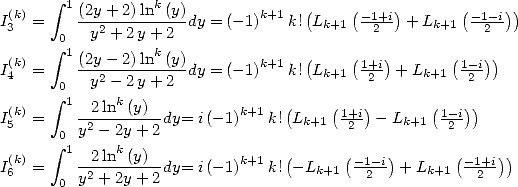
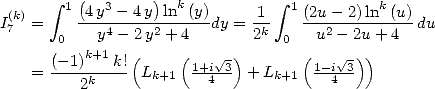
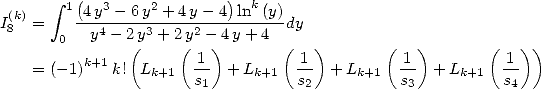
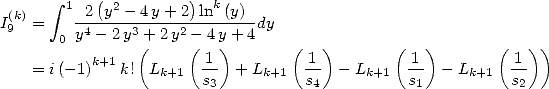
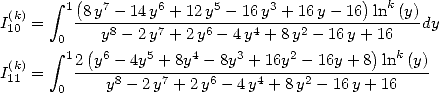
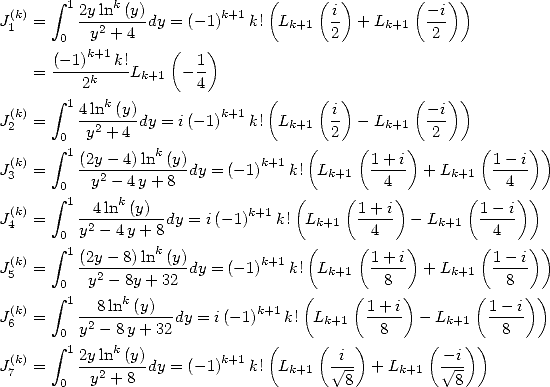
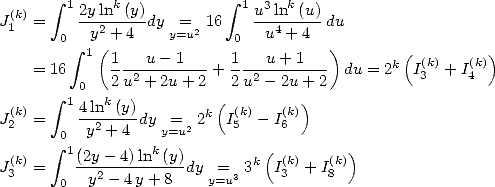
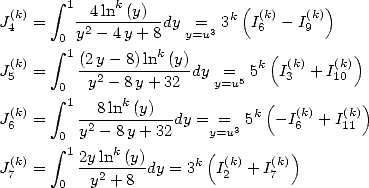
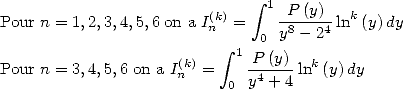
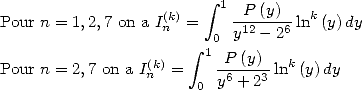
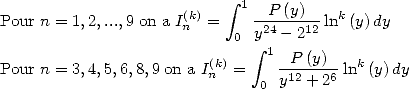
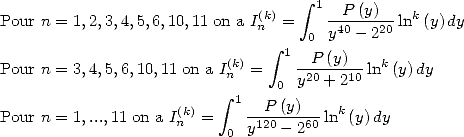
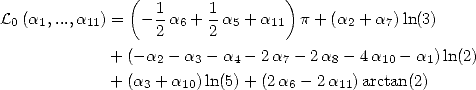
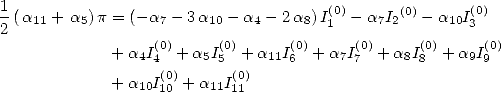
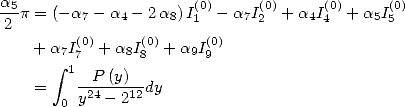
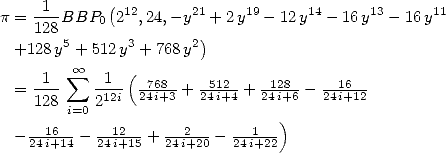
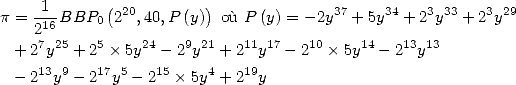
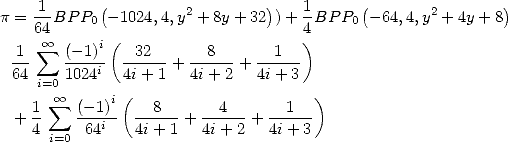
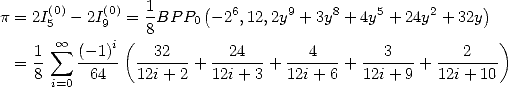
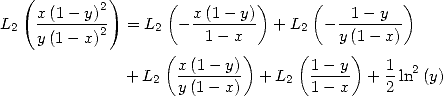
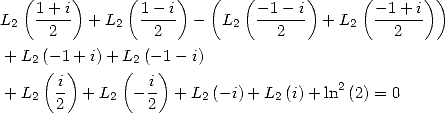
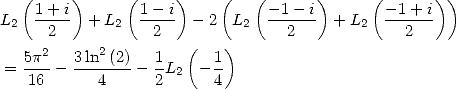
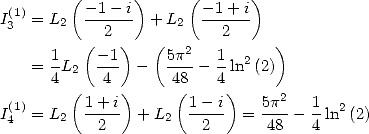
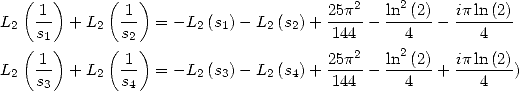
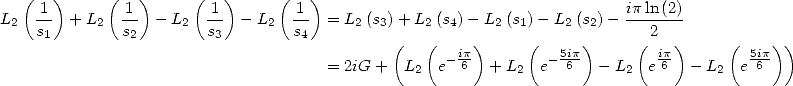
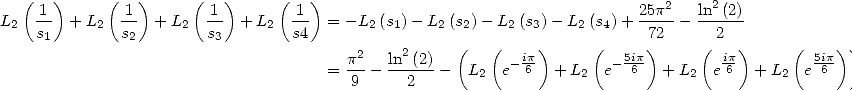
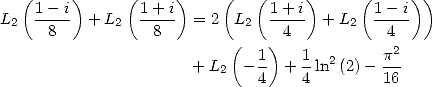
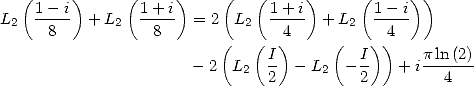
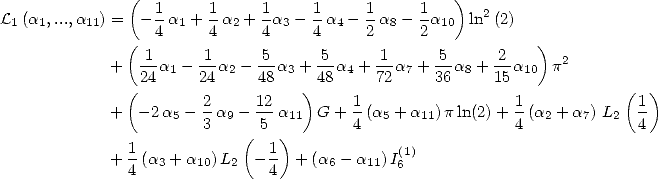
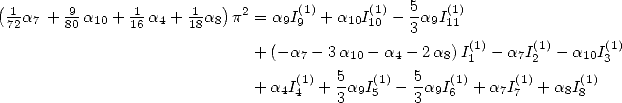
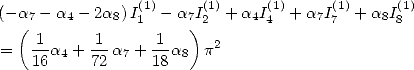
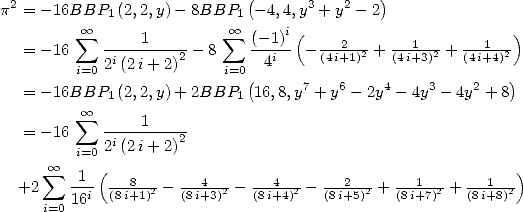
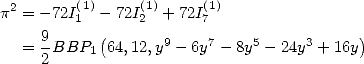
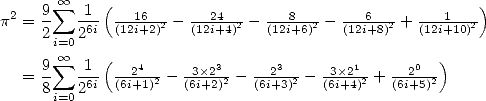
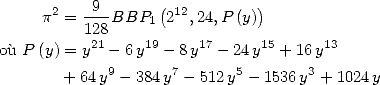
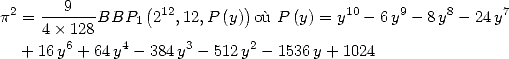

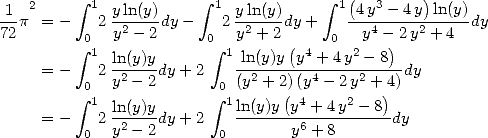
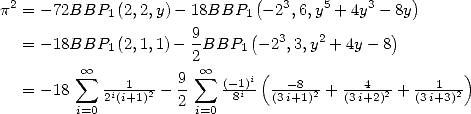
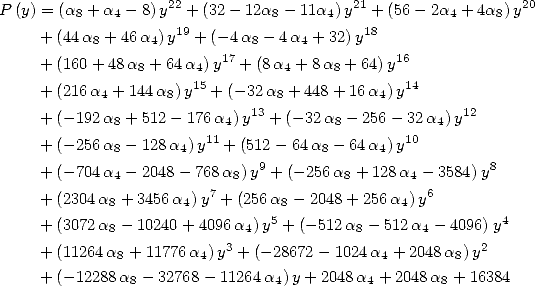
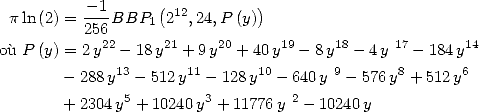
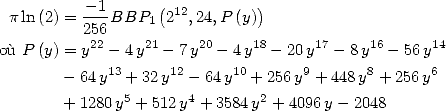
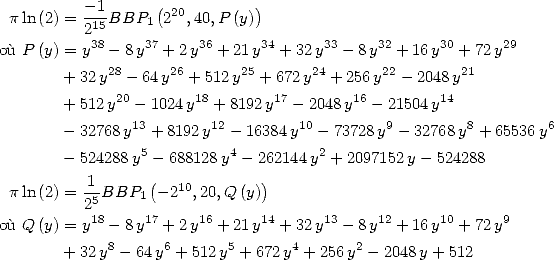
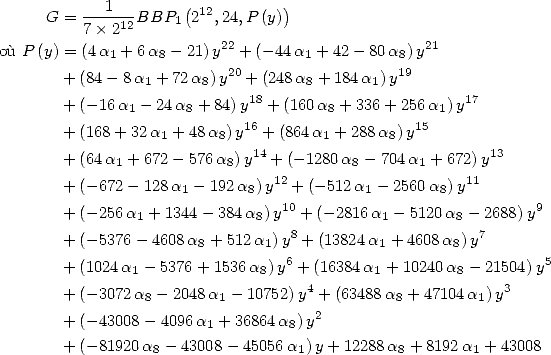
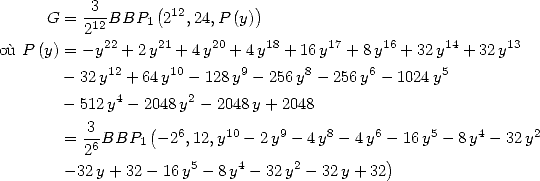
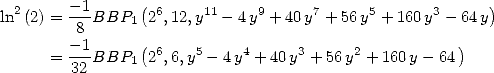
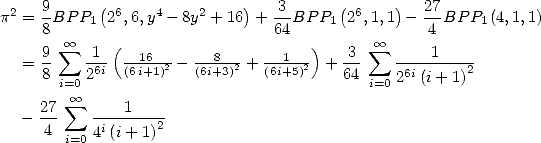
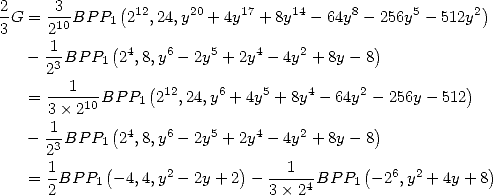
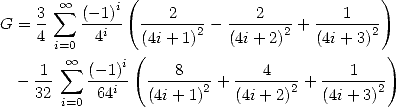
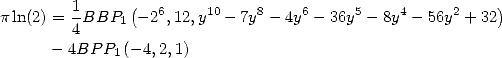
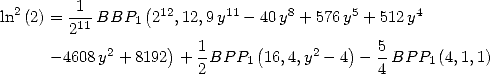
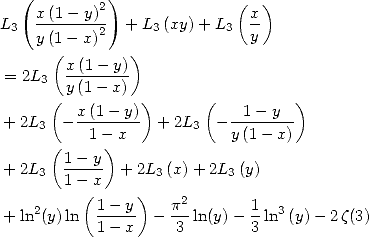
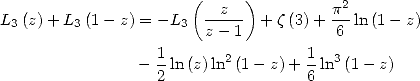
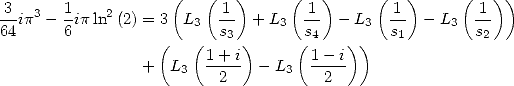
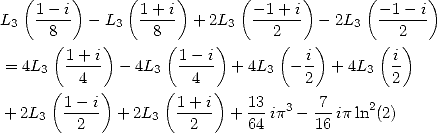
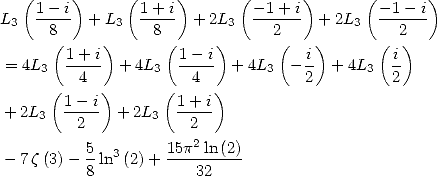
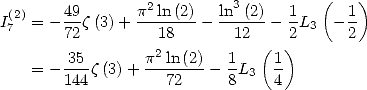
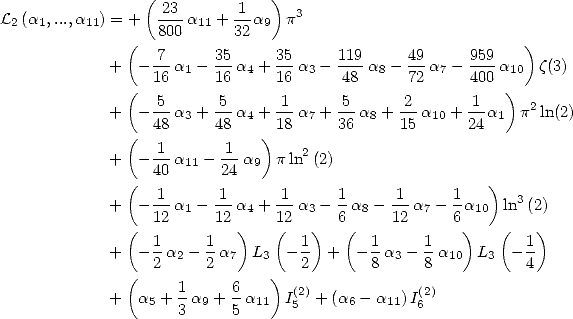
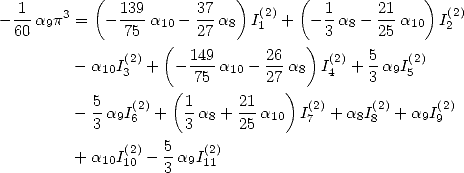
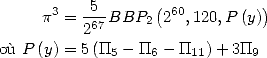
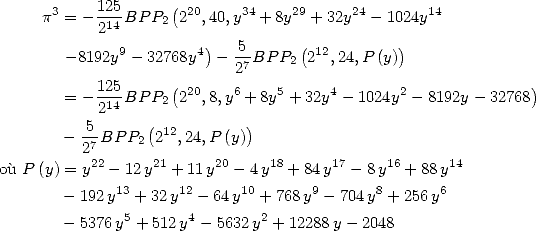
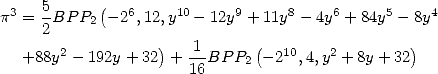
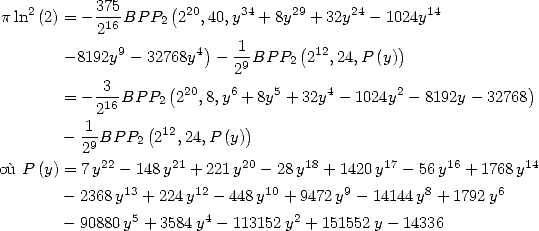
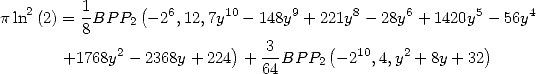
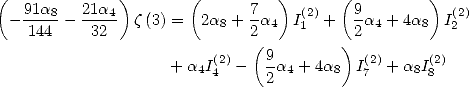
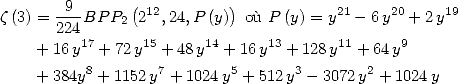
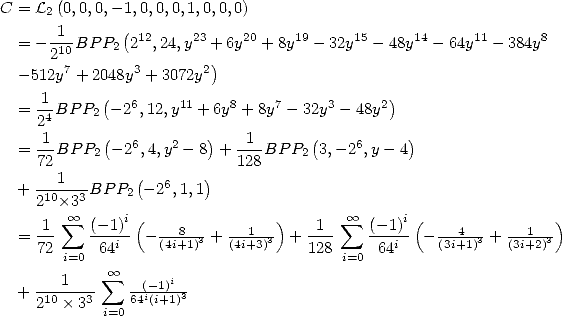
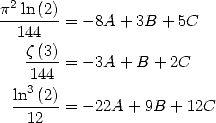
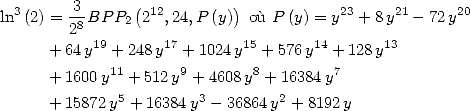
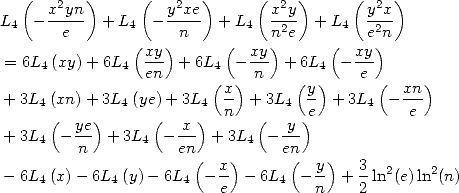
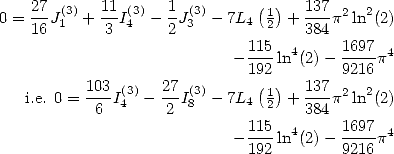
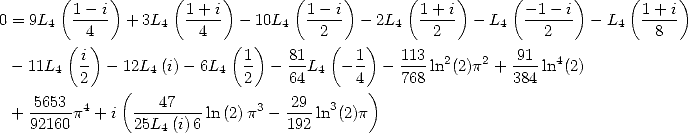
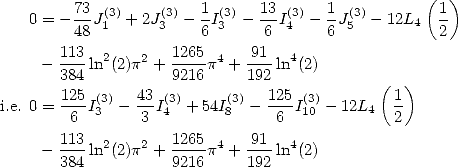
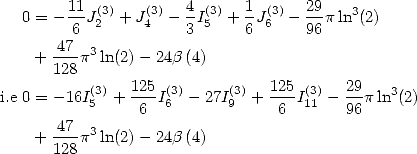
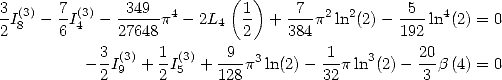
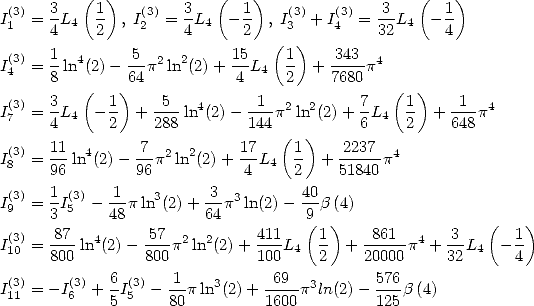
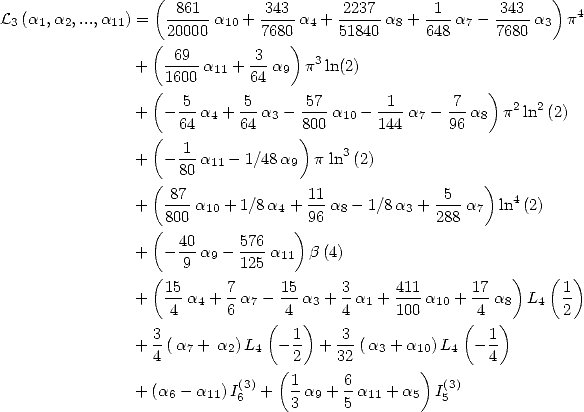
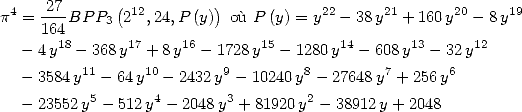
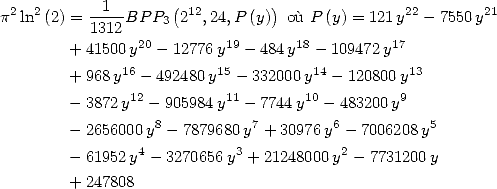
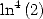
![[ai] = (-18932,- 6849,0,- 11176,0,0,6849,11322,0,0,0),](../mathematiciens/huvent/hyperg761x.gif) on obtient
on obtient