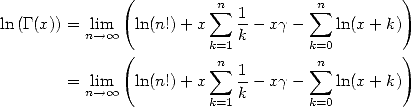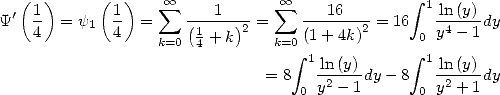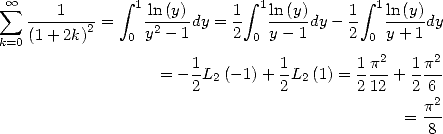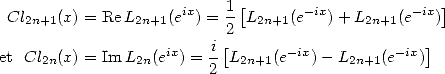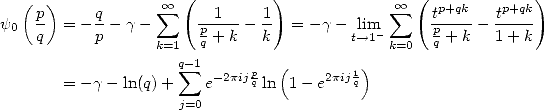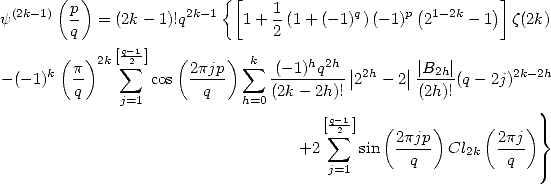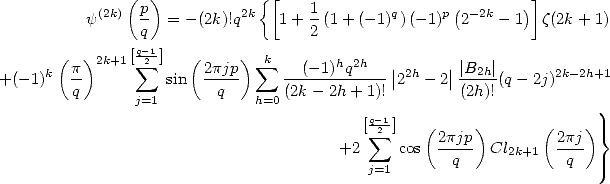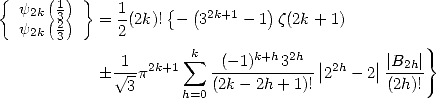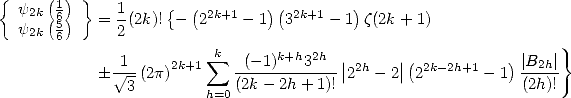9 Polygamma et Clausen

(cas entier fixé, , )

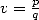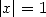Une autre plongée dans les cas particuliers de la fonction 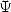... On commence à mieux cerner le problème !

9.1 Fonctions polygamma

Les fonctions polygamma sont définis pour 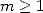par la relation :

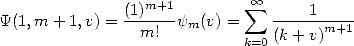(307)

On a donc bien affaire à des séries hypergéométriques :

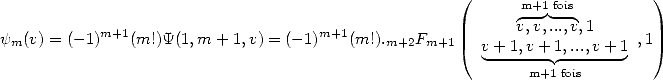(308)

On remarquera que pour 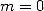, la série n’est pas convergente, c’est pourquoi on ne peut utiliser cette définition.

Cependant, si j’ai introduit les polygamma apr leurs séries pour faire le lien avec ce qui nous intéresse ici, il faut bien savoir que la définition usuelle des polygamma se fait en utilisant justement la célèbre fonction Gamma 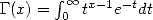. Ainsi les fonctions 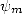sont en fait les dérivées 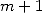-ièmes du logarithme de la fonction Gamma :

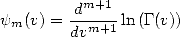(309)

et l’on peut définir 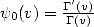que l’on appelle aussi la fonction Digamma. Pourquoi tout cela au fait ?

En fait, je suis parti de la jolie formule rappelant la fonction mais il me parait utile de montrer rapidement pourquoi tout cela est lié à la fonction . Car tout de même, cette fameuse série hypergéométrique ne donne souvent que du , même caché !

Partons de l’égalité bien connue 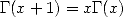pour nous confirmer et rappeler que la définition du symbole de Pochammer nous fournit pour tout 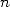dans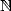

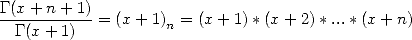(310)

soit la formule suivante

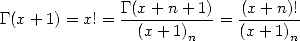(311)

Grâce à la non moins fameuse équivalence de Stirling étendue à la factorielle non entière on a pour 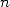proche de l’infini

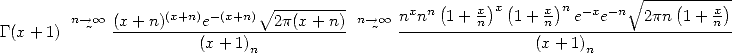(312)

en décomposant et en sortant le 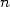. Ensuite, on remarque que 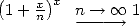et que  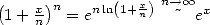et enfin que bien sûr 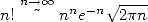grâce à Stirling. Ceci nous amène à

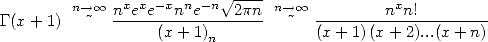(313)

soit

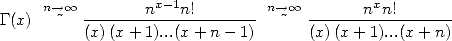(314)

Ceci nous donne la version logarithmique de la fonction Gamma

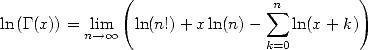(315)

qui est équivalente à la formulation de la fonction par le produit infini de Weierstrass pour les intimes. En effet, en prenant en compte que 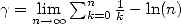, on peut écrire

A partir de là, on peut partir dans de folles dérivations (dont nous tairons la justification rigoureuse par souci de légèreté) et retrouver facilement les fonctions polygamma et digamma communément définies. En effet, une première dérivation donne

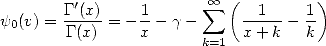(317)

puis une seconde dérivation fournit

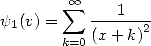(318)

et ainsi de suite.

Bref, vous l’aurez compris, on joue ici avec la fonction Gamma et ses dérivées.

9.2 La fonction digamma

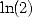Nous avons vu la définition de la fonction digamma plus haut (317). Celle-ci est intéressante dans la mesure où lorsqu’elle fait faire intervenir du et du 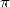, elle ne parvient pas à y associer la constante gamma d’Euler. Ainsi, on a

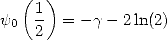(319)

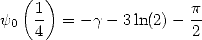(320)

De par la formule 317, la constante 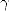se simplifie... Est-ce à dire que cette constante n’est pas homogène à 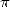ou 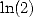 ? c’est probable... D’après les polygamma et les formules BBP, on pourrait dire que si 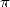est d’ordre 1 et 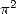est d’ordre 2, alors 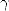est d’un ordre ”” ou en dessous de 1 en tous les cas...

Aux points rationnels, la fonction digamma nous dévoile son intimité grâce au théorème du digamma de Gauss, qui dit que

(321)

pour , .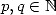

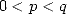On voit bien ici l’intervention de 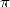, toujours présent aux grands rendez-vous !

9.3 Polygamma d’ordre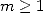

Plouffe a mis en évidence sur sa page de nombreuses relations entre les fonctions polygamma d’ordre 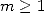et les constantes d’ordre 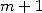pour des paramètres rationnels.

9.3.1 Liens avec les intégrales des formules BBP

Bien que ces relations aient été mises en évidence plus tardivement, ceci n’est rien d’autre que les formules BBP sans puissance 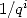. En effet, cela revient à prendre une intégrale particulière, et plus précisément 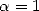dans la formule 64.

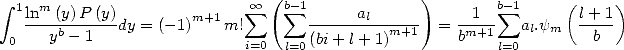(322)

Pour cette raison, les démonstrations des formules se font exactement de la même manière que dans le paragraphe consacré aux formules BBP.

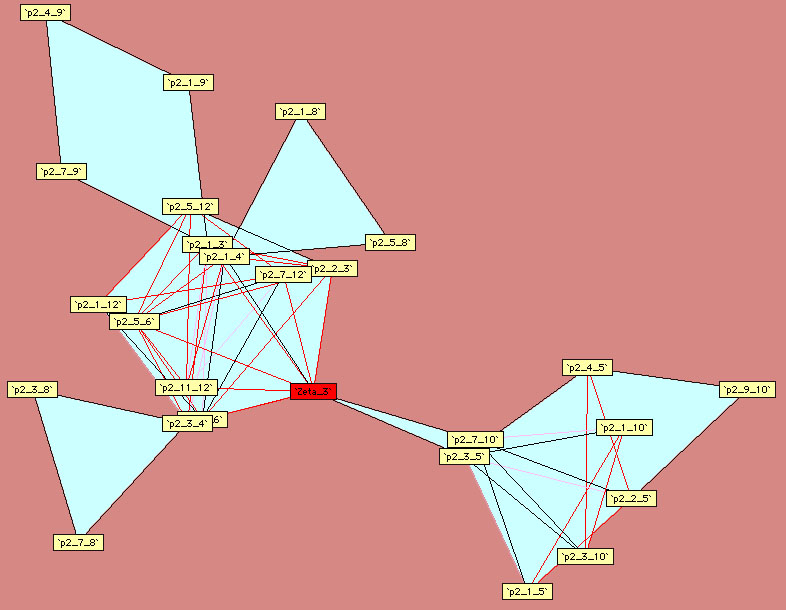
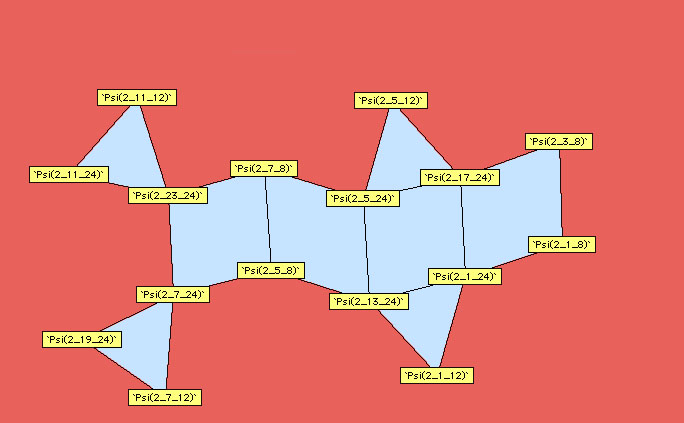
9.3.2 Une approche graphique

Plouffe a approché les relations linéaires d’un autre point de vue que les formules classiques, c’est celui du lien linéaire. En effet, en cherchant systématiquement les relations pour les polygamma d’ordre 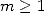pris aux valeurs rationnelles avec de petits dénominateurs, on peut construire des schémas synthétisant les liens entre polygamma d’un même ordre. Il suffit de suivre le chemin du trait pour observer quelles constantes sont liées linéairement entre elles.

En ce qui concerne les notations, on remarquera que la dérivée de la fonction digamma est la fonction polygamma d’ordre 2 : 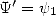pour comprendre les notations de Plouffe .

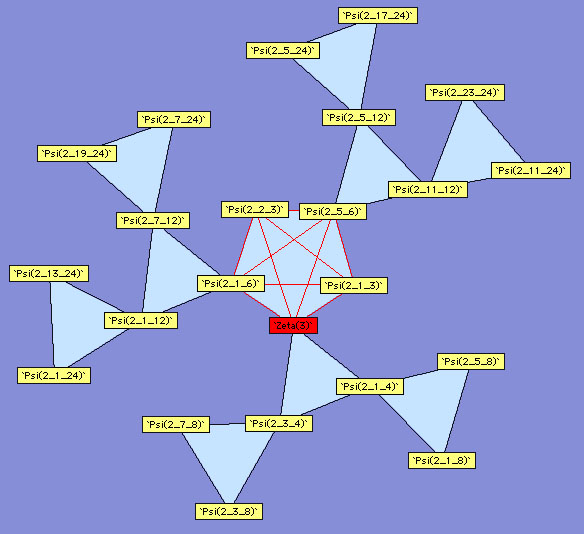
Un premier exemple est fourni avec les constantes 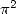et 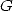(constante de catalan) qui est d’ordre 2 comme on le sait :

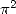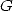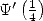Ici, il faut comprendre que le circuit entre , , et est fermé puisqu’ils forment un triangle. Ainsi, numériquement, on a en effet

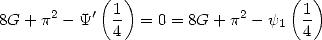(323)

Comme le dit Plouffe , il faut noter que si l’on introduisait 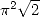, on trouverait sans doute d’autres diagrammes ou d’autres branches de diagrammes existants.

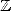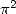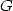Je reprends aussi ses commentaires, que du bon sens, qui indiquent par exemple sur ce diagramme que l’on ne peut apparemment pas trouver de relation dans entre , , et 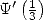, mais rien ne dit que c’est valable dans d’autres domaines, justement avec 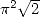ou des choses dans ce genre.

La symétrie qui apparait dans ce schéma (et parfois d’autres) est souvent due à des formules analytiques de symétrie, ici par exemple, on a

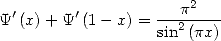(324)

ce qui fournit bien des relations rationnelles au moins pour .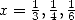

Enfin, quelques liaisons entre polygamma rationnels sans 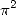ou ne sont pas retranscrites ici, pour éviter certains confusions dans le diagramme.

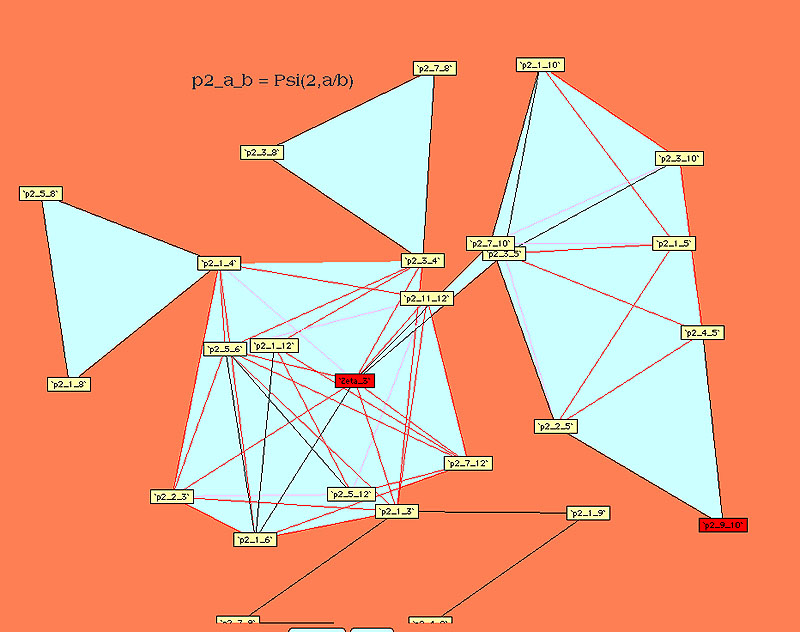
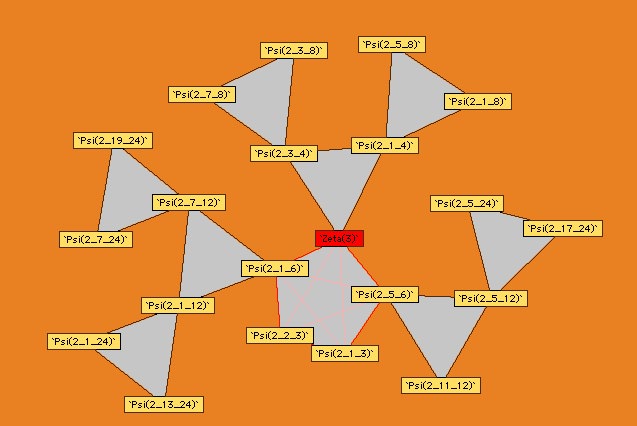
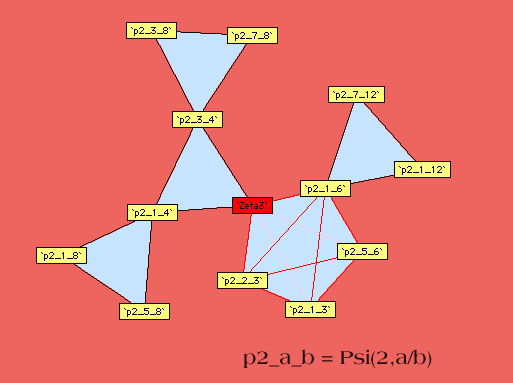
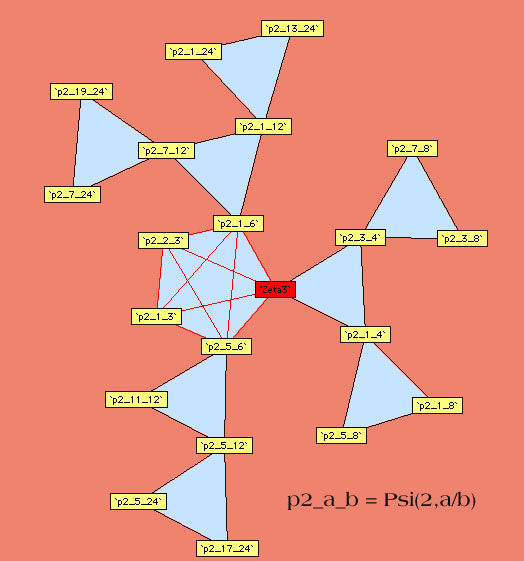
Voici les autres diagrammes construits par Plouffe  :

Ordre 2

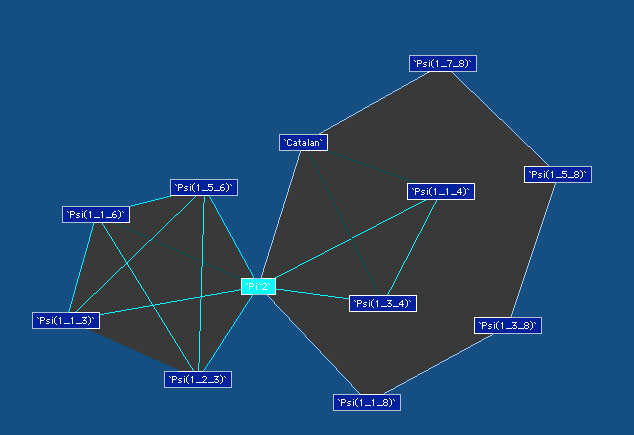
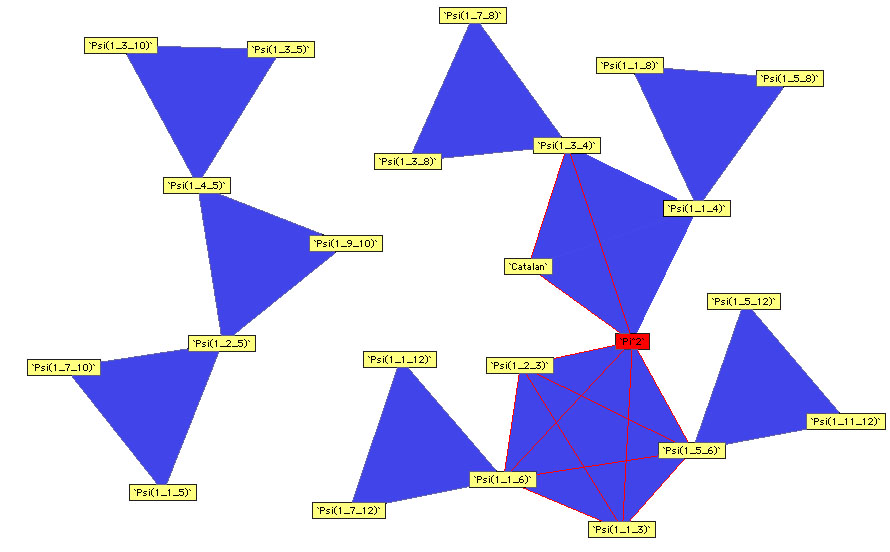
Ordre 3

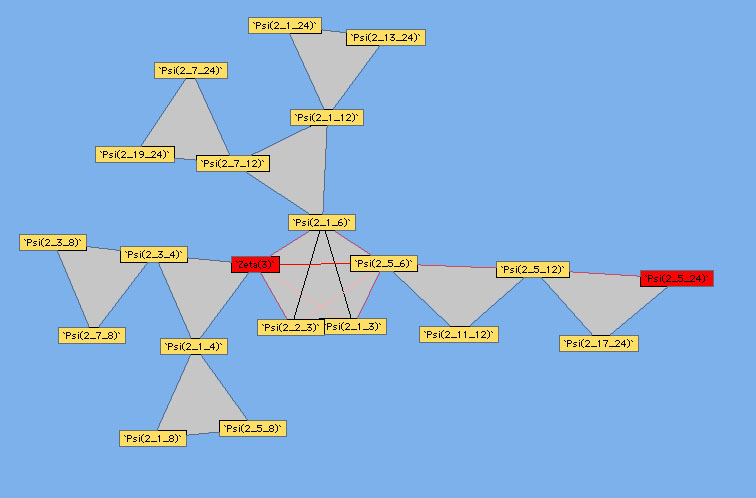
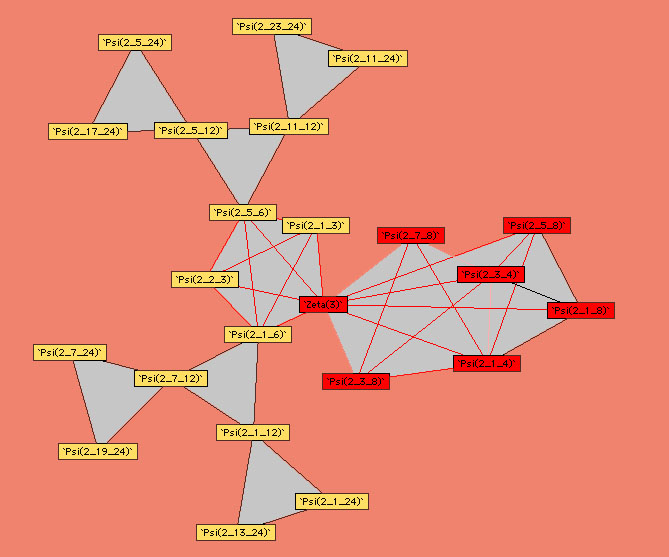
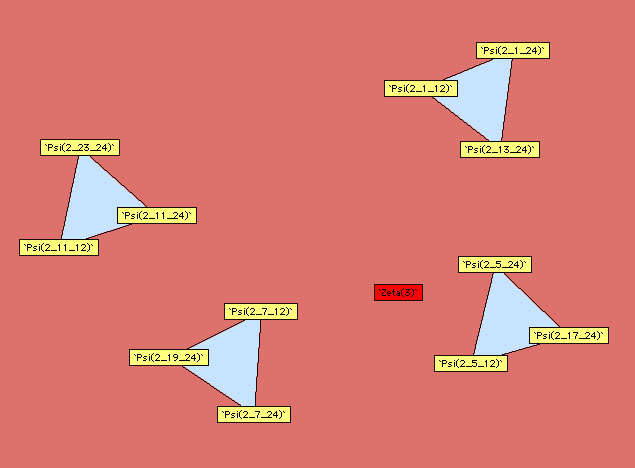
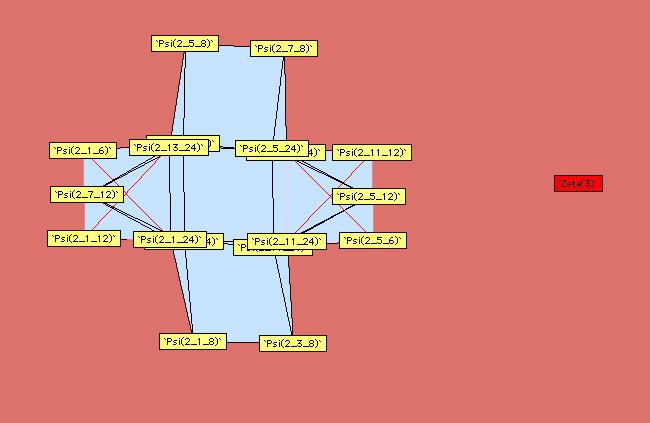
9.3.3 Traduction analytique

Voici quelques exemples de relations, où l’on voit également apparaitre le dilogarithme ! On  pourra retrouver l’ensemble des relations découvertes par Plouffe à cette page et naviguer parmi les sections consacrées à la constante gamma d’Euler, à 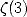, etc...

Ordre 2

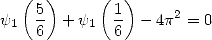(325)

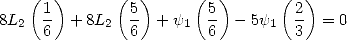(326)

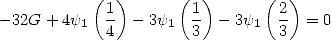(327)

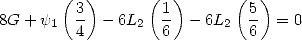(328)

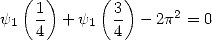(329)

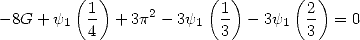(330)

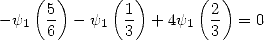(331)

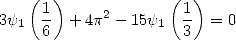(332)

(333)

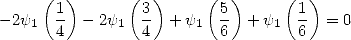Ordre 3

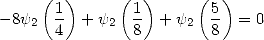(334)

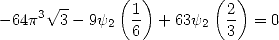(335)

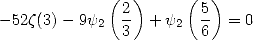(336)

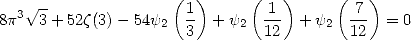
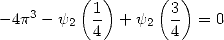
entre autres...

Démonstrations Voici la preuve d’une formule, pour l’exemple :

La plus connue est certainement

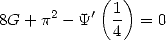(337)

Preuve. La preuve utilise ici la série et la représentation intégrale. On peut déjà noter en effet que

d’après la forme de l’intégrale équivalente (voir 322), soit en équivalent série

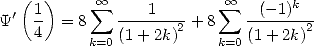(339)

Le membre de droite est la définition de la constante de Catalan 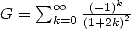. Pour le membre de gauche, deux options possibles, on peut repasser par la forme intégrale pour retrouver des dilogarithmes bien connus

On peut aussi voir cela plus directement par manipulation de la série d’Euler

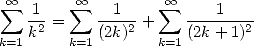(341)

en coupant la série selon les pairs et impairs, soit

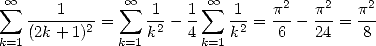(342)

A partir de là, on a bien 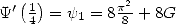et la relation annoncée.  _

Ce genre de preuve facile mais caractéristique se retrouve dans toutes les relations de cette section. On bidouille la série, ou l’on revient aux intégrales (voire un peu des deux !). C’est souvent plus facile que pour les formules BBP proprement dites car l’intégrale considérée est toujours entre 0 et 1 (sous sa forme usuelle).

9.4 Combinaisons de Kölbig

Une approche puissante provient d’un article fondateur de K.S. Kölbig [15] qui met en relation les polygamma et les fonction de Clausen. Une petite présentation s’impose !

9.4.1 Fonctions de Clausen

Les fonctions de Clausen sont définies par des séries qui semblent tout de suite intéressantes !

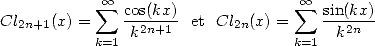(343)

On a en effet immédiatement

La dissimétrie de la définition (pourquoi ne pas considérer 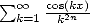 ?) provient du fait que pour les parités opposées, les formules sont calculables explicitement par diverses méthodes classiques d’intégration et d’analyse... Par exemple, on a

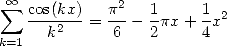(345)

ou encore

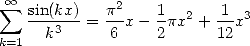(346)

C’est un des jolis problèmes mathématiques de comprendre pourquoi cela ne se passe pas aussi bien dans les deux cas ! C’est un écueil équivalent à celui qui concerne les valeurs paires et impaires de la fonction 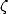de Riemann.

Un résultat classique (puisqu’il en existe tout de même !) est que

(347)

ce qui est une bonne façon de lier les deux constantes !

Les fonctions de Clausen sont connues pour être exprimables en fonction de constantes connues uniquement pour un petit nombre de valeurs de . Ce qui n’est pas très enthousiasmant a priori... Mais nous allons voir qu’en passant par les fonctions polygamma, on peut parfois au moins les relier à quelque chose !

9.4.2 Les résultats de Kölbig.

Introduction Pour arriver aux résultats de Kölbig, on peut tout d’abord remarquer qu’une intégration fournit

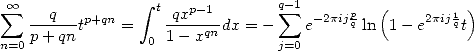(348)

par décomposition de la fraction en éléments simples. La relation est valable pour 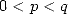. C’est une autre manière de voir les formules BBP, non dénuée d’intérêt puisque dans cette présentation, on voit par exemple que la nature des constantes qui interviennent n’est pas déterminée par le coefficient 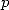, celui-ci étant une simple pondération devant le logarithme. Il parait que la relation est due à Jensen et peut être prouvée en développant le logarithme ! Moi je ne vois pas où était la difficulté en passant par la décomposition en éléments simples, mais peut-être me trompé-je ?

Ensuite, la relation de continuité d’Abel permet d’écrire que pour la fonction digamma,

Voilà.

Ordres supérieurs Et en fait, Kölbig a obtenu des résultats tout à fait similaires, mais sur les dérivées de la fonction digamma, que l’on sait être les polygamma. Au lieu d’avoir des logarithmes, on a des polylogarithmes (logique !) et au lieu d’un logarithme fonction de l’exponentielle complexe, on a des polylog de l’exponentielle complexe, que l’on sait justement être des fonctions de Clausen d’après 344 ! Tout ceci est donc très cohérent et fournit les relations de Kölbig suivantes

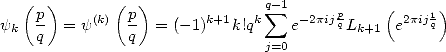(350)

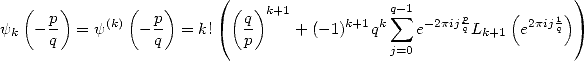(351)

qui se prouvent directement depuis la définition des polylogarithmes en sommant sur  :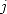

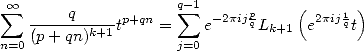(352)

On pourra remarquer que l’on obtient la fameuse formule de multiplication des polylogarithmes en faisant 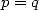dans cette équation, c’est sympa !

Je ne vais pas rentrer dans les détails des neuf pages de la partie démo de l’article de Kölbig mais le principe est ensuite le suivant : comme le membre de gauche est réel, on prend la partie réelle du membre de droite et l’on calcule la dérivée de 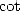qui apparait. En considérant la relation d’inversion généralisée, et en utilisant le fait que

(353)

pour 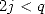, on obtient finalement que

Théorème 15 de Kölbig

Pour , ,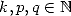

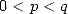et pour les ordres pairs, pour , ,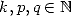

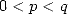où 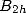est le nombre de Bernoulli d’indice .

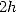Des applications Plus haut (342), on a montré que

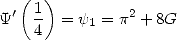(356)

mais on peut aussi noter que l’on a

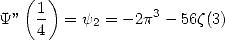(357)

ce qui permet d’obtenir les valeurs pour 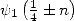et 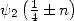à partir des formules de récursion

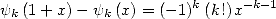(358)

et de réflexion

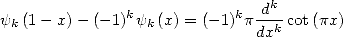(359)

mais le principal intérêt de ces formules est de fournir des valeurs pour 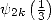, , 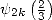, 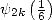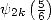en fonction de constantes bien connues ! Pour ,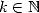

On retrouve ainsi les relations (325), (331), (332), (335) et (336) données par Plouffe .