|
|
|
|
|
15 Autres formules hypergéométriques concernant 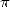
Il existe plein de formules hypergéométriques liées à 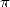 , par exemple
, par exemple
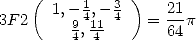 | (715) |
que j’ai trouvée, ou
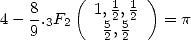 | (716) |
que j’ai lue. Les formules de Ramanujan ou Chudnovsky peuvent également s’écrire sous la forme de fonctions hypergéométriques. Le problème est de s’y retrouver dans les coefficients, les formules hypergéométriques ont un peu trop de paramètres libres ! Bref impossible de tirer une généralisation facile de tout cela.
Conclusion 27 Bien entendu, cette page est amenée à évoluer au gré de mon courage, de dernières trouvailles, ou bien de vos idées
ou contributions ! Mon objectif premier a été de vous montrer comment une certaine forme d’intégrale, qui est très souvent équivalente
à une série hypergéométrique, peut donner une famille de constantes que l’on discerne mieux maintenant : 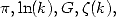 etc...
etc...
Ce sujet très actuel est sans aucun doute amené à se clarifier et unifier au cours des prochaines années. Ce n’est pas forcément
très difficile (du moins tel que je l’ai présenté !) mais cela représente des pistes fécondes, nombreuses et parfois un peu oubliées de
nos chers mathématiciens !
Retour à la page d'accueil
