|
|
|
|
|
1 Petit rappel historique rapide
Les formules de Machin , et même de Plouffe sont des cas particuliers de séries hypergéométriques (mais il est vrai que ce ne sont pas les plus
intéressantes, celles qui profitent le plus de la structure d’une série hypergéométriques). Ces dernières ont beaucoup intéressé le milieu du
XIXe siècle mais restaient difficile à étudier de manière théorique en raison de la variété de leur forme. Beaucoup de résultats concernent
plutôt des relations entre familles de séries hypergéométriques comme les 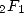 . Passionné par ces séries, Ramanujan nous a laissé nombre de
relations et formules qui semblent un aboutissement extraordinaire ! Pourtant, il reste beaucoup à faire.... même des choses plus simples !
Revenons un peu en arrière...
. Passionné par ces séries, Ramanujan nous a laissé nombre de
relations et formules qui semblent un aboutissement extraordinaire ! Pourtant, il reste beaucoup à faire.... même des choses plus simples !
Revenons un peu en arrière...
Après la série de Bailey-Borwein-Plouffe en 1995, on pouvait penser que de nombreux résultats similaires allaient apparaitre rapidement,
mais après la formule de Bellard en 1997, l’enthousiasme semble un tout petit peu retombé car les mathématiciens butent contre
l’impossibilité de trouver une formule en base 10 pour Pi. Un algo astucieux de Plouffe et une amélioration de Fabrice Bellard permettent
bien de calculer n’importe quelle décimale de Pi sans connaitre les autres, mais la vitesse et la simplicité ne sont pas les mêmes... Ils se
tournent alors de plus en plus vers la recherche d’une exploitation de ces résultats pour démontrer la normalité de Pi. Quoi
de plus beau en effet qu’une formule fournissant au moyen d’un calcul assez simple n’importe quel digit de Pi ou d’un
logarithme en base 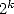 sans connaitre les précédents, pour étudier la répartition de ces digits ? L’intuition était belle et David
Bailey avec Richard Crandall semblent proches du résultat bien qu’une conjecture difficile reste à résoudre (voir article
[11]).
sans connaitre les précédents, pour étudier la répartition de ces digits ? L’intuition était belle et David
Bailey avec Richard Crandall semblent proches du résultat bien qu’une conjecture difficile reste à résoudre (voir article
[11]).
Mais concernant les formules proprement dites, seul David Broadhurst [3] semble principalement continuer l’exploration depuis 1998, soulignant d’ailleurs de plus en plus le lien des représentations des formules BBP avec les ”ladder” comme ils disent en anglais des polylogarithmes et des relations de Kummer (quand il ne met pas en évidence l’apparition des polylogarithmes dans la physique des diagrammes de Feynman !). J’ai d’ailleurs trouvé en 2000 des formules BBP pour Zêta(3) (démontrée) et pour la constante de Catalan, qui semblent figurer implicitement dans les articles de Broadhurst, mais rien n’est sûr... Gery Huvent (avec qui je discute quasi-quotidiennement à certaines périodes !) réalise en 2000 et 2001 [12] une exploration théorique systématique des premiers ordres des séries BBP, avec des outils classiques de l’analyse, ce qui unifie beaucoup de choses de manière remarquable. Evidemment, plus on monte en ordre (en combinaisons multiplicatives de constantes), plus les résultats deviennent ardus à obtenir mais très intéressants tout de même...
Gery méritait bien d’avoir sa page sur ce site, pour ses qualités mathématiques et parce que nos discussions m’apportent beaucoup. Alliant mon enthousiasme exploratoire à ses idées fécondes, je trouve que nous avons bien progressé chacun dans notre compréhension du domaine, même si certains développements théoriques de Broadhurst ou de récents articles sont vraiment impressionnants. Ces pages sont donc un certain hommage à Gery Huvent , qui a écrit disons une bonne moitié de ce que vous lirez dans ces pages.
Et puis prenant le relais des formules BBP qui semblent maintenant mieux comprises, les formules factorielles, comprenez avec des
combinaisons, applications directes de séries hypergéométriques, viennent prendre le relais ! William Gosper avait ouvert la voie ainsi que le
fameux Comtet en 1974 par exemple, mais grâce à l’étude de quelques familles d’intégrales, on arrive à comprendre de mieux en mieux les
séries du genre 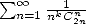 et donner une réponse maintenant à des questions qui ont empoisonné l’intuition de bon
nombre de spécialistes pendant plusieurs années (par exemple pourquoi on ne trouvait pas de relation simple entre
et donner une réponse maintenant à des questions qui ont empoisonné l’intuition de bon
nombre de spécialistes pendant plusieurs années (par exemple pourquoi on ne trouvait pas de relation simple entre 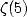 et
et
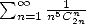 ...).
...).
Gery Huvent explore une fois encore le domaine en 2001 et de mon côté je découvre nombre de formules factorielles que je croyais nouvelles mais qui sont publiées ici deux mois après un article ( [7]) qui explique les fondamentaux de la découverte de ce type de formule... Je complète cet article par une exploration des formules binomiales BBP et de la méthode de la fonction Bêta, avec Jesus Guillera, qui généralise d’une certaine manière les formules BBP [13] et tente d’unifier l’écriture des séries sous forme BBP.
Les séries à coefficient harmoniques sont également un domaine intéressant, dont le lien avec les formules BBP est clair grâce à la représentation intégrale de la fonction génératrice des sommes harmoniques. Par contre, les séries à coefficients harmoniques ne sont pas des séries hypergéométriques (à ma connaissance...), mais méritent d’apparaitre ici en raison de leurs jolis résultats très similaires !
Tout ceci dans le cadre des séries hypergéométriques que je vais vous présenter tout d’abord pour fixer les idées côté séries... Il faut bien noter que l’élément fédérateur de toutes ces formules est la représentation intégrale équivalente, dont une forme simplifiée sera toujours du type
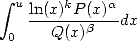
où 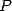 et
et 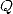 sont des polynômes sur
sont des polynômes sur ![Q[X]](../mathematiciens/huvent/hyperg83x.gif) ,
, 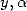 et
et 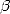 sont des rationnels. Cependant, à part pour les démonstrations, je ne
privilégierai pas de plan structurel autour de cas particuliers de ces intégrales, d’abord parce qu’historiquement, ce n’est pas ce qui a prévalu,
et qu’ensuite les séries ont traditionnellement un réel intérêt calculatoire ou théorique, comme les formules BBP, ce dont ne peut se vanter
une austère intégrale à première vue, même si elle est équivalente à la série ! Le problème des intégrales est de ne pas parler immédiatement
de ce qu’elle va donner comme résultat... Enfin, les séries hypergéométriques ont un nom, alors que ce type d’intégrales n’en a pas à ma
connaissance...
sont des rationnels. Cependant, à part pour les démonstrations, je ne
privilégierai pas de plan structurel autour de cas particuliers de ces intégrales, d’abord parce qu’historiquement, ce n’est pas ce qui a prévalu,
et qu’ensuite les séries ont traditionnellement un réel intérêt calculatoire ou théorique, comme les formules BBP, ce dont ne peut se vanter
une austère intégrale à première vue, même si elle est équivalente à la série ! Le problème des intégrales est de ne pas parler immédiatement
de ce qu’elle va donner comme résultat... Enfin, les séries hypergéométriques ont un nom, alors que ce type d’intégrales n’en a pas à ma
connaissance...
Sur cette page, je reprendrai en détail les points présentés ci-dessus, avec d’autres séries classiques des mathématiques, en les replaçant par rapport aux séries hypergéométriques ou aux intégrales, pour tenter de vous donner une vue un peu plus précise du domaine très très fécond qui est exploré ces temps-ci !
Si vous n’êtes pas familier des notations hypergéométriques, je vous conseille ardemment de lire la page d’introduction aux séries hypergéométriques.
Encore une chose, la ”propriété intellectuelle” de toutes ces séries est souvent difficile à reconstituer. Certaines séries simples sont certainement connues depuis le temps que ce genre d’intégrales est manipulé, mais sans référence précise, tandis que d’autres ont peu de chances d’avoir été rencontrées. J’essaierai le plus souvent de préciser à côté de la formule celui qui me l’a montrée en premier, pour dire les choses directement, mais si vous possédez une référence plus ancienne, n’hésitez pas à me le faire savoir !
Retour à la page d'accueil
