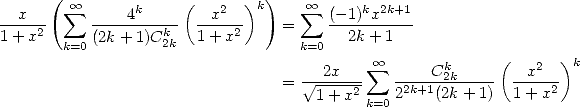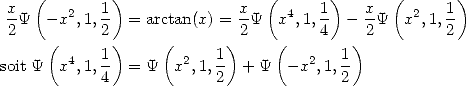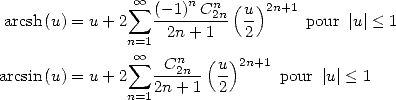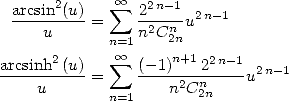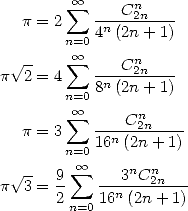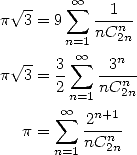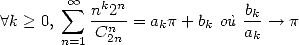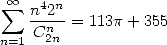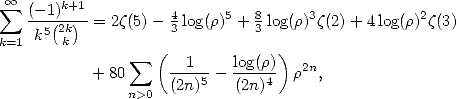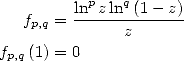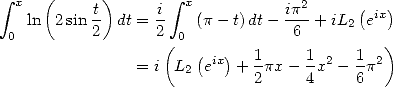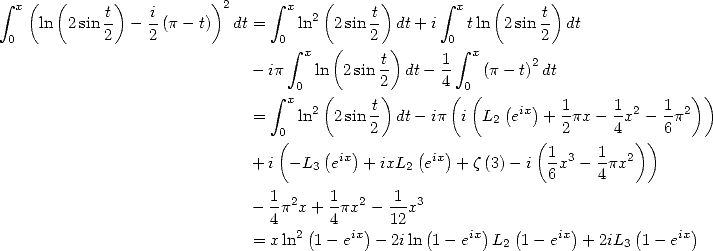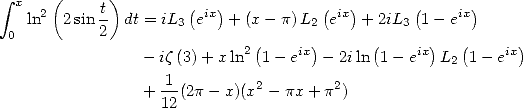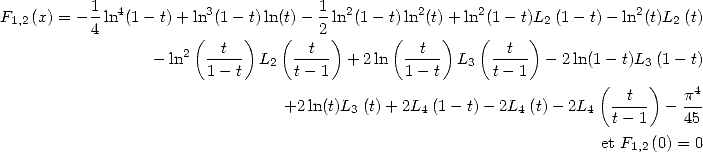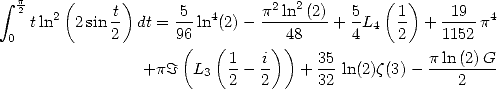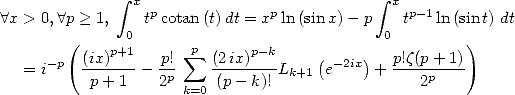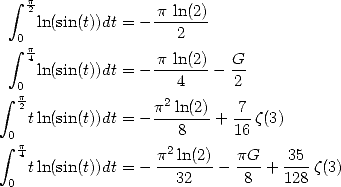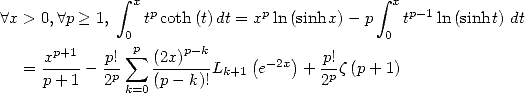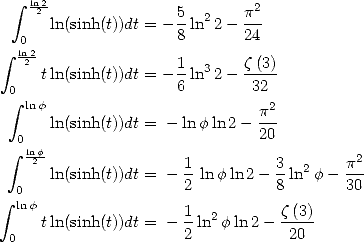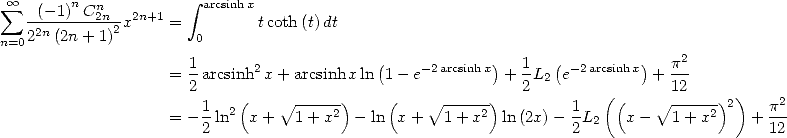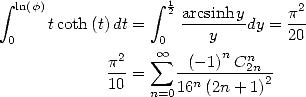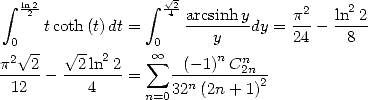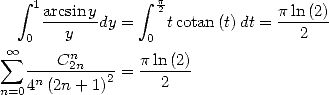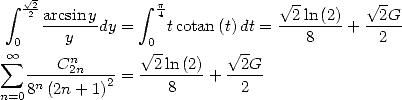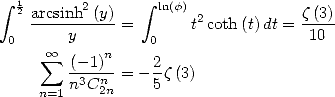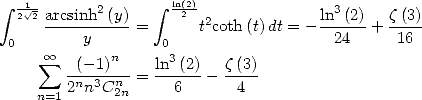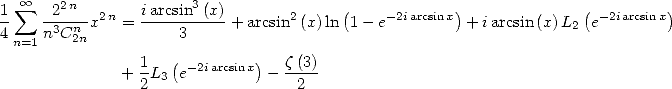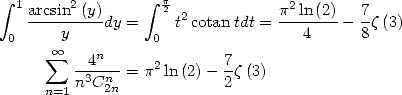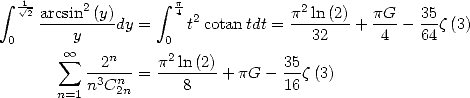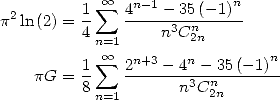|
|
|
|
|
11 Séries binomiales centrales
Un cas particulier intéressant et pas encore trop dur des séries factorielles concerne l’introduction des coefficients binomiaux centraux dans les séries. Après quelques remarques sur ces séries dans la première section, on attaquera les choses sérieuses avec plusieurs formules et leurs démonstrations !
11.1 Inversion de combinaisons
Une chose amusante est que l’on peut obtenir des séries donnant le même résultat mais dans un cas avec un coefficient binomial central central au numérateur, et dans l’autre cas au dénominateur ! Cela confirme également pourquoi on obtient le même type de résultats avec une série sans combinaison et une série avec combinaisons :
Prenons l’exemple de la fonction 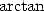 : dans un premier temps, on a la formule classique
: dans un premier temps, on a la formule classique
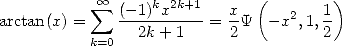 | (372) |
On sait depuis Euler (voir page Euler) que la fonction arctan s’exprime aussi selon
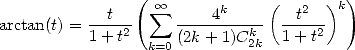 | (373) |
Enfin, la relation 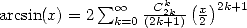 couplée à
couplée à 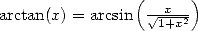 fournit
fournit
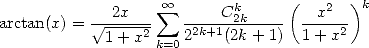 | (374) |
Une relation entre les différentes séries avec coefficients binomiaux centraux est donc l’arctan :
Etonnant, non ? ! !
En dérivant la série du centre selon  , on peut par exemple trouver l’expression sous forme de combinaison de
, on peut par exemple trouver l’expression sous forme de combinaison de 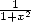 .
.
Et donc à partir de cette série, on peut trouver les expressions des combinaisons des séries de type Machin sous forme de combinaisons de formules binomiales ! Nous verrons dans la section suivante les 11.3factorielles.
On peut toutefois signaler pour la fonction arctan
La preuve est évidente en décomposant la série en pair et impair...
D’autre part, on a aussi, toujours en jouant sur les développements en série entière
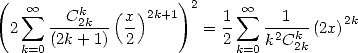 | (378) |
Enfin, on a d’après les expressions 13 et 11
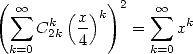 | (379) |
ce qui est assez amusant aussi !
11.2 Développements utiles
On rappelle les développements en série entières suivants qui vont nous servir au calculs de certaines séries et intégrales. :
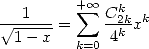 | (380) |
ce qui, en composant par 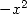 ou
ou 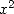 et en intégrant, donne respectivement
et en intégrant, donne respectivement
d’autre part, le développement d’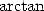 d’Euler fournit sous sa forme
d’Euler fournit sous sa forme 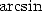
que l’on peut donc prouver par la méthode des équations différentielles.
11.3 Premières formules directes
Les quatre derniers développement de la section précédente donnent alors les séries classiques, avec 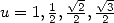
En utilisant
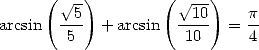 | (389) |
on peut obtenir, par exemple
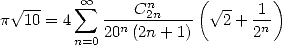 | (390) |
Avec le développement de 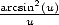 , on obtient
, on obtient
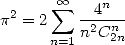 | (391) |
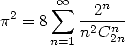 | (392) |
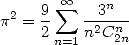 | (393) |
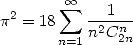 | (Euler 1748) |
Les valeur 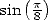 ,
, 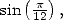
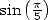 donnent les formules
donnent les formules
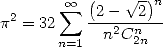 | (394) |
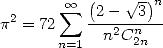 | (Grandall 1994) |
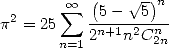 | (395) |
On peut également écrire que 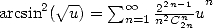 ce qui en dérivant donne
ce qui en dérivant donne
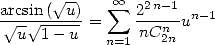 | (396) |
et obtenir d’autres séries comme
En dérivant de nouveau 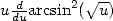 , on a
, on a
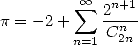 | (400) |
etc...
Sur le même modèle, Gery Huvent a proposé une conjecture qui semble ouverte, n’ayant pas lu de choses traitant du sujet...
11.4 Formules d’ordre supérieur
L’étude des séries de type 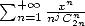 ou
ou 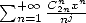 , pour
, pour 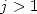 se complique un tout petit peu, car ces sommes proviennent
d’intégrations succesives des fonctions où
se complique un tout petit peu, car ces sommes proviennent
d’intégrations succesives des fonctions où 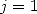 . En effet, on remarque que
. En effet, on remarque que
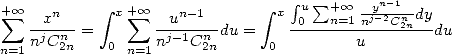 | (407) |
et ainsi de suite pour remonter par exemple jusqu’à 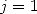 .
.
Mais bien évidemment, ces fonctions ne se laissent pas intégrer aisément ! Et il faut souvent recourir à beaucoup de patience et un peu d’astuce pour arrive à ses fins.
Cependant, les résultats sont là. On connait la formule d’Euler
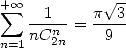 | (408) |
dont je donne une démonstration au paragraphe consacré à l’10.2calculus et à la méthode d’accélération de la convergence par les différences finies, inventée par Euler lui-même !
L’ordre supérieur, c’est une formule comme
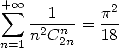 | (409) |
mais aussi
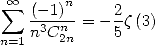 | (410) |
et la formule de Comtet datant de 1974 dont la démonstration fut laborieuse...
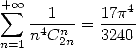 | (411) |
Evidemment, cela titillait les mathématiciens de savoir si une formule similaire existait pour l’ordre 5 ! Malheureusement, on sait
aujourd’hui que cette série ne donne pas vraiment les résultats escomptés puisque si l’on note 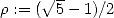 , on a en fait d’après
[8]
, on a en fait d’après
[8]
Mais cela n’empêche pas les ordres supérieurs d’être intéressants.
11.4.1 Une première formule avec démo
J’ai remarqué en aout 2001 que
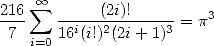 | (413) |
ce qui se traduit sous forme hypergéométrique par
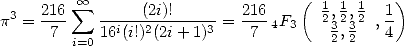
C’est sans doute une des plus simples formules factorielles et la présence du 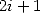 sonne comme une formule BBP. La preuve est
compliquée et liée au calcul de l’intégrale suivante
sonne comme une formule BBP. La preuve est
compliquée et liée au calcul de l’intégrale suivante
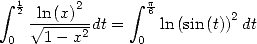 | (414) |
car le développement en série entière de 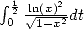 donne
donne
 dont on sait calculer les deux premiers membres.
dont on sait calculer les deux premiers membres.
On pose donc plus généralement les intégrales suivantes :
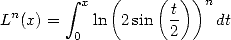 | (415) |
Notons que l’on peut clairement rapprocher cette intégrale des 9.4.1dans la mesure où 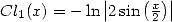 et
donc
et
donc
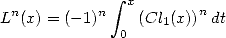
pour 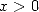 . Il n’y a pas de hasard !
. Il n’y a pas de hasard !
Le résultat qui nous intéresse est
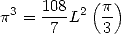
qui est équivalent à la série par un changement de variable immédiat 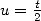 dans 414.
dans 414.
Raymon Manzoni, puis Gery Huvent , ont contribué à fournir une preuve de cette formule, c’est ce que je vous présente maintenant, en y incluant une démonstration de la formule de Comtet par Gery Huvent .
Preuve. Considérons, pour 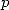 et
et 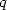 entiers
entiers 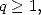 la fonction
la fonction
cette fonction est holomorphe sur
Pour ![p = 0, C\]1,+ oo [](../mathematiciens/huvent/hyperg1180x.gif)
Pour 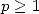
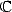 privé de
privé de ![]1,+o o [](../mathematiciens/huvent/hyperg1183x.gif) et de
et de ![]- oo , 0]](../mathematiciens/huvent/hyperg1184x.gif)
Considérons, pour ![x (- [-p,p]](../mathematiciens/huvent/hyperg1185x.gif) le chemin
le chemin ![g(t) = eit, t (- [0,x]](../mathematiciens/huvent/hyperg1186x.gif) et l’intégrale
et l’intégrale 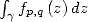 (avec
(avec 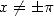 si
si 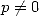 ).
).
Puisque 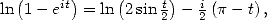 on a
on a
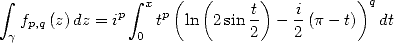 | (417) |
Si 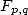 désigne une primitive de
désigne une primitive de 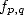 sur un domaine contenant le chemein
sur un domaine contenant le chemein 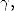 on a
on a
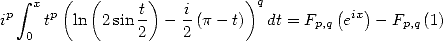 | (418) |
Le problème se ramène donc à un calcul de primitive !
La primitive de 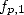 nulle en
nulle en 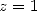 est
est
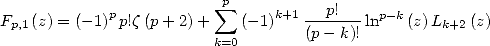 | (419) |
Ainsi
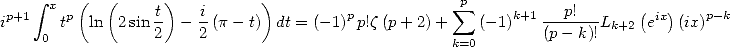
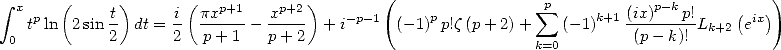 | (420) |
On obtient donc une seconde expression de 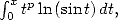 en comparant avec celle déjà obtenu, pour
en comparant avec celle déjà obtenu, pour 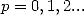 , on retrouve
simplement la valeur de
, on retrouve
simplement la valeur de 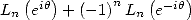 . Cela n’a rien de nouveau, car on connait le développement en séries de Fourier du
énième polynôme de bernoulli. Ce développement donne l’égalité
. Cela n’a rien de nouveau, car on connait le développement en séries de Fourier du
énième polynôme de bernoulli. Ce développement donne l’égalité
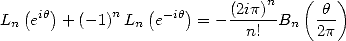 | (421) |
La primitive de  qui est nulle en
qui est nulle en  est
est
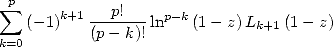 | (422) |
ainsi
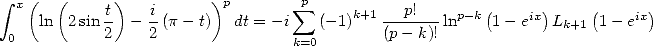 | (423) |
En particulier,
On peut retrouver que 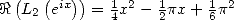 et que
et que
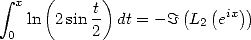 | (425) |
Et
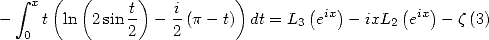 | (426) |
d’où
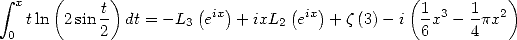 | (427) |
Puis on a
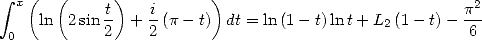 | (428) |
qui permet de retrouver la formule d’Euler pour le dilogarithme
soit
Remarque 22 On peut simplifier cette égalité avec les formules de Landen et retrouver le résultat classique
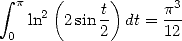 | (431) |
résultat que l’on obtient avec le développement en séries de Fourier de 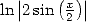 et la formule de Parseval.
et la formule de Parseval.
En particulier
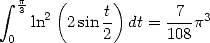 | (Gourevitch) |
car
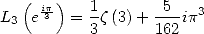 | (432) |
Cette égalité donne alors avec 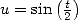 et un DSE
et un DSE
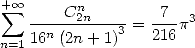 | (Gourevitch) |
On peut également établir que
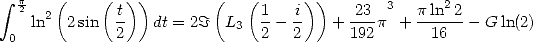 | (433) |
On peut aussi calculer la primitive de 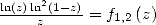 , on trouve
, on trouve
Cette égalité admet plusieurs applications :
L’égalité
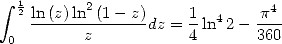 | (435) |
Puis avec
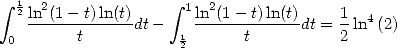 | (436) |
obtenue par intégration par parties et changement de variables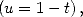 car
car 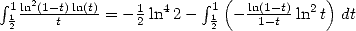 .
.
On a
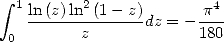 | (437) |
qui donne
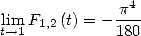 | (438) |
Enfin, en partant de
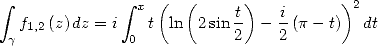 | (439) |
que l’on développe comme dans l’exemple précédent, on trouve
Avec 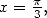 et compte tenu de la valeur de
et compte tenu de la valeur de 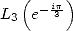
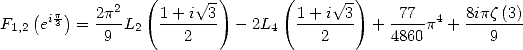 | (440) |
ce qui donne
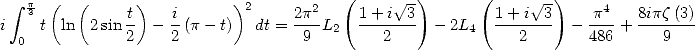 | (441) |
En développant le carré sous l’intégrale et en tenant compte des valeurs précédemment calculées de 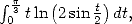 il s’avère (Oh
miracle) que l’on obtient
il s’avère (Oh
miracle) que l’on obtient
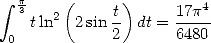 | (Comtet) |
Cette dernière égalité, donne avec 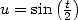 et le DSE de
et le DSE de 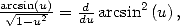 l’égalité
l’égalité
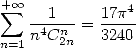 | (442) |
Avec 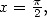 le résultat est moins simple, cependant, on a
le résultat est moins simple, cependant, on a
En combinant avec 433, on a
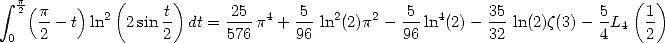 | (444) |
_
Le tout est maintenant de se servir de cette approche pour développer une méthodologie particulière et comme souvent il faut passer par des intégrales équivalentes, dont on vient de voir un premier exemple. Le tout sur une idée de Gery Huvent :
11.4.2 Calcul d’une primitive de 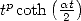
Pour 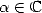 , on introduit la fonction
, on introduit la fonction
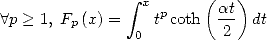 | (445) |
Proposition 23
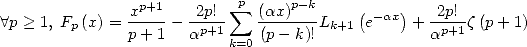 | (446) |
L’égalité précédente est valable sur 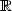 si
si 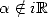
Si 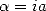 où
où 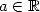 l’égalité précédente est valable sur
l’égalité précédente est valable sur ![] p p [
- a,a.](../mathematiciens/huvent/hyperg1253x.gif)
Preuve. On dérive le membre de droite,
Puis en 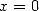 le membre de droite est égal à
le membre de droite est égal à  . _
. _
Application :Intégrales genre Dirichlet
Considérons l’égalité (446) avec 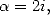 on obtient l’expression de l’intégrale
on obtient l’expression de l’intégrale 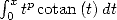 à l’aide de polylogarithmes. Une
intégration par partie (où l’on intégre la cotangente) donne
à l’aide de polylogarithmes. Une
intégration par partie (où l’on intégre la cotangente) donne
On obtient alors les égalités suivantes
Avec 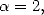 on obtient
on obtient
ce qui donne
Pour le folklore mathématique On montre alors facilement que
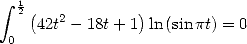 | (459) |
Le minimum du trinôme 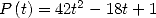 est obtenu en
est obtenu en 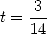 , amusant !
, amusant !
11.4.3 Utilisation de 
Utilisation de la primitive de 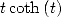 On a pour
On a pour 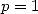 et
et 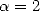
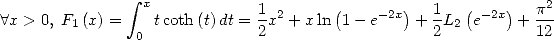 | (460) |
Ainsi pour 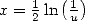 où
où ![u (- ]0,1[,](../mathematiciens/huvent/hyperg1273x.gif) on obtient
on obtient
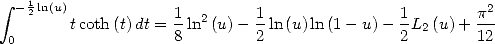 | (461) |
Partant de
![integral x sum oo n n
A x (- [0,1], arcsinhy-dy = -(--1)-C2n-x2n+1
0 y n=022n(2n+ 1)2](../mathematiciens/huvent/hyperg1275x.gif) | (462) |
Le changement de variable 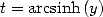 donne alors
donne alors
Comme application, on obtient pour 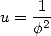
Comme autre application, 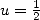 donne
donne
Utilisation de la primitive de 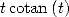 On a pour
On a pour 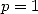 et
et 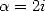
![] [ integral x 2 ( ) ( ) 2
A x (- - p, p , tcotan(t)dt = ix-+ x ln 1 - e- 2ix + i L2 e-2ix - ip--
2 2 0 2 2 12](../mathematiciens/huvent/hyperg1285x.gif) | (466) |
Partant de
![integral x oo sum n
A x (- [0,1], arcsin-ydy = ---C-2n----x2n+1
0 y n=0 22n (2n + 1)2](../mathematiciens/huvent/hyperg1286x.gif) | (467) |
le changement de variable 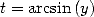 donne
donne
![oo sum ---Cn2n---- 2n+1 iarcsin2x- ( - 2iarcsinx) i ( -2iarcsinx) ip2
A x (- [0,1], 22n (2n + 1)2x = 2 + arcsinx ln 1 - e + 2L2 e - 12
n=0](../mathematiciens/huvent/hyperg1288x.gif) | (468) |
Comme application, on a avec 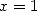
Avec 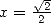
11.4.4 Utilisation de 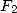
Utilisation de la primitive de 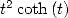 On a pour
On a pour 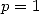 et
et 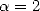
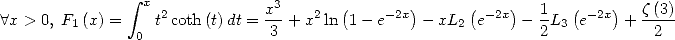 | (471) |
Partant de
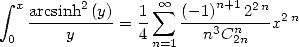 | (472) |
par changement de variable, on obtient ![A x (- [0,1],](../mathematiciens/huvent/hyperg1299x.gif)
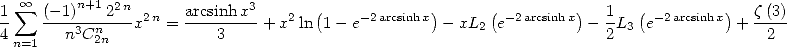 | (473) |
Avec 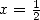 , on obtient
, on obtient
C’est la derniere égalité qu’Apery a utilisé pour prouver l’irrationnalité de 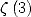 .
.
Avec 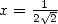 on a
on a
Utilisation de la primitive de  Par le même genre de méthode on obtient
Par le même genre de méthode on obtient
ce qui avec 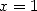 donne
donne
puis avec 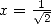
En combinant ces deux dernières égalités avec celle trouvée par Apéry (474), on obtient
11.4.5 D’autres formules
A partir du résultat 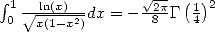 citée dans le Gradshteyn [9] (4.241), on tire la formule
citée dans le Gradshteyn [9] (4.241), on tire la formule
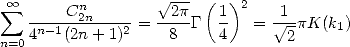 | (484) |
Jolie formule, mettant en évidence l’arrivée d’une constante liée à l’intégrale elliptique de première espèce, pas mal...
Retour à la page d'accueil