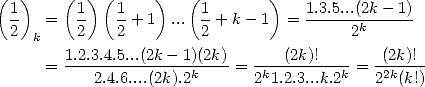|
|
|
|
|
2 Introduction aux séries hypergéométriques
2.1 Définition
Une fonction hypergéométrique généralisée est définie par la série
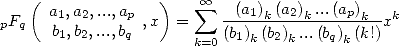 | (1) |
où 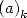 est le symbole de Pochhammer et vaut
est le symbole de Pochhammer et vaut 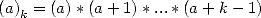
C’est une généralisation de la factorielle. En effet, un exemple simple de valeur du symbole de Pochhammer est 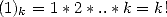
Un exemple très important de valeur du symbole de Pocchammer concerne 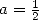 :
:
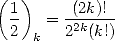 | (2) |
En effet,
qui est équivalent à 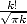 lorsque
lorsque 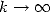 grâce à l’équivalence de Stirling, pour fixer les idées.
grâce à l’équivalence de Stirling, pour fixer les idées.
En effet, on a 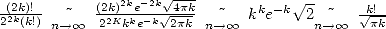 .
.
D’ailleurs, il existe un moyen simple pour vérifier si une série 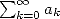 peut se mettre sous la forme d’une série hypergéométrique. On
calcule pour cela le ratio
peut se mettre sous la forme d’une série hypergéométrique. On
calcule pour cela le ratio 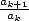 et on tente de le mettre sous la forme
et on tente de le mettre sous la forme
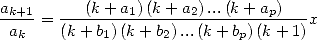 | (4) |
c’est-à-dire un ratio de polynômes en 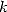 . Sous cette forme, on peut alors préciser que
. Sous cette forme, on peut alors préciser que
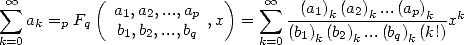 | (5) |
De manière générale, pour les séries n’admettant pas de résultats simples, on pourra souvent se ramener à l’étude d’une intégrale comprenant du logarithme au numérateur (éventuellement à une certaine puissance) et des polynômes (éventuellement à une certaine puissance non entière) soit
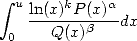 | (6) |
2.2 Quelques propriétés et exemples simples
Le rapport de forces entre 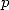 est
est 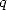 est primordial pour savoir vers quel type de résultat on s’oriente. Car les résultats d’une série
Hypergéométrique pour une différence
est primordial pour savoir vers quel type de résultat on s’oriente. Car les résultats d’une série
Hypergéométrique pour une différence 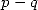 fixée sont ”homogènes”, c’est-à-dire que les fonctions résultant de la série (closed form en
anglais) sont toujours combinaisons d’un même type de fonctions de base. (Bien sûr, les combinaisons peuvent être très compliquées, mais
l’important est que l’on voit toujours apparaitre la même fonction de base)
fixée sont ”homogènes”, c’est-à-dire que les fonctions résultant de la série (closed form en
anglais) sont toujours combinaisons d’un même type de fonctions de base. (Bien sûr, les combinaisons peuvent être très compliquées, mais
l’important est que l’on voit toujours apparaitre la même fonction de base)
Par exemple, l’exemple simple
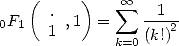 | (7) |
oriente les résultats des séries 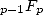 vers les fonctions de Bessel :
vers les fonctions de Bessel :
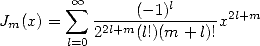 | (8) |
pour la fonction de Bessel de première espèce par exemple (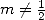 ), tandis que l’autre série
), tandis que l’autre série
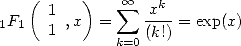 | (9) |
indique que les variations de coefficients pour 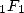 (et plus généralement
(et plus généralement 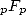 ) fourniront des fonctions basées sur la fonction
exponentielle. Celle-ci, comme on l’a souvent vu, ne se marie pas linéairement avec
) fourniront des fonctions basées sur la fonction
exponentielle. Celle-ci, comme on l’a souvent vu, ne se marie pas linéairement avec 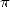 dans le sens où l’on ne trouve guère dans la nature de
série naturelle qui donne par exemple comme résultat
dans le sens où l’on ne trouve guère dans la nature de
série naturelle qui donne par exemple comme résultat 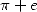 à moins d’ajouter deux séries qui n’ont pas la même forme et qui chacune
converge vers l’une des deux constantes !
à moins d’ajouter deux séries qui n’ont pas la même forme et qui chacune
converge vers l’une des deux constantes !
Je ne connais pas les résultats pour les séries 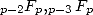 ... mais on voit bien que l’on rajoute alors des factorielles au dénominateur et
l’on a peu de chances de trouver autre chose que des fonctions exotiques impossibles à écrire sous forme de fonctions simples ! Déjà
que la fonction de Bessel... De plus, elles seront plus proches de fonctions vérifiant des propriétés similaires à la fonction
exponentielle.
... mais on voit bien que l’on rajoute alors des factorielles au dénominateur et
l’on a peu de chances de trouver autre chose que des fonctions exotiques impossibles à écrire sous forme de fonctions simples ! Déjà
que la fonction de Bessel... De plus, elles seront plus proches de fonctions vérifiant des propriétés similaires à la fonction
exponentielle.
Remarquons en tous les cas qu’avec les factorielles au dénominateur pour les séries de type 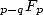 avec
avec 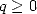 , on a droit
majestueusement à un rayon de convergence infini, c’est sympa.... on le savait déjà pour la fonction exponentielle.
, on a droit
majestueusement à un rayon de convergence infini, c’est sympa.... on le savait déjà pour la fonction exponentielle.
D’autre part, si on prend un coefficient 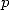 trop grand par rapport à
trop grand par rapport à 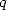 , les séries ont moins d’intérêt calculatoire car ne convergent pas.
Par exemple, la série
, les séries ont moins d’intérêt calculatoire car ne convergent pas.
Par exemple, la série
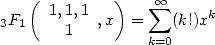 | (10) |
possède un rayon de convergence nul, c’est-à-dire que pour aucun  fixe si petit soit-il on n’arrive à faire converger la série. La
factorielle est trop forte ! Elle croit trop vite par rapport à
fixe si petit soit-il on n’arrive à faire converger la série. La
factorielle est trop forte ! Elle croit trop vite par rapport à 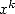 ... C’est donc le cas aussi plus généralement pour les séries
... C’est donc le cas aussi plus généralement pour les séries
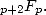
Reste donc un cas intermédiaire représenté par les fonctions 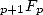 qui ont fourni de nombreux résultats depuis près de deux siècles.
Ceci est dû principalement au fait que ces séries sont homogènes le plus souvent à des combinaisons de radicaux de polynômes genre
qui ont fourni de nombreux résultats depuis près de deux siècles.
Ceci est dû principalement au fait que ces séries sont homogènes le plus souvent à des combinaisons de radicaux de polynômes genre
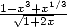 ou des intégrales de ce type de trucs (et en particulier toute la classe des intégrales elliptiques). Et cela c’est bon pour nous, car
on sait qu’avec les intégrales de ce type, l’on rentre de plein pied dans la classe des intégrales qui fournissent des
ou des intégrales de ce type de trucs (et en particulier toute la classe des intégrales elliptiques). Et cela c’est bon pour nous, car
on sait qu’avec les intégrales de ce type, l’on rentre de plein pied dans la classe des intégrales qui fournissent des 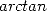 et
et 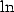 , et donc du
, et donc du
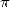 ! !
! !
L’exemple le plus simple est sans doute
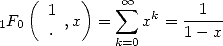 | (11) |
mais on peut aussi s’intéresser à la généralisation du binôme de Newton aux puissances rationnelles et remarquer que
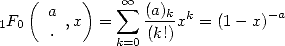 | (12) |
ce qui donne par exemple
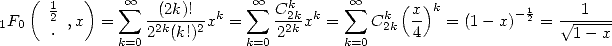 | (13) |
On voit là apparaitre des combinaisons 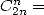
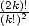 dont les factorielles se prêtent bien à la mise en forme en série hypergéométrique.
Les séries de type
dont les factorielles se prêtent bien à la mise en forme en série hypergéométrique.
Les séries de type 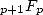 ont un rayon de convergence compris entre l’infini des séries
ont un rayon de convergence compris entre l’infini des séries 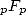 et le zéro des séries
et le zéro des séries 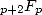 soit tout
naturellement 1 ! On peut s’en convaincre en reprenant le ratio des termes de la série
soit tout
naturellement 1 ! On peut s’en convaincre en reprenant le ratio des termes de la série
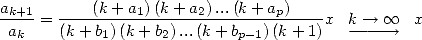 | (14) |
D’après la règle de d’Alembert, la limite de ce ratio est l’inverse du rayon de convergence multiplié par  , donc ici ce rayon vaut
1.
, donc ici ce rayon vaut
1.
La dérivée (et donc la primitive) d’une série hypergéométrique donne encore une série hypergéométrique comme l’illustre par exemple la formule
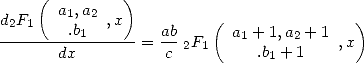 | (15) |
D’ailleurs, les séries hypergéométriques 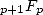 sont solutions d’équations différentielles d’ordre
sont solutions d’équations différentielles d’ordre 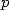 (utilisant la dérivée d’ordre
(utilisant la dérivée d’ordre 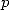 ),
l’exemple ci-dessus en étant une première illustration. Cette propriété rend parfois difficile le calcul de certaines fonctions hypergéométriques,
qui sont équivalentes à des intégrales très pénibles, ou même dont on ne sait pas trop quelle intégrale la représente ! Ces fonctions un peu trop
vastes ont donc rapidement intéressé les mathématiciens qui ont fait preuve d’une grande ingéniosité pour présenter des algorithmes
permettant de calculer indirectement certaines séries hypergéométriques. Une des premières méthodes fut celle de Soeur Céline , puis celui de
Gosper (eh oui, encore lui ! !) et enfin l’aboutissement fut l’algorithme de Wilf-Zeilberger dont la méthodologie, sans être compliquée, est un
peu lourde à expliquer ici...
),
l’exemple ci-dessus en étant une première illustration. Cette propriété rend parfois difficile le calcul de certaines fonctions hypergéométriques,
qui sont équivalentes à des intégrales très pénibles, ou même dont on ne sait pas trop quelle intégrale la représente ! Ces fonctions un peu trop
vastes ont donc rapidement intéressé les mathématiciens qui ont fait preuve d’une grande ingéniosité pour présenter des algorithmes
permettant de calculer indirectement certaines séries hypergéométriques. Une des premières méthodes fut celle de Soeur Céline , puis celui de
Gosper (eh oui, encore lui ! !) et enfin l’aboutissement fut l’algorithme de Wilf-Zeilberger dont la méthodologie, sans être compliquée, est un
peu lourde à expliquer ici...
Vastes les fonctions hypergéométriques, sûrement ! Imaginez-vous que certaines séries bien connues et très simples en sont des cas particuliers. Par exemple, nous avons vu apparaitre dans les formules 12 et 11 des puissances et des combinaisons. Nous pouvons remarquer également qu’une série comme celle de Leibniz-Gregory s’écrit sous la forme d’une série hypergéométrique :
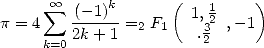 | (Leibniz-Gregory) |
ce qui laisse présager que toutes les séries comprenant exclusivement des termes 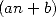 peuvent également s’écrire sous la forme de
séries hypergéométriques avec des paramètres correspondants
peuvent également s’écrire sous la forme de
séries hypergéométriques avec des paramètres correspondants 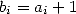 (dans l’exemple ci-dessus,
(dans l’exemple ci-dessus, 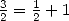 .)
.)
Retour à la page d'accueil