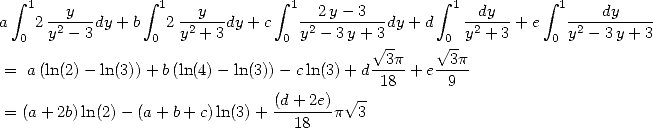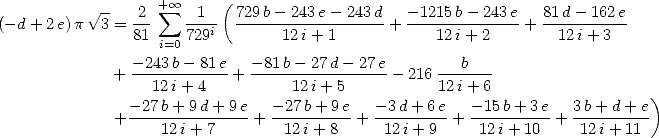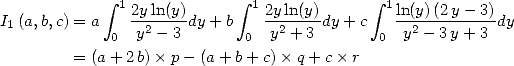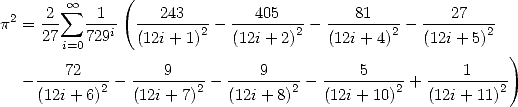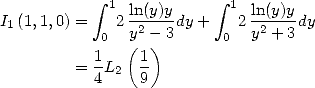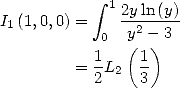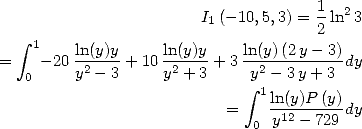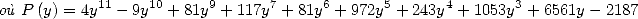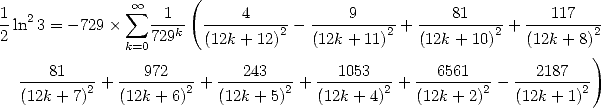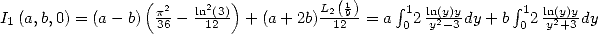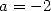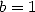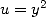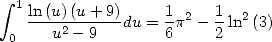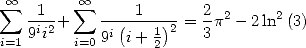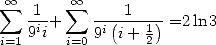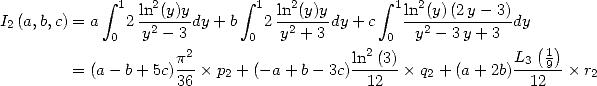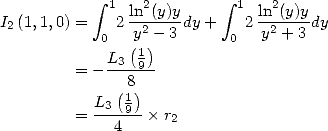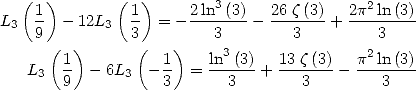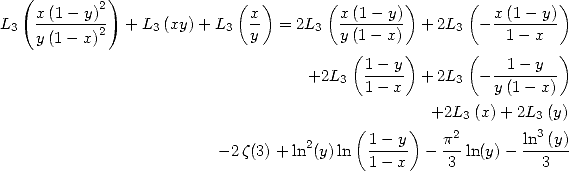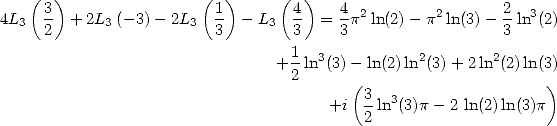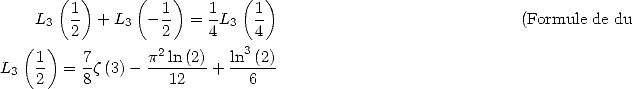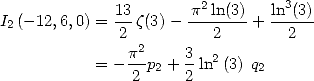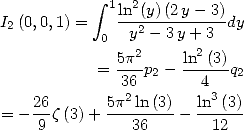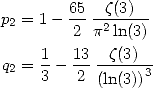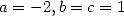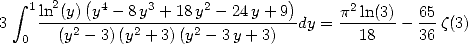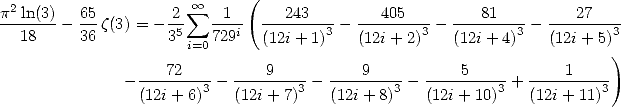 |
|
Historique/Actu (Pi, site, moi)
Edito
Livre
d'or Pages
en .pdf
Je me présente
Quelques photos
Remerciements
Page des nets d'or
Sites qui m'indexent
Derniers changements
Contact |
|
7 
entier fixé,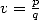
, 
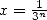: BBP en base 3
Tant de résultats déjà ! Mais ce n’est pas fini... en effet, même si l’on ne peut pas trouver des formules BBP pour toute base, une autre classe
importante de formules BBP a été obtenue pour la base 3, ce qui correspond en fait à prendre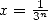 
. Là encore, Gery Huvent a le mieux
expliqué toutes ces relations dans [12].
7.1 Formules pour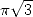 
On reprend le même type d’intégrales que pour la base 2, mais c’est cette fois-ci le 3 qui est omniprésent dans les polynômes.
Un calcul élémentaire montre que
En annulant les coefficients de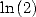 
et 
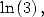on obtient la formule 
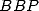pour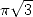 
:
Le cas particulier suivant est le plus élégant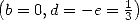 
:
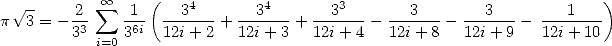 | (Huvent) |
7.2 Formules d’ordre 2 : intégrales avec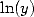 
Il existe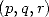 
réels tels que
( les deux membres sont des formes linéaires en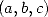 
décomposées sur deux base différentes du dual de 
)
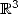Plouffe a montré que
ce qui traduit sous forme intégrale, donne
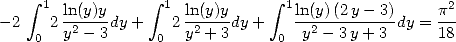 | (271) |
et correspond à l’égalité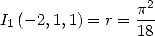 
. On en déduit la valeur de 
.
Or on a
où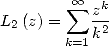 
On en déduit
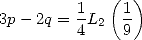 | (273) |
Mais Ramanujan a prouvé que
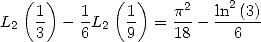 | (274) |
En utilisant
On en déduit
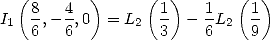 | (276) |
et
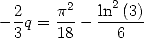 | (277) |
De (273) et (277) on tire les valeurs de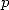 
et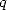 
et l’égalité
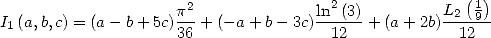 | (278) |
Remarque 7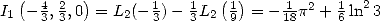 
est une autre relation prouvée par Ramanujan .
7.3 Formules d’ordre 3 : Intégrales avec ln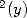
Ici encore, l’ordre 3 introduit des formules donnant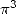 
et autres 
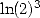mais aussi 
.
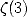Il existe ainsi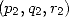 
réels tels que
Le calcul de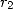 
est élémentaire car
Proposition 11 On a
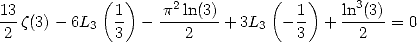 | (285) |
Cette relation est équivalente à
Preuve. L’équation de Kummer pour les polylogarithmes d’ordre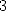 
s’écrit
Avec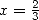 
et 
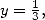on obtient
L’équation de Landen est
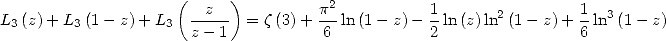 | (290) |
Appliquée 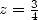à 
et à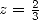 
, elle permet d’exprimer 
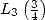et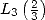 
en fonction de 
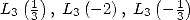et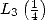 
. La
relation
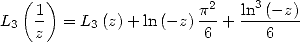 | (291) |
appliquée à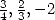 
et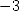 
permet de simplifier le membre de gauche de (289).
Il reste ensuite à utiliser les deux égalités suivantes
pour conclure. _
Avec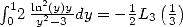 
et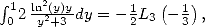 
(285) peut s’écrire
Si on remplace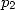 
par sa valeur en fonction de 
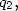le membre de droite de 
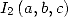devient un polynôme de degré 
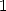en 
dont le
coefficient de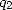 
est égal à 
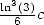. Ainsi 
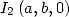ne dépend pas de 
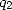. Après calculs, on obtient
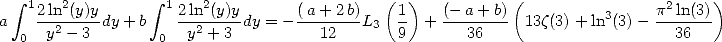 | (294) |
En particulier, on obtient avec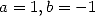 
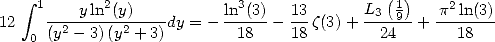 | (295) |
ce qui donne l’égalité
 | (Huvent) |
Remarque 12 On peut aussi prendre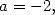 
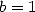et faire le changement de variables 
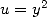qui conduit à
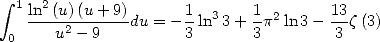 | (296) |
et à la même égalité pour les séries.
Il reste à calculer les valeurs exactes de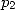 
et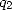 
.
Proposition 13 On a l’égalité
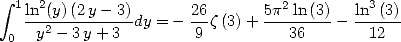 | (297) |
Preuve. L’équation de Landen appliquée à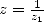 
où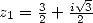 
est une racine de 
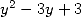(l’autre racine est 
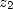telle que
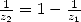) donne
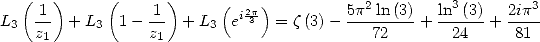 | (298) |
Or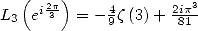 
et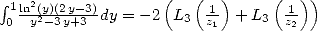 
. On en déduit que
En utilisant les équations (293) et (299), on en déduit que
Et ainsi
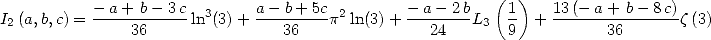 | (302) |
Retour à la page d'accueil