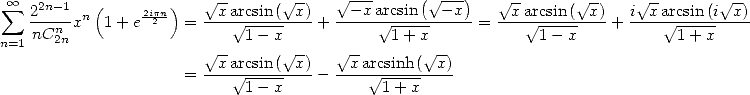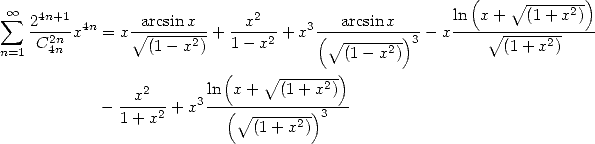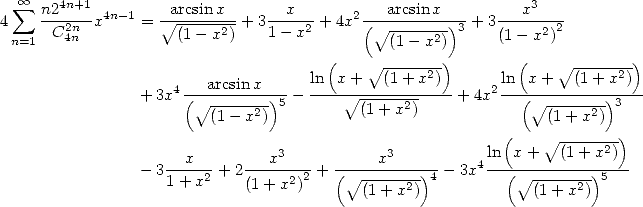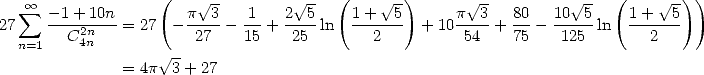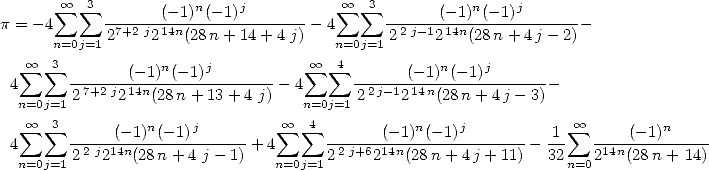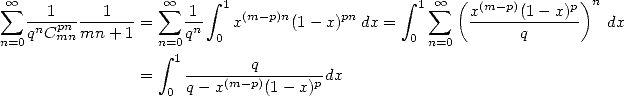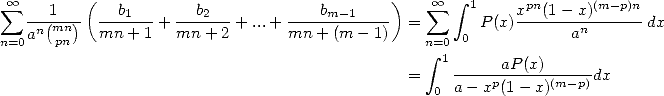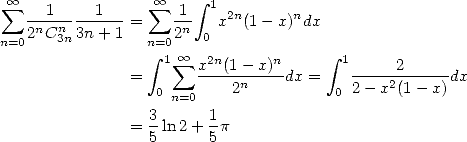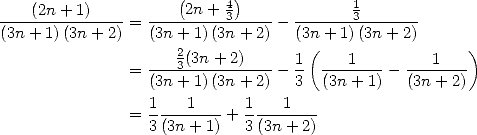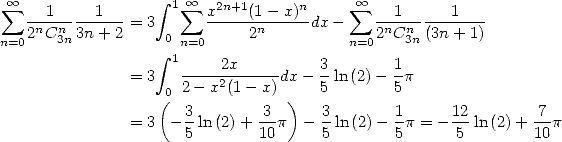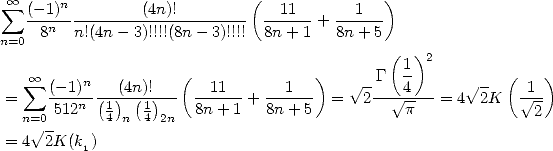|
|
|
|
|
12 Autres coefficients binomiaux
Il n’y a pas que les coefficients binomiaux centraux dans la vie ! On peut également trouver des séries avec d’autres combinaisons au
dénominateur, 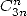 par exemple. Une autre idée est aussi utile : les nombreuses séries avec
par exemple. Une autre idée est aussi utile : les nombreuses séries avec 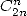 peuvent astucieusement être accélérées en
prenant uniquement une partie des termes de cette série, par exemple en gardant les
peuvent astucieusement être accélérées en
prenant uniquement une partie des termes de cette série, par exemple en gardant les 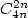 . Voici donc un petit florilège de séries donnant
. Voici donc un petit florilège de séries donnant
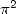 , ou
, ou 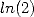 , et qui ne sont sans doute pas toutes connues. Suit la démonstration pour quelques-unes d’entre elles. Certaines sont parmi
les plus rapides des séries rationnelles connues !
, et qui ne sont sans doute pas toutes connues. Suit la démonstration pour quelques-unes d’entre elles. Certaines sont parmi
les plus rapides des séries rationnelles connues !
Sauf mention explicite, ces séries sont des découvertes personnelles, modulo les références que je ne connaitrais pas !
12.1 Formules primitives
Dnas tout ce document, on appellera formule rimitive celle qui minimise le degré des polynômes considérés dans les séries, et qui minimise le
nombre de membres d’une série comme celles des BBP binomiales considérées quelques paragraphes plus bas. En effet, pour une formule
polynomiale binomiale 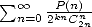 , la décomposition en parties paires et impaires (sommes sur
, la décomposition en parties paires et impaires (sommes sur 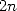 et
et 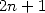 ) fournit une autre série
) fournit une autre série
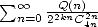 mais qui est pourtant équivalente. Cela dit, peut-être toutes les formules qui suivent ne sont pas primitives, c’est parfois
difficile à voir !
mais qui est pourtant équivalente. Cela dit, peut-être toutes les formules qui suivent ne sont pas primitives, c’est parfois
difficile à voir !
12.2 Formules factorielles polynômiales
En premier lieu, on s’intéresse aux séries de la forme 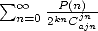 , généralisation des séries
, généralisation des séries 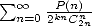 binomiales centrales vues
auparavant.
binomiales centrales vues
auparavant.
- Avec
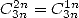 :
:
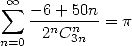 | (485) |
Une telle simplicité, c’est beau...
On a 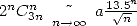 , ce qui permet de conclure que la série précédente apporte un tout petit peu plus d’une décimale par terme,
soit une vitesse d’environ
, ce qui permet de conclure que la série précédente apporte un tout petit peu plus d’une décimale par terme,
soit une vitesse d’environ 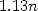 .
.
- Avec
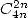 :
:
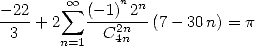 | (Guillera) |
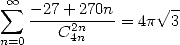 | (486) |
dont je donne deux démonstrations après toutes les formules.
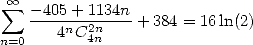 | (487) |
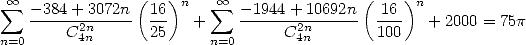
cette dernière forme n’étant pas anodine... nous le verrons dans la partie 12.4. [lien].
Notons que 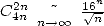 ce qui n’est pas inintéressant d’un point de vue calcul ! Mais attendez de voir la suite...
ce qui n’est pas inintéressant d’un point de vue calcul ! Mais attendez de voir la suite...
Je rappelle ici que si je mets 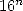 , cela signifie que l’on gagne déjà plus d’une décimale par itération. Le calcul exact se fait en passant au
logarithme décimal (car c’est la réciproque de la fonction
, cela signifie que l’on gagne déjà plus d’une décimale par itération. Le calcul exact se fait en passant au
logarithme décimal (car c’est la réciproque de la fonction 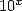 donc cela nous donne
donc cela nous donne  le nombre de décimales, en base
10, équivalentes au nombre entré). Ici,
le nombre de décimales, en base
10, équivalentes au nombre entré). Ici, 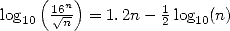 et le
et le 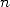 est très grand devant
est très grand devant 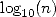 assez
rapidement.
assez
rapidement.
- Avec
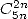
Je n’ai rien trouvé.... ce qui ne veut pas dire qu’il n’existe rien !
- Avec
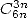 :
:
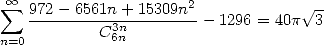 | (488) |
Notons que 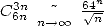
- Avec
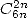 :
:
La dernière formule est parmi celles à faire apparaitre un 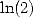 mais pas de
mais pas de 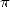 pour la même puissance au dénominateur...
pour la même puissance au dénominateur...
Notons que 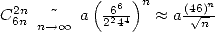 .
.
- Avec
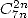 :
:
C’est l’ordre de la relation de Bellard . C’est un ordre un peu particulier, parce que  est un nombre impair ( !). Numériquement, c’est le
seul ordre
est un nombre impair ( !). Numériquement, c’est le
seul ordre 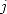 (enfin je crois) pour lequel on trouve un coefficient
(enfin je crois) pour lequel on trouve un coefficient 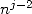 impliqué.
impliqué.
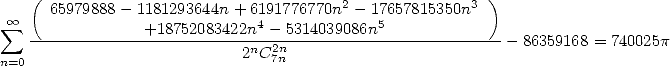 | (492) |
mais aussi
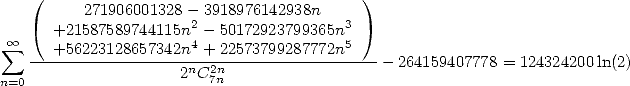 | (493) |
En ce qui concerne la vitesse de convergence, on a 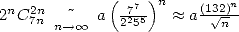
- Avec
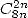 :
:
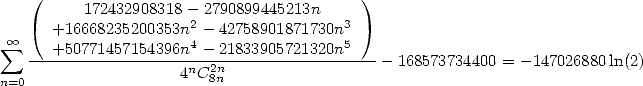 | (494) |
Avec 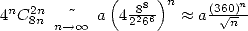
- Avec
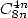 :
:
On a 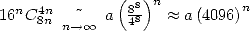
- Avec
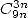 :
:
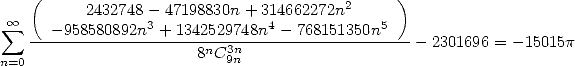 | (497) |
Cette fois, on a 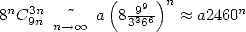
- Avec
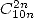 :
:
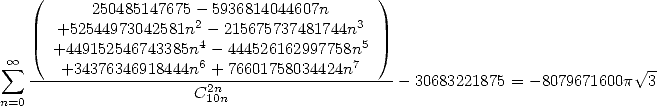 | (498) |
Au niveau des équivalences, on a 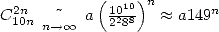
- Avec
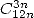 :
:
 | (499) |
Avec 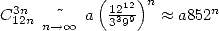
- Avec
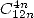 :
:
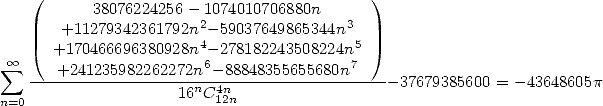 | (500) |
 | (501) |
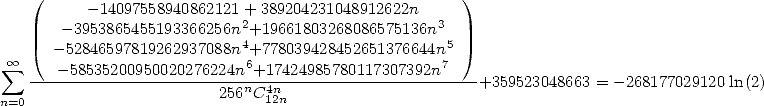 | (502) |
la vitesse est de 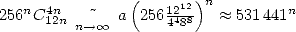
- Avec
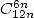 :
:
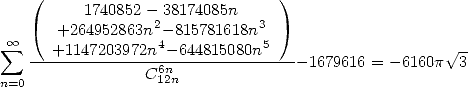 | (503) |
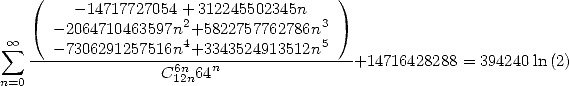 | (504) |
la vitesse est de 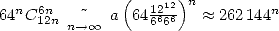 :
:
- Avec
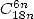 :
:
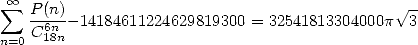 | (505) |
avec 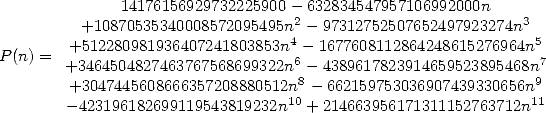
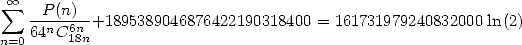 | (506) |
avec 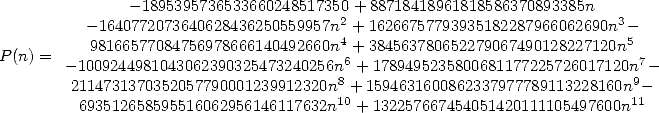
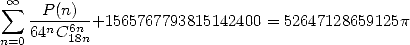 | (507) |
avec 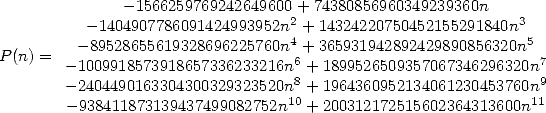
On notera au passage que 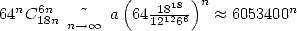 ! ! La dernière formule ajoute un peu plus de 6 décimales nouvelles à
chaque itération ! C’est maintenant meilleur que la meilleure des séries rationnelles de Ramanujan !
! ! La dernière formule ajoute un peu plus de 6 décimales nouvelles à
chaque itération ! C’est maintenant meilleur que la meilleure des séries rationnelles de Ramanujan !
- Avec
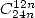 :
:
 | (508) |
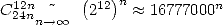 . Impossible hélas de trouver une formule pour
. Impossible hélas de trouver une formule pour 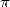 .
.
- Avec
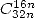 :
:
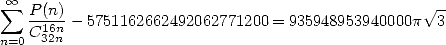 | (509) |
où 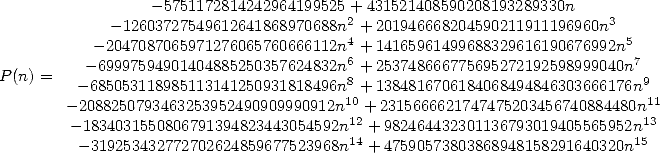
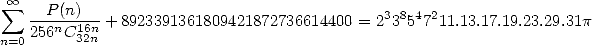 | (510) |
où 
mais aussi
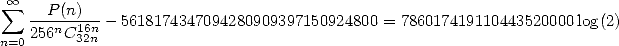
où 
Et si l’on regarde la rapidité de convergence, on obtient
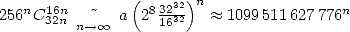 ce qui assure 12 décimales nouvelles à chaque pas de la série !
ce qui assure 12 décimales nouvelles à chaque pas de la série !
Malgré sa complexité apparente, c’est une série rationnelle, donc simple à mettre en oeuvre. Le calcul des coefficients binomiaux centraux peut en outre s’effectuer de manière récursive d’un pas sur l’autre.
- Avec
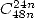 :
:
où 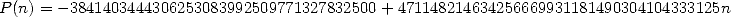
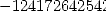

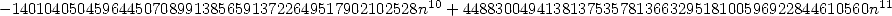
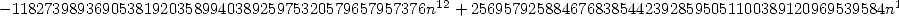
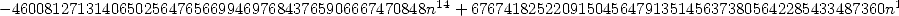
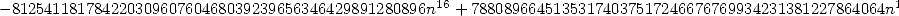
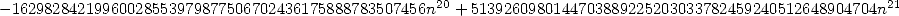
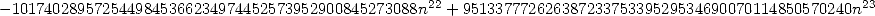
12.3 Alors, que dire de tout cela ?
Plusieurs remarques s’imposent :
- Les gros coefficients devant les constantes se factorisent en produit de nombres premiers assez simples en général, mais cela n’apporte guère d’information sur la nature des coefficients... Ceux à l’intérieur des parenthèses contiennent par contre de gros facteurs premiers.
Exemple : Devant le coefficient de 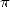 de la dernière série (dénominateur de la fraction devant la série), on a
de la dernière série (dénominateur de la fraction devant la série), on a
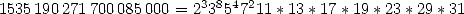 alors que le premier coefficient de la parenthèse se factorise
comme suit :
alors que le premier coefficient de la parenthèse se factorise
comme suit : 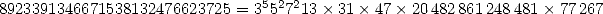 (ce qui est nettement moins
simple !).
(ce qui est nettement moins
simple !).
- En second lieu, on peut déjà noter qu’à chaque ordre où il existe des relations avec
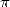 et le logarithme, on trouve des séries
de somme nulle comme pour les séries BBP. Je pense qu’elles le sont en fait ”mécaniquement” et il doit exister un polynôme
et le logarithme, on trouve des séries
de somme nulle comme pour les séries BBP. Je pense qu’elles le sont en fait ”mécaniquement” et il doit exister un polynôme
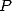 de degré au moins
de degré au moins 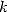 qui annule
qui annule 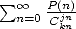 . Mais je n’en ai pas la preuve.
. Mais je n’en ai pas la preuve.
- Ensuite, il semble que seules des constantes bien déterminées soient représentables sous cette forme. Pour ma part, avec
ce genre d’explorations, je n’ai jamais trouvé autre chose que
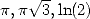 . Pas de
. Pas de 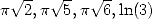 ou
ou 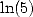 à
l’horizon... je veux bien pour
à
l’horizon... je veux bien pour 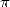 , mais pour les logarithmes c’est tout de même étonnant !
, mais pour les logarithmes c’est tout de même étonnant !
- On peut remarquer également que la répartition des signes est si régulière (surtout dans cette présentation deux par deux
dans la parenthèse !) pour donner une constante, qui a priori n’a pas d’existence plus justifiée qu’une autre... à moins que
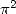 ou
ou 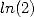 , ce soit vraiment du morceau... En outre, entre les formules pour
, ce soit vraiment du morceau... En outre, entre les formules pour 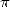 et les formules pour
et les formules pour 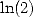 , les coefficients
sont de même ordre et même signe.
, les coefficients
sont de même ordre et même signe.
- Les coefficients également sont remarquables. Ils sont croissants selon les puissances, jusqu’à un certain point, puis sont
décroissants par la suite, comme si ils avaient atteint un maximum. Ce phénomène est particulièrement visible avec la
présentation de la série en
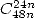 où l’on peut observer que le coefficient maximal survient devant
où l’on peut observer que le coefficient maximal survient devant 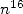 (et comme par hasard,
une puissance de
(et comme par hasard,
une puissance de  et le tiers de 48 !).
et le tiers de 48 !).
- On peut remarquer enfin que hormis le cas
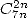 , on a en général des formules pour des combinaisons du type
, on a en général des formules pour des combinaisons du type 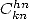 ,
où
,
où 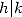 . Et grâce aux propriétés des combinaisons, on sait qu’une formule avec
. Et grâce aux propriétés des combinaisons, on sait qu’une formule avec 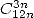 est aussi une formule avec
est aussi une formule avec 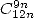 puisque
puisque 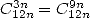 . On peut déjà dresser un petit tableau des formules qui doivent apparaitre naturellement. En effet, on
remarquera qu’entre toutes ces formules, nous avons des traits singuliers qui reviennent. Ainsi, il existe systématiquement des
formules du type
. On peut déjà dresser un petit tableau des formules qui doivent apparaitre naturellement. En effet, on
remarquera qu’entre toutes ces formules, nous avons des traits singuliers qui reviennent. Ainsi, il existe systématiquement des
formules du type 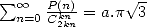 où
où 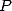 est de degré
est de degré 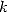 et
et 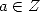 . On a aussi des formules pour
. On a aussi des formules pour 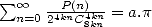 et
et 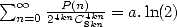 . Ce dernier point est confirmé par l’article [7]. Pour les
. Ce dernier point est confirmé par l’article [7]. Pour les 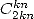 on a souvent des
on a souvent des 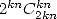 mais
pas toujours (
mais
pas toujours (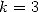 ). Pour les
). Pour les 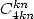 on a toujours des
on a toujours des 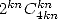 et parfois des
et parfois des 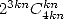 (car
(car 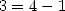 !). Pour les
!). Pour les 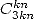 on a des séries avec
on a des séries avec 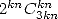 uniquement il me semble. Dans tous ces cas, si il n’y a pas de puissance de
uniquement il me semble. Dans tous ces cas, si il n’y a pas de puissance de  , on tombe sur
une série donnant
, on tombe sur
une série donnant 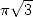 . Si il y a une puissance de 2, on a du
. Si il y a une puissance de 2, on a du 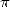 ou du
ou du 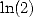 . Facile ! Pour toutes ces formules, avec un
. Facile ! Pour toutes ces formules, avec un 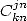 le polynôme
le polynôme 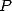 fonction de
fonction de 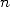 utilisé au numérateur a pour degré au plus
utilisé au numérateur a pour degré au plus 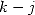 ou plus souvent
ou plus souvent 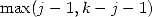 .
.
Remarque 24 Depuis que j’ai écrit ce document, j’ai trouvé un article paru en octobre 2001 [7] qui présente les principes
fondamentaux de recherche de telles formules, et qui montre que l’on peut trouver des séries aussi rapides que l’on souhaite avec
des coefficients binomiaux centraux du type 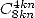 .
.
12.4 Démonstrations
Ces formules semblent difficiles à démontrer car les fonctions qu’elles représentent et donc les éventuelles équations différentielles quelles vérifient ont peu de chance d’être simples...
Les équations différentielles sont sans doute très compliquées, mais on peut ruser un tout petit peu. Remarquons déjà que l’on connait la somme
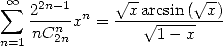 | (513) |
et que la série 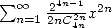 est la composante paire de la précédente série. Ensuite, on a deux méthodes qui peuvent paraitre
naturelles. Une troisième est présentée comme un aboutissement issu de [7].
est la composante paire de la précédente série. Ensuite, on a deux méthodes qui peuvent paraitre
naturelles. Une troisième est présentée comme un aboutissement issu de [7].
- La première consiste à construire des équations différentielles d’après les séries à partir de certaines de leurs propriétés (partie paire d’une autre série...). Ensuite, certains cas particuliers de ces équations différentielles vont fournir des séries :
Intéressons-nous au cas de la série 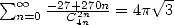 .
.
En premier lieu, on a 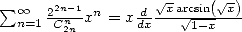 . Il faut donc extraire de la première série 513 une partie de ses membres (ceux
en
. Il faut donc extraire de la première série 513 une partie de ses membres (ceux
en 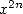 ). On introduit
). On introduit
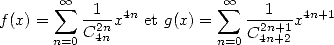 | (514) |
Ce sont, à peu de chose près, les composantes paires et impaires de 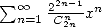 ... plus précisément,
... plus précisément,
Cherchons maintenant une relation entre les fonctions 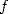 et
et 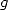 :
:
d’où si l’on dérive la relation 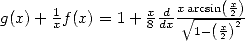 tirée de 515, on obtient
tirée de 515, on obtient
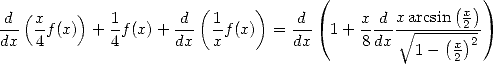 | (518) |
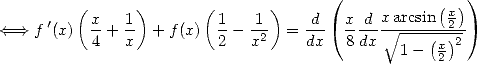 | (519) |
Le membre de droite n’est pas très joli, mais il contient de l’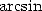 . Il nous suffit maintenant de faire
. Il nous suffit maintenant de faire 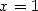 pour trouver
pour trouver
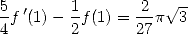 | (520) |
soit
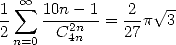 | (521) |
et c’est bien la série cherchée.
On peut aussi prendre  pour trouver
pour trouver
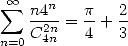 | (522) |
ceci permet également de trouver quasiment les mêmes relations pour 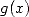 .
.
Enfin, on peut utiliser la fameuse relation 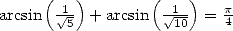 pour obtenir
pour obtenir
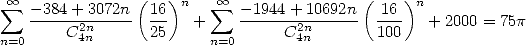 | (523) |
Ce cas marche car on se retrouve avec deux équations pour 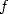 et
et 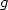 , ce qui permet de s’en sortir par une équation différentielle assez utile.
Si l’on divise de la même manière en trois parties pour trouver par exemple des séries en
, ce qui permet de s’en sortir par une équation différentielle assez utile.
Si l’on divise de la même manière en trois parties pour trouver par exemple des séries en 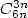 , rien n’est garanti ! D’une manière
générale, les équations différentielles ne seront sans doute pas résolubles, mais on peut s’en servir pour trouver quelques
relations.
, rien n’est garanti ! D’une manière
générale, les équations différentielles ne seront sans doute pas résolubles, mais on peut s’en servir pour trouver quelques
relations.
- L’autre méthode, que m’a soufflé Gery Huvent , consiste à calculer explicitement certains séries qui sont justement des morceaux
d’autres séries, en espérant que des simplifications seront possibles. Pour cela, on utilise le fait que si l’on note
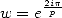 la racine
la racine
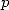 -ième de l’unité, on a
-ième de l’unité, on a 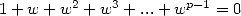 . Donc avec
. Donc avec 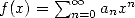
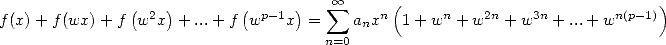
(524)
lorsque 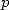 est premier, deux cas se présentent :
est premier, deux cas se présentent : 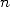 n’est pas multiple de
n’est pas multiple de 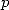 , alors comme les
, alors comme les 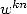 ,
, ![k (- [[0,p- 1]]](../mathematiciens/huvent/hyperg1498x.gif) sont des racines
sont des racines
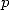 -ièmes de l’unité distinctes,
-ièmes de l’unité distinctes, 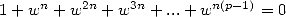 . Si
. Si 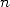 est un multiple de
est un multiple de 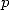 , chaque
, chaque 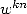 vaut
vaut 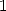 ,
donc
,
donc 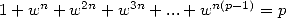 . Avec tout cela, on obtient la somme seulement sur les multiples de
. Avec tout cela, on obtient la somme seulement sur les multiples de 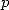 ,
soit
,
soit
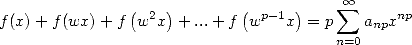 | (525) |
Appliquons tout ceci sans plus tarder ! Mais je ne détaille qu’un seul cas, car tout de même, c’est bien lourd...
Prenons le cas 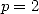 avec la série
avec la série 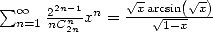 .
.
On obtient d’une part
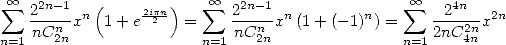 | (526) |
et d’autre part
En rapprochant les deux expressions et en composant par 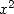 , on obtient l’expression
, on obtient l’expression
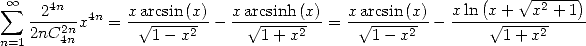 | (528) |

On voit ainsi que l’on ne peut obtenir directement avec cette forme une série donnant 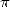 puisque l’on ne peut annuler le terme devant le
logarithme (ou l’on obtient alors une série divergente si l’on avait l’idée de multiplier l’expression par
puisque l’on ne peut annuler le terme devant le
logarithme (ou l’on obtient alors une série divergente si l’on avait l’idée de multiplier l’expression par  et de prendre
et de prendre 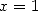 ...). Il
faut dériver la série 528, ce qui donne après multiplication par
...). Il
faut dériver la série 528, ce qui donne après multiplication par  :
:
ce n’est déjà pas très beau... mais en faisant 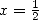 , on obtient
, on obtient
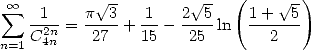 | (530) |
et l’on utilise également une dérivation supplémentaire de manière à faire apparaitre une série en 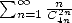 , là c’est carrément
moche !
, là c’est carrément
moche !
en faisant 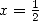 , on obtient
, on obtient
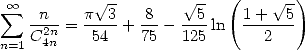 | (532) |
A partir de là, on utilise 530 et 532 pour obtenir
soit
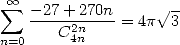 | (534) |
Voilà ! Autant dire que les autres séries en 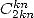 se déduisent de la même manière tandis que la méthode semble plus compliquée à
utiliser par exemple pour les séries en
se déduisent de la même manière tandis que la méthode semble plus compliquée à
utiliser par exemple pour les séries en 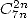 . Si l’on regarde avec un peu de recul les deux méthodes expliquées ci-dessus, on notera que la
première, à base d’équations différentielles, renseigne bien sur la provenance des coefficients des polynômes
. Si l’on regarde avec un peu de recul les deux méthodes expliquées ci-dessus, on notera que la
première, à base d’équations différentielles, renseigne bien sur la provenance des coefficients des polynômes 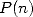 dans
dans
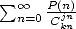 en fournissant directement la formule de formation de ces coefficients au travers de l’équation différentielle.
La seconde permet une plus grande liberté en ce qui concerne les séries produites puisque l’on a l’expression exacte de la
série.
en fournissant directement la formule de formation de ces coefficients au travers de l’équation différentielle.
La seconde permet une plus grande liberté en ce qui concerne les séries produites puisque l’on a l’expression exacte de la
série.
- La méthode présentée maintenant donne une piste de démonstration pour chaque formule ci-dessus. Elle est issue de l’article
[7].
Cette méthode consiste à représenter la combinaison comme une intégrale, puis de sommer et donc d’obtenir une intégrale équivalente à la série, ce qui doit pouvoir se résoudre plus facilement. Explications !
On considère tout d’abord la représentation intégrale de la fonction Bêta, qui fournit aux valeurs entières la formule
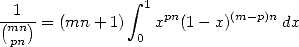
(535) On somme ensuite sur
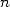 pour obtenir la représentation équivalente de la somme sous forme intégrale
pour obtenir la représentation équivalente de la somme sous forme intégrale
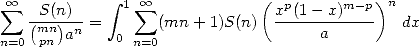
(536) Le polynôme
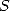 est la clé du problème. Si il est de degré
est la clé du problème. Si il est de degré 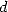 , alors pour obtenir la somme de
, alors pour obtenir la somme de 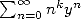 , on dérive successivement
, on dérive successivement
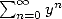 et l’on multiple à chaque fois par
et l’on multiple à chaque fois par 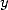 pour compenser le
pour compenser le 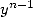 qui apparait avec la dérivation, ce qui permet
d’obtenir
qui apparait avec la dérivation, ce qui permet
d’obtenir
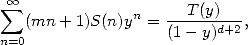
(537) où le polynome
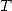 est de degré
est de degré 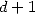 . En écrivant alors que
. En écrivant alors que
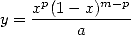
(538) on a finalement
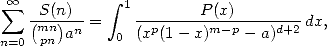
(539) où
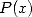 est un polynome en
est un polynome en  de degré
de degré 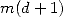 . Les racines du polynome
. Les racines du polynome 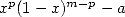 vont être fondamentales en ce qui
concerne l’apparition des constantes. En effet, si
vont être fondamentales en ce qui
concerne l’apparition des constantes. En effet, si 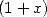 divise ce polynome, on aura du
divise ce polynome, on aura du 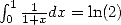 , après décomposition en
éléments simples, qui apparaitra. Si
, après décomposition en
éléments simples, qui apparaitra. Si 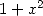 divise
divise 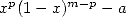 , on aura du
, on aura du 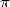 . Les auteurs ne semblent pas considérer de
condition explicite sur les valeurs
. Les auteurs ne semblent pas considérer de
condition explicite sur les valeurs 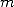 et
et 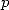 pour voir apparaitre des constantes remarquables, ce que nous ferons, nous, pour les
formules BBP factorielles !
pour voir apparaitre des constantes remarquables, ce que nous ferons, nous, pour les
formules BBP factorielles !
12.5 Combinaisons rapides : Formules factorielles BBP
De la même manière que les 12.2, on peut trouver des formules factorielles ayant la forme de séries BBP. Elles sont tout
aussi rapides ! On s’intéresse donc désormais aux séries de la forme 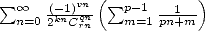 , généralisation des séries
BBP.
, généralisation des séries
BBP.
En voici un petit florilège, parmi lesquelles la démonstration de la formule de Guillera est fournie. On se rendra compte à cette occasion que la méthode ne diffère guère de la deuxième présentée pour les formules factorielles rapides non BBP.
Puis une méthode de démonstration plus générale inspirée des idées de [7] fera l’objet d’une section spéciale !
Notons que peut-être contrairement aux formules factorielles polynomiales, il est ici vraiment fondamental de trouver des séries que l’on
appellera ”primitives” car on peut facilement voir qu’une formule en 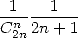 fera éclore mécaniquement une formule en
fera éclore mécaniquement une formule en
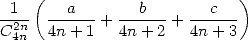 par division de la somme en parties paires (
par division de la somme en parties paires (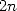 ) et parties impaires (
) et parties impaires (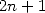 ) puis regroupement des
termes.
) puis regroupement des
termes.
A une formule 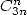 est donc aussi associée une formule en
est donc aussi associée une formule en 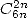 , etc... Mais il n’est pas sûr que j’ai toujours écrit ici uniquement des
formules ”primitives” ! Pas grave, elles sont si belles :-) On est au moins certains que pour une somme
, etc... Mais il n’est pas sûr que j’ai toujours écrit ici uniquement des
formules ”primitives” ! Pas grave, elles sont si belles :-) On est au moins certains que pour une somme 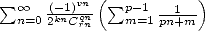 , si
, si
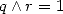 , on a une formule primitive...
, on a une formule primitive...
Un exemple encore pour comprendre cette duperie dans le cas des formules BBP binomiales : pour accélérer artificiellement les séries, on
peut réorganiser les termes de manière à obtenir par exemple 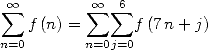 mais cela se voit lorsque l’on factorise les entiers
qui ont alors une facheuse tendance à être assez simples... L’exemple type, c’est ce que m’a fait remarquer Jesus Guillera. La
formule
mais cela se voit lorsque l’on factorise les entiers
qui ont alors une facheuse tendance à être assez simples... L’exemple type, c’est ce que m’a fait remarquer Jesus Guillera. La
formule
qui semble très rapide, est essentiellement réductible à la formule 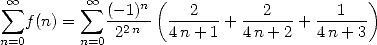 puisque cela
revient à prendre
puisque cela
revient à prendre 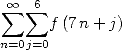 pratiquement. On voit cela au fait que les coefficients entiers utilisés sont très simples (
pratiquement. On voit cela au fait que les coefficients entiers utilisés sont très simples (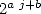 principalement).
principalement).
- Avec
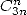 :
:
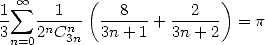 | (Guillera) |
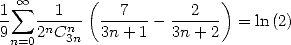 | (541) |
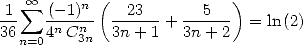 | (Guillera) |
- Avec
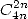 :
:
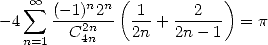 | (Guillera) |
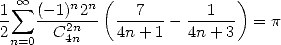 | (Guillera) |
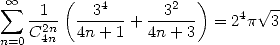 | (542) |
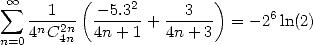 | (543) |
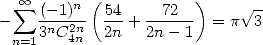 | (Guillera) |
- Avec
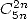 :
:
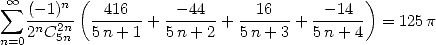 | (Guillera) |
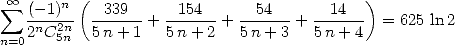 | (Guillera) |
- Avec
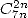 :
:
Tout comme la formule de Bellard, on trouve pour les 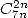 tout plein de sommes très intéressantes
tout plein de sommes très intéressantes
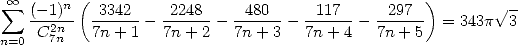 | (544) |
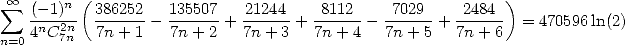 | (545) |
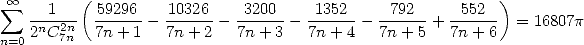 | (546) |
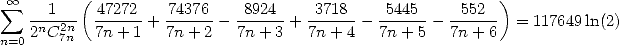 | (547) |
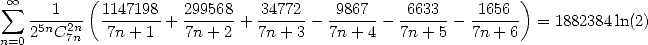 | (548) |
On obtient également comme souvent des représentations de 0, uniquement pour les combinaisons qui donnent lieu par ailleurs à des
valeurs de constantes remarquables ( et
et  ).
).
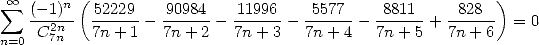 | (549) |
En cherchant du côté des puissances de 3, on trouve également notre bonheur
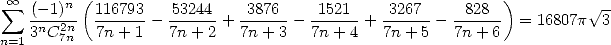 | (550) |
mais à vrai dire, c’est bien tout !
- Avec
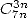
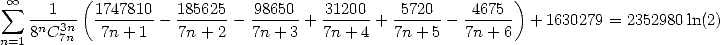 | (551) |
On ne connait pas de formule pour 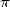 ...
...
- Avec
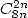 :
:
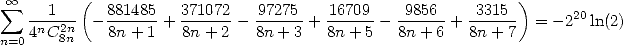 | (552) |
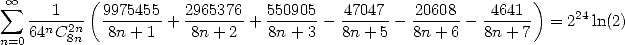 | (553) |
A noter que l’on ne peut apparemment pas trouver là non plus de formule similaire pour 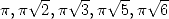 , ce qui semble plutôt
étonnant ! D’autre part, la répartition des signes des membres de la parenthèse ne semble rien avoir d’aléatoire... Serait-ce donc une formule
primitive ? ?
, ce qui semble plutôt
étonnant ! D’autre part, la répartition des signes des membres de la parenthèse ne semble rien avoir d’aléatoire... Serait-ce donc une formule
primitive ? ?
- Avec
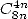 :
:
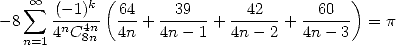 | (Guillera) |
Jesús Guillera a fourni cette jolie et très simple formule en novembre 2001 mais elle n’est pas vraiment une formule primaire mais est
plutôt issue d’une formule en 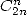 .
.
- Avec
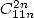 :
:
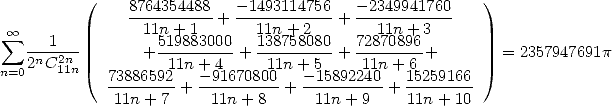 | (Guillera) |
- Avec
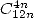 :
:
Les formules qui suivent ne sont probablement plus des formules primitives mais bon.... c’est tout de même joli :-)
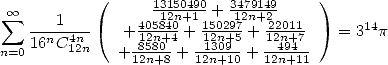 | (554) |
Vous aurez remarqué que 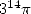 , ça c’est vraiment joli !
, ça c’est vraiment joli !
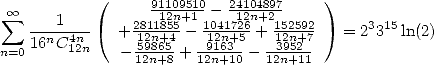 | (555) |
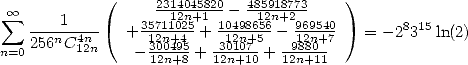 | (556) |
la vitesse est de 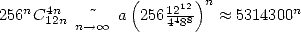
- Avec
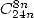 :
:
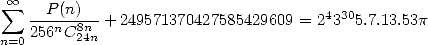 | (557) |
où 
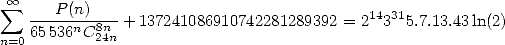 | (558) |
où 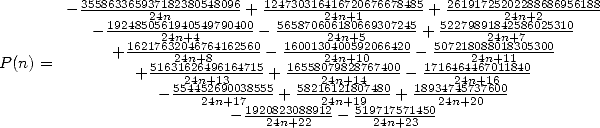
On peut même trouver une fonction 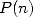 du même type avec
du même type avec 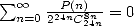 , ce qui représente bien la manière la plus rapide
depuis longtemps de calculer 0 ! !
, ce qui représente bien la manière la plus rapide
depuis longtemps de calculer 0 ! !
- Avec
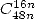 :
:

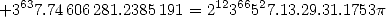
Si c’est pas beau, cela.... admirez la décroissance parfaitement régulière des coefficients entiers....
En ce qui concerne la vitesse, on a 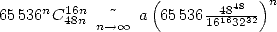 :
: 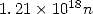 soit donc 18 décimales nouvelles par itération,
sympa ! Mais évidemment, plus de termes sont à calculer donc l’un dans l’autre...
soit donc 18 décimales nouvelles par itération,
sympa ! Mais évidemment, plus de termes sont à calculer donc l’un dans l’autre...
12.6 Alors, que dire de tout cela ?
Cette fois encore, quelques remarques :
- Les gros coefficients devant les constantes se factorisent en produit de nombres premiers assez simples en général, mais cela n’apporte guère d’information structurelle sur la série...
- Les coefficients entiers sur les
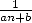 se factorisent mais pas toujours avec des puissances de 2 par exemple. Cela hélas n’apporte
pas vraiment d’indication quant au fait que la série découle ou non d’un découpage facile d’une série d’un ordre inférieur.
se factorisent mais pas toujours avec des puissances de 2 par exemple. Cela hélas n’apporte
pas vraiment d’indication quant au fait que la série découle ou non d’un découpage facile d’une série d’un ordre inférieur.
- Un des inconvénients de ces formules est de devoir utiliser
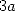 termes en
termes en 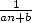 lorsque l’on a affaire à un coefficient
lorsque l’on a affaire à un coefficient 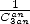 dans la série. Pour les séries polynomiales, on avait plutôt
dans la série. Pour les séries polynomiales, on avait plutôt  termes dans ce cas...
termes dans ce cas...
- Et les ordres supérieurs ? C’est-à-dire les constantes
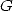 ,
, 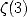 etc... ? les séries du genre [lien vers ma formule cube] utilisent
des coefficients binomiaux centraux, mais avec d’autres coefficients binomiaux ? eh bien bizarrement on ne trouve pas vraiment
de formule BBP au sens habituel, avec plein de termes
etc... ? les séries du genre [lien vers ma formule cube] utilisent
des coefficients binomiaux centraux, mais avec d’autres coefficients binomiaux ? eh bien bizarrement on ne trouve pas vraiment
de formule BBP au sens habituel, avec plein de termes 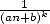 . Pas d’explications à ce phénomène si ce n’est la complexité
des intégrales mises en jeu, qui ne donne pas de constante remarquable, mais ce n’est pas très satisfaisant... Il faudrait étudier
en détail les diviseurs des polynômes au dénominateur des formules. Quelques éléments tout de même un peu plus bas.
. Pas d’explications à ce phénomène si ce n’est la complexité
des intégrales mises en jeu, qui ne donne pas de constante remarquable, mais ce n’est pas très satisfaisant... Il faudrait étudier
en détail les diviseurs des polynômes au dénominateur des formules. Quelques éléments tout de même un peu plus bas.
- On peut se demander à la vue des séries un peu équivalentes polynomiales et BBP (on en trouve pour les mêmes valeurs
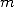 des coefficients
des coefficients 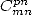 ) si il existe des formules ”canoniques”, des formules de bases, les plus simples possibles au sens de
l’écriture factorielle. En effet, on pourra remarquer que les séries BBP se mettent sous la forme polynomiale si on le veut bien
) si il existe des formules ”canoniques”, des formules de bases, les plus simples possibles au sens de
l’écriture factorielle. En effet, on pourra remarquer que les séries BBP se mettent sous la forme polynomiale si on le veut bien
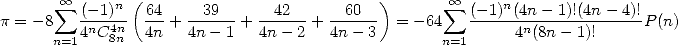
avec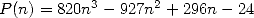 . Mais bien sûr, on voit là que l’on ne peut plus mettre les factorielles sous la
forme d’une combinaison. Ce n’est pas purement notationnel, les combinaisons ont un vrai sens et une cohérence dans le
développement en série entière comme le montre la formule du binome de Newton.
. Mais bien sûr, on voit là que l’on ne peut plus mettre les factorielles sous la
forme d’une combinaison. Ce n’est pas purement notationnel, les combinaisons ont un vrai sens et une cohérence dans le
développement en série entière comme le montre la formule du binome de Newton.
En fait, les représentations intégrales montrent que souvent la forme BBP est plus naturelle et simple que la forme polynômiale, mais ce n’est qu’une remarque intuitive, il manque encore une clarification de l’évaluation de la complexité d’une de ces séries par rapport aux autres.
12.7 Démonstration typique
Jesús Guillera et moi-même proposons ici une méthode de démonstration de ces formules (ne comportant pas de terme
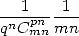 ), destinée à montrer l’existence d’une preuve de ce type pour chaque formule, suivie d’une application à la
première formule de la section. Cette méthode est inspirée de celle de [7], en tentant d’aller un tout petit peu plus loin dans le
détail...
), destinée à montrer l’existence d’une preuve de ce type pour chaque formule, suivie d’une application à la
première formule de la section. Cette méthode est inspirée de celle de [7], en tentant d’aller un tout petit peu plus loin dans le
détail...
12.7.1 La méthode
La série se présente sous la forme
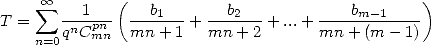 | (559) |
Chouette...
On utilise la représentation intégrale d’une fonction Beta pour obtenir directement que
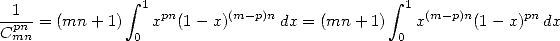 | (560) |
ce qui nous fournit la somme
dont on peut se sortir par une décomposition du dénominateur en éléments simples (attention, je n’ai pas dit que c’était facile ! :-) ).
Bien, mais que fait-on pour les 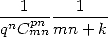 ,
, 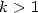 ? ?
? ?
Pour un 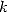 fixé, la décomposition en éléments simples de
fixé, la décomposition en éléments simples de 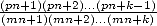 vu comme une fraction rationnelle en n donne une
séquence
vu comme une fraction rationnelle en n donne une
séquence 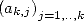 telle que
telle que
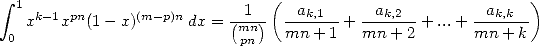 | (562) |
avec 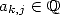 . Pour toutes les valeurs
. Pour toutes les valeurs 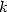 de
de 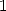 à
à 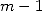 , on dispose donc de séquences
, on dispose donc de séquences 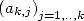 que l’on peut combiner linéairement
pour former les coefficients
que l’on peut combiner linéairement
pour former les coefficients 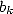 de la somme
de la somme 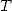 . C’est équivalent à écrire et résoudre le système
. C’est équivalent à écrire et résoudre le système
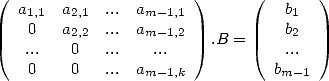 | (563) |
Le vecteur B contient les coefficients de la combinaison linéaire des intégrales contenant 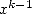 , ce qui fournit le polynôme
, ce qui fournit le polynôme
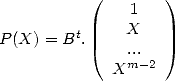 de degré
de degré 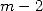 tel que
tel que
Voilà, ce n’est pas plus difficile que cela !
On peut aussi, dans un souci de construction des formules et non plus de preuve, choisir un polynome 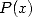 qui simplifie volontairement
certains diviseurs au dénominateur de l’intégrale équivalente. On se retrouve alors dans une situation dont on parle plus longuement
12.7.4.
qui simplifie volontairement
certains diviseurs au dénominateur de l’intégrale équivalente. On se retrouve alors dans une situation dont on parle plus longuement
12.7.4.
12.7.2 Application : La démo de la première formule
On reprend la première formule Guillera
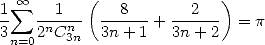 | (565) |
On utilise la formule intégrale

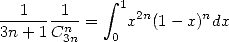 | (566) |
qui se montre par récurrence par exemple pour les puristes ! On en déduit que
Pour 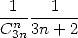 , c’est un peu plus compliqué, mais on peut s’en sortir quand même en suivant la méthode de la section ci-dessus, à
savoir que
, c’est un peu plus compliqué, mais on peut s’en sortir quand même en suivant la méthode de la section ci-dessus, à
savoir que
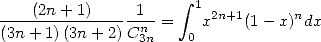 | (568) |
On a
donc
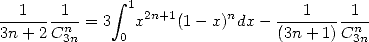 | (571) |
ce qui est équivalent à considérer que le fameux polynôme à chercher est 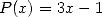 car on a
car on a
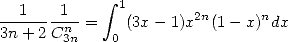 | (572) |
comme le polynôme est simple, on a pu le déterminer explicitement, mais ce ne sera pas toujours le cas (voir démo plus bas).
Le calcul est maintenant direct
donc finalement en reprenant la méthode de la 6.2de Gery Huvent , on a
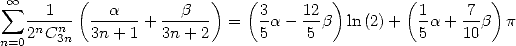 | (574) |
 On choisit maintenant
On choisit maintenant 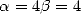 pour annuler la participation de notre cher
pour annuler la participation de notre cher 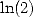 et obtenir Guillera. On peut également prendre
et obtenir Guillera. On peut également prendre
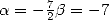 pour obtenir 541.
pour obtenir 541.
12.7.3 Démo de la formule en 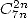
Jesus Guillera et moi-même proposons maintenant une preuve rapide d’une des plus belles formules du lot, à savoir 546.
On rappelle que le principe consiste à chercher le polynôme 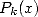 tel que
tel que
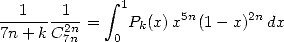
Bien que la solution, pour chaque k, ne soit pas unique, on sait que le degré de 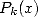 est
est 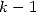 . Par la méthode du système linéaire,
on obtient
. Par la méthode du système linéaire,
on obtient

Maintenant, on déroule....
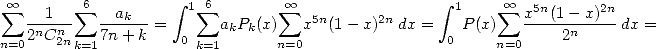
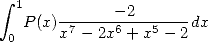
Avec les 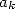 de la formule 546, on a
de la formule 546, on a 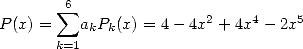
et
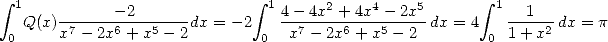 | (575) |
Incroyable, non ? ? Que cette si grosse somme soit en fait équivalente à une intégrale aussi simple, c’est assez génial !
12.7.4 Prédiction des formules
A la vue de la démonstration, on peut se demander si il existe un moyen de prévoir pour quelles combinaisons il existe une formule. Je n’ai pour l’instant pas de réponse exhaustive, mais une condition suffisante est déjà assez simple à exhiber.
On a vu en effet avec la formule en 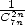 que l’intégrale était équivalente à
que l’intégrale était équivalente à 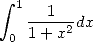 . Cela provient du fait que
. Cela provient du fait que
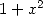 divise
divise 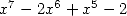 et le polynôme au numérateur (donc les coefficients) sert donc uniquement à simplifier
l’autre facteur. Or pour les formules non alternées, le polynôme du dénominateur est engendré par
et le polynôme au numérateur (donc les coefficients) sert donc uniquement à simplifier
l’autre facteur. Or pour les formules non alternées, le polynôme du dénominateur est engendré par 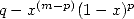 que l’on appellera un polynome générateur. A partir de là, une condition suffisante d’existence d’une formule pour
que l’on appellera un polynome générateur. A partir de là, une condition suffisante d’existence d’une formule pour 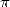 est
que
est
que
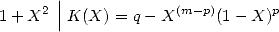
Donc il faut que 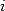 et
et 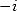 soient racines de
soient racines de 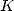 . En particulier, on a pour
. En particulier, on a pour 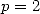 ,
, 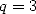 ,
, 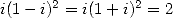 .
Ceci prouve l’existence d’une formule en
.
Ceci prouve l’existence d’une formule en 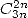 pour
pour 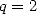 . Mais comme
. Mais comme 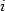 et
et 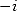 sont racines 4-ième de
sont racines 4-ième de 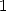 , on peut
multiplier
, on peut
multiplier 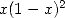 par
par 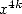 sans changer l’existence des racines
sans changer l’existence des racines 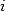 et
et 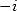 . Ceci prouve alors l’existence d’une formule en
. Ceci prouve alors l’existence d’une formule en
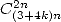 .
.
Tentons de préciser la condition suffisante :
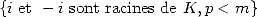
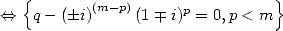
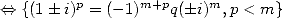
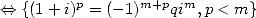 par conjugaison
par conjugaison
![{ }
<==> ( V~ 2)p = q et pp =_ (m + p)p+ m p [2p],p < m
4 2](../mathematiciens/huvent/hyperg1714x.gif) par passage en module et argument
par passage en module et argument
![{ p } { k }
<==> 22 = q, p < m et - p =_ 2m [8] <==> p = 2k, 2 = q, p < m et 7p =_ 2m[8]](../mathematiciens/huvent/hyperg1715x.gif)
Les choses sont claires. Pour que l’on puisse obtenir une formule BBP factorielle non alternée grâce à l’intégrale 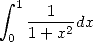 , il faut et
il suffit que
, il faut et
il suffit que 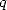 soit une puissance de
soit une puissance de  ,
, 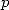 pair plus petit que
pair plus petit que 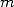 et surtout la superbe relation de congruence
et surtout la superbe relation de congruence ![7p =_ 2m [8]](../mathematiciens/huvent/hyperg1721x.gif) . On vérifiera
aisément que les conditions
. On vérifiera
aisément que les conditions 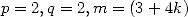 vérifient ces conditions. On trouve aussi que la condition est vérifiée pour
vérifient ces conditions. On trouve aussi que la condition est vérifiée pour
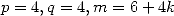 , formules que j’avais manqué dans mes expérimentations ! Comme quoi, parfois la théorie va plus vite que la
pratique... :-)
, formules que j’avais manqué dans mes expérimentations ! Comme quoi, parfois la théorie va plus vite que la
pratique... :-)
En appliquant la même méthode aux séries alternées, aux racines 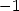 (qui permettent de trouver du
(qui permettent de trouver du 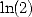 grâce à
grâce à 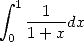 ), au
polynôme
), au
polynôme 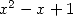 (pour trouver du
(pour trouver du 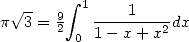 ), on trouve les conditions suivantes, et donc les formules
suivantes :
), on trouve les conditions suivantes, et donc les formules
suivantes :
Pour les séries non alternées 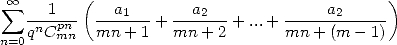
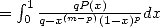
| Pôle | Constante | Condition avec racines | Condition d’existence du pôle 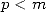 | Type de formule existante |
 | 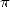 | 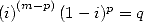 | ![p = 2k, 2k = q,7p =_ 2m [8]](../mathematiciens/huvent/hyperg1735x.gif) | 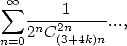 |
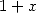 | 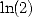 | 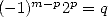 | 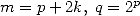 | Un paquet vu la relation ! |
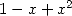 | 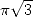 | 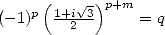 | 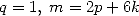 | 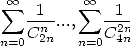 |
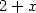 | 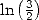 | 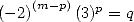 | 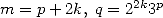 | 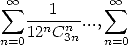 |
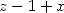 | 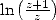 | 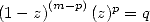 | 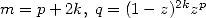 | ... |
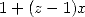 | 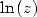 | 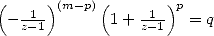 | 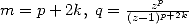 | ... |
Il faut noter que lorsque l’on a besoin qu’une polynome ayant des racines complexes divise notre polynome générateur, on a besoin
seulement que l’une des racines complexes soit racine de ce polynome, par conjugaison (à cause du fait que le polynome
générateur est réel). Ce tableau indique par exemple pourquoi l’on trouve si souvent de formules pour 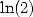 mais pas
toujours pour
mais pas
toujours pour 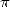 . Bien que l’on ait affaire ici à une condition suffisante et pas nécessaire, les conditions sur les logarithmes
montrent qu’il est probable que l’on ne puisse pas obtenir d’autres logarithmes entiers que
. Bien que l’on ait affaire ici à une condition suffisante et pas nécessaire, les conditions sur les logarithmes
montrent qu’il est probable que l’on ne puisse pas obtenir d’autres logarithmes entiers que 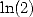 avec des puissances
avec des puissances 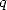 entières.
entières.
Pour les séries alternées 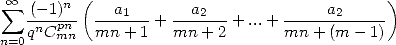
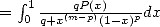
| Pôle | Constante | Condition avec racines | Condition d’existence du pôle 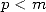 | Type de formule existante |
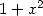 | 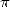 | 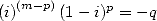 | ![k
p = 2k, 2 = q,7p =_ 2m + 4[8]](../mathematiciens/huvent/hyperg1769x.gif) | 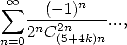 |
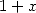 | 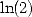 | 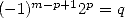 | 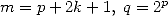 | Un paquet vu la relation ! |
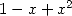 | 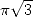 | 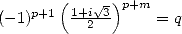 | 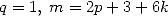 | 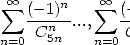 |
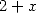 | 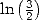 | 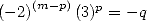 | 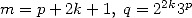 | 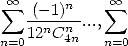 |
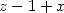 | 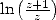 | 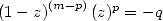 | 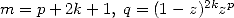 | ... |
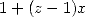 | 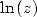 | 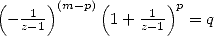 | 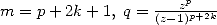 | ... |
12.8 Produit de combinaisons
Une très intéressante question concerne la possible présence de plusieurs combinaisons dans une série donnant 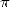 . Je dois
vous avouer que je pensais cela peu probable, jusqu’à la découverte de la formule suivante en décembre 2001, due à Jesús
Guillera
. Je dois
vous avouer que je pensais cela peu probable, jusqu’à la découverte de la formule suivante en décembre 2001, due à Jesús
Guillera
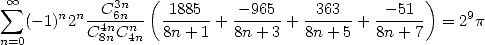 | (Guillera) |
La même avec des factorielles
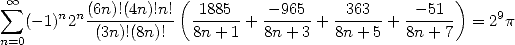 | (Guillera) |
On a aussi
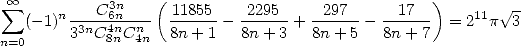 | (Gourevitch) |
soit
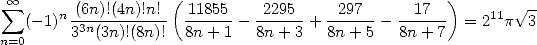 | (Gourevitch) |
Alors, d’où cela vient-il ? Eh bien au lieu de partir de puissances entières dans l’intégrale, on passe par des puissances rationnelles et en particulier des racines carrées. En effet, en considérant l’intégrale
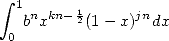 | (576) |
on obtient des sommes de la forme
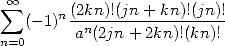 | (577) |
soit par example pour 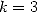 et
et 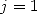
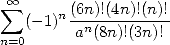 | (578) |
ou encore pour 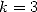 et
et 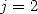
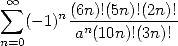 | (579) |
Les sommes BBP se déduisent alors après intégration pour donner des formules du type
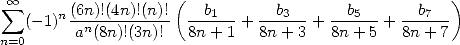 | (580) |
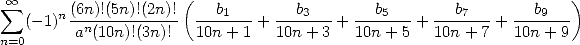 | (581) |
Pour la première formule Guillera, on considère par exemple l’esquisse de preuve suivante
Preuve. 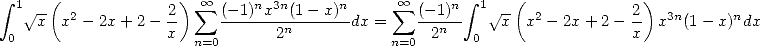
et l’on utilise ensuite les valeurs connues de 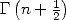 . _
. _
Un autre exemple comprend
où 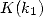 est la fonction elliptique de première espèce en la première valeur singulière, célèbre contante de la théorie
elliptique !
est la fonction elliptique de première espèce en la première valeur singulière, célèbre contante de la théorie
elliptique !
Il est obtenu à partir de
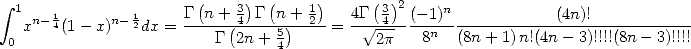 | (583) |
et
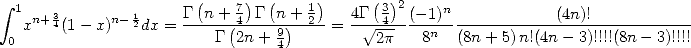 | (584) |
et l’intégrale
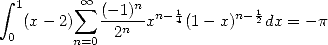 | (585) |
Tout ceci ouvre des perspectives très intéressantes !
Notez également que la forme BBP est une forme très générale des séires dans la mesure où même les formules du genre de celles de Ramanujan peuvent se mettre sous la forme BBP, comme
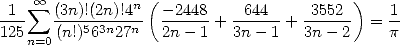 | (586) |
Par contre, hélas, nous n’avons pas encore trouvé de méthode pour prouver ces formules avec la méthode Bêta...
Beaucoup plus de détails et quelques autres formules sont donnés dans l’article [13], disponible prochainement j’espère !
Retour à la page d'accueil