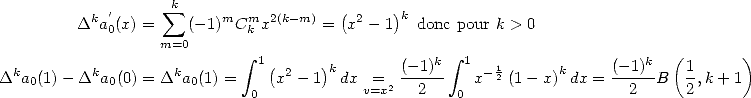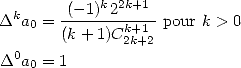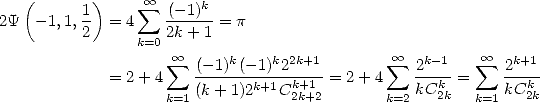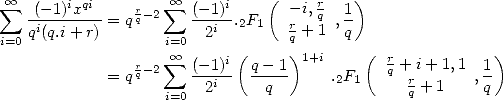10 Introduction de factorielles et combinaisons

Ce qui est très intéressant, c’est que l’on pourra toujours observer le même type de constantes malgré l’introduction d’une combinaison ou de factorielles équivalentes (à condition de rester dans une 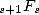), c’est pourquoi 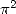et les logarithmes vont représenter l’essentiel des résultats fournis par des hypergéométriques simples. Par contre, dès que l’on introduira une combinaison au carré par exemple, on obtiendra des types différents, des rapports de fonction gamma le plus souvent (et donc aussi  ! 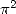mais de manière moins évidente).

10.1 Un premier exemple

L’introduction des combinaisons est justifiée par plusieurs séries très similaires avec ou sans présence de combinaisons. Par exemple,

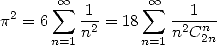(Euler)

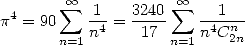(Comtet 1974)

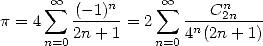(362)

Ce qui signifie en fait que dès que l’on trouve un résultat de cette fonction , on a de petits espoirs de trouver le même type de résultats avec une combinaison de type coefficient binomial central par exemple. Ceci est simplement dû à la forme assez proche des fonctions génératrices de ces séries (1211).

10.2 Umbral calculus

On peut établir un lien entre les séries avec combinaisons (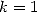 plus précisément) et les séries sans combinaisons (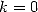) au moyen de l’accélération de la convergence par la méthode d’Euler. Celle-ci est un cas particulier de la formule des ”finite differences” qui est la version discrète du développement de Taylor (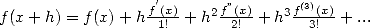). C’est la théorie connue sous le nom de ”Umbral calculus”, dont l’origine remonte à Sylvester (1814-1897). La méthode d’accélération d’Euler consiste à remplacer la somme d’une série par la somme de différences de termes de la série.

Plus précisément, on choisit une série alternée 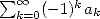et l’on calcule la différence finie d’ordre 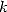pour  :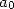

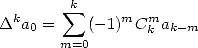(363)

alors

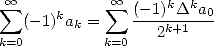(364)

Le truc, c’est que le terme 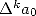va parfois s’écrire comme des combinaisons ou rapports de factorielles et autres symboles de Pochammer ! Application :

On sait que 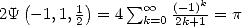. On a donc .

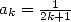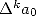étant assez délicat à calculer directement, on pose la fonction

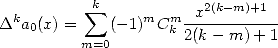(365)

On en cherche la valeur en 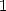bien sûr. Et l’on calcule !

où 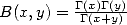est la fonction Bêta complète qui vaut dans ce cas de valeurs de 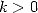entières 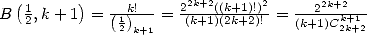(tiens, tiens...).

D’où on obtient

et donc d’après la formule 364

Hélas, je n’ai pas trouvé comment généraliser la méthode... Cependant, on a tout de même la formule plus générale

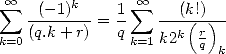(369)

et même

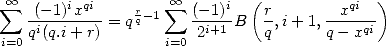(370)

où B est une Bêta incomplète, si je ne me trompe pas...

De même, en utilisant le lien entre bêta incomplètes et hypergéométriques

où 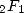est la fonction hypergéométrique.

Bref, l’introduction de factorielles peut se révéler intéressante franchement intéressante...