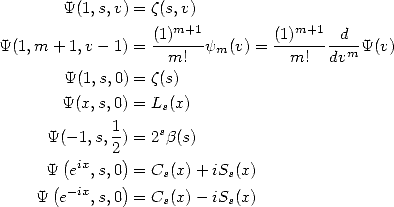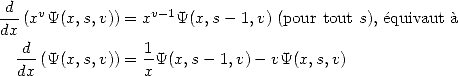3 La fonction Psi : Base des formules type Machin ou BBP

3.1 Définition

On veut pouvoir combiner au sein d’une série 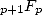les combinaisons et les termes 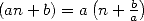. On introduit pour cela la fonction Psi, ou transcendante de Lerch, qui s’écrit

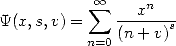(16)

pour 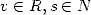. Le rayon de convergence est 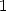. On peut écrire cette fonction sous la forme d’une série hypergéométrique assez simple :

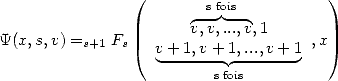(17)

Cette fonction a l’avantage de regrouper une bonne partie des fonctions classiques de l’analyse, et qui ne demandent que cela tant les relations entre elles sont nombreuses !

Ainsi, on a

où 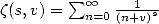est la fonction Zêta de Hurwitz, 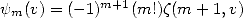est la fonction PolyGamma et 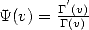est la fonction Digamma.

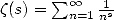est la fameuse fonction Zêta, 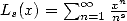est le polylogarithme d’ordre s, 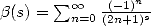est la fonction Bêta de Dirichlet, et enfin 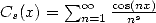et 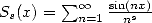sont les fonctions de Clausen.

3.2 Equations différentielles

La fonction 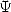est une série hypergéométrique, on peut donc la barder d’équations différentielles en tous genres. Parmi celles-ci, citons :

mais aussi en itérant

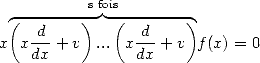(26)