|
The world of Pi - V2.57 modif. 13/04/2013 |
|
|
|
Contents page
1 A quick historical recap
2 Introduction to hypergeometric series
2.1 Definition
2.2 A few properties and simple examples
3 The function Psi : Basis of formulae of kind Machin or BBP
3.1 Definiton
3.2 Differential equations
4 Formula of type Machin
5 BBP formulae: The technic
5.1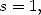
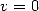 : The polylogarithms
: The polylogarithms
5.1.1 Definition
5.1.2 Remarquable values
5.1.3 Formula of duplication
5.1.4 Euler's and Landen's formulae for the dilogarithm
5.1.5 Landen's formula for the trilogarithm
5.1.6 Particular values
5.1.7 A few classicals integrals
5.2 Links between integrals, BBP formulae and polylogarithm
5.2.1 Notations
5.3 Integrals and BBP formuale
5.3.1 Integrals equivalent to BBP series
5.3.2 More general integrals and BBP formulae
5.3.3 Calculation of integrals
5.4 Function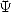 and
polylogarithms
and
polylogarithms
5.5 Interest in BBP formulae
6 BBP formulae in base 2 :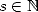 ,
,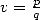 ,
, 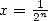 in
in 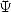
6.1 The considered integrals
6.2 The method
6.3 Formulae for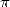 ,
, 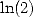 ,
,
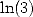 and
and 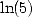
6.3.1 Application to BBP formulae for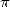
6.3.2 BBP formulae for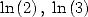 and
and 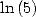
6.4 Cases of polylogarithms of order : Formulae of order 2
: Formulae of order 2
6.4.1 The classicals expressions :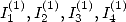 and
and 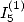
6.4.2 Calculation of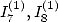 and
and 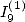
6.4.3 Calculion of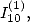 relation between
relation between 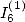 and
and 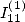
6.4.4 Applications of the determanition of BBP formulae
6.4.5 A few composite formulae
6.5 Cases of polylogarithms of order 3
6.5.1 Calculation of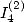
6.5.2 Calculation of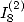
6.5.3 Relationship bewteen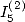 and
and 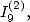 value of
value of 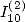
6.5.4 Calculation of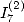
6.5.5 Application to the determinaion of BBP formulae
6.6 Cases of polylogarithms of order 4
6.6.1 The relationship
6.6.2 Application to the determination of BBP formulae
6.6.3 Formulae for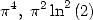 and
and 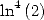
6.7 Case of polylogarithm of order 5
6.7.1 The relationship
6.7.2 Application to the determination of BBP formulae
6.7.3 Formulae for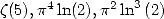 and
and 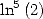
6.7.4 Simplifications of those formulae
7 fixed integres,
fixed integres,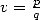 ,
, 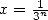 : BBP in base 3
: BBP in base 3
7.1 Formulae for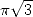
7.2 Formulae of order 2 : Integrals with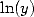
7.3 Formulae of order 3 : Integrals with ln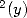
8 And the other bases then ? ?
9 Polygamma and Clausen
9.1 The polygamma function
9.2 The function digamma
9.3 Polygamma of order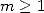
9.3.1 Links between the integrals and the BBP formulae
9.3.2 A graphical approach
9.3.3 Analytical translation
9.4 Combinations by Kölbig
9.4.1 Clausen's functions
9.4.2 Kölbig's results.
10 Introduction to factorials and combinations
10.1 A first example
10.2 Umbral calculus
11 Central binomial series
11.1 Inversion of combinations
11.2 Useful developpments
11.3 First direct formulae
11.4 Formulae of greater order
11.4.1 A first formulae with demo
11.4.2 Calculation of a derivation of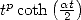
11.4.3 Uses of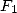
11.4.4 Uses of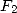
11.4.5 Other formulae
12 Other binomial coefficients
12.1 Primitive formulae
12.2 Polynomials factorial formulae
12.3 So, what does all this mean ?
12.4 Proofs
12.5 Fast combinations: BBP factorial formulae
12.6 So, what does all this mean ?
12.7 Typical proof
12.7.1 The method
12.7.2 Application : The proof of the first formula
12.7.3 Proof of the formulae in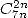
12.7.4 Prediction of formulae
12.8 Product of combinations
13 Harmonics series
13.1 Proximity of harmonic series and of polylogarithms
13.2 Study of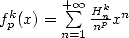 and of
and of
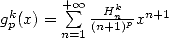
13.2.1 Definitons, remarquable links
13.2.2 Calculation of certain functions
13.3 Applications of calculation of certain series
13.3.1 With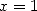
13.3.2 With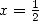
13.3.3 With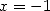
13.3.4 With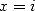
13.3.5 With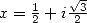
13.3.6 With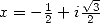
13.3.7 With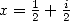
13.4 Generalisations
13.4.1 Euler's sum
13.4.2 A formula combining Harmonic and combination
13.4.3 An other formula
13.4.4 Harmonics of harmonics!
14 Series of greater factorial: Ramanujan, Borwein, Chudnovsky....
14.1 Squared central binomial coefficients: Elliptical formulae
14.2 Cubic central binomial ceofficients: Ramanujan's Identity
15 Other hypergeometric formulae concerning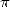
2 Introduction to hypergeometric series
2.1 Definition
2.2 A few properties and simple examples
3 The function Psi : Basis of formulae of kind Machin or BBP
3.1 Definiton
3.2 Differential equations
4 Formula of type Machin
5 BBP formulae: The technic
5.1
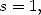
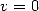 : The polylogarithms
: The polylogarithms
5.1.1 Definition
5.1.2 Remarquable values
5.1.3 Formula of duplication
5.1.4 Euler's and Landen's formulae for the dilogarithm
5.1.5 Landen's formula for the trilogarithm
5.1.6 Particular values
5.1.7 A few classicals integrals
5.2 Links between integrals, BBP formulae and polylogarithm
5.2.1 Notations
5.3 Integrals and BBP formuale
5.3.1 Integrals equivalent to BBP series
5.3.2 More general integrals and BBP formulae
5.3.3 Calculation of integrals
5.4 Function
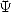 and
polylogarithms
and
polylogarithms
5.5 Interest in BBP formulae
6 BBP formulae in base 2 :
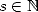 ,
,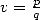 ,
, 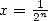 in
in 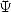
6.1 The considered integrals
6.2 The method
6.3 Formulae for
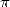 ,
, 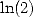 ,
,
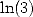 and
and 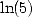
6.3.1 Application to BBP formulae for
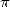
6.3.2 BBP formulae for
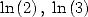 and
and 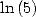
6.4 Cases of polylogarithms of order
 : Formulae of order 2
: Formulae of order 2
6.4.1 The classicals expressions :
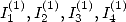 and
and 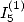
6.4.2 Calculation of
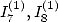 and
and 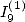
6.4.3 Calculion of
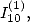 relation between
relation between 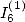 and
and 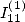
6.4.4 Applications of the determanition of BBP formulae
6.4.5 A few composite formulae
6.5 Cases of polylogarithms of order 3
6.5.1 Calculation of
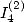
6.5.2 Calculation of
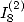
6.5.3 Relationship bewteen
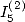 and
and 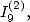 value of
value of 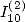
6.5.4 Calculation of
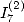
6.5.5 Application to the determinaion of BBP formulae
6.6 Cases of polylogarithms of order 4
6.6.1 The relationship
6.6.2 Application to the determination of BBP formulae
6.6.3 Formulae for
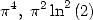 and
and 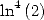
6.7 Case of polylogarithm of order 5
6.7.1 The relationship
6.7.2 Application to the determination of BBP formulae
6.7.3 Formulae for
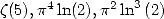 and
and 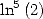
6.7.4 Simplifications of those formulae
7
 fixed integres,
fixed integres,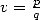 ,
, 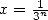 : BBP in base 3
: BBP in base 3
7.1 Formulae for
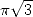
7.2 Formulae of order 2 : Integrals with
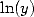
7.3 Formulae of order 3 : Integrals with ln
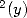
8 And the other bases then ? ?
9 Polygamma and Clausen
9.1 The polygamma function
9.2 The function digamma
9.3 Polygamma of order
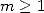
9.3.1 Links between the integrals and the BBP formulae
9.3.2 A graphical approach
9.3.3 Analytical translation
9.4 Combinations by Kölbig
9.4.1 Clausen's functions
9.4.2 Kölbig's results.
10 Introduction to factorials and combinations
10.1 A first example
10.2 Umbral calculus
11 Central binomial series
11.1 Inversion of combinations
11.2 Useful developpments
11.3 First direct formulae
11.4 Formulae of greater order
11.4.1 A first formulae with demo
11.4.2 Calculation of a derivation of
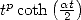
11.4.3 Uses of
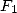
11.4.4 Uses of
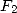
11.4.5 Other formulae
12 Other binomial coefficients
12.1 Primitive formulae
12.2 Polynomials factorial formulae
12.3 So, what does all this mean ?
12.4 Proofs
12.5 Fast combinations: BBP factorial formulae
12.6 So, what does all this mean ?
12.7 Typical proof
12.7.1 The method
12.7.2 Application : The proof of the first formula
12.7.3 Proof of the formulae in
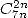
12.7.4 Prediction of formulae
12.8 Product of combinations
13 Harmonics series
13.1 Proximity of harmonic series and of polylogarithms
13.2 Study of
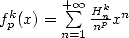 and of
and of
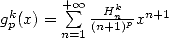
13.2.1 Definitons, remarquable links
13.2.2 Calculation of certain functions
13.3 Applications of calculation of certain series
13.3.1 With
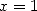
13.3.2 With
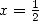
13.3.3 With
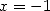
13.3.4 With
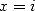
13.3.5 With
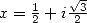
13.3.6 With
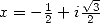
13.3.7 With
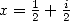
13.4 Generalisations
13.4.1 Euler's sum
13.4.2 A formula combining Harmonic and combination
13.4.3 An other formula
13.4.4 Harmonics of harmonics!
14 Series of greater factorial: Ramanujan, Borwein, Chudnovsky....
14.1 Squared central binomial coefficients: Elliptical formulae
14.2 Cubic central binomial ceofficients: Ramanujan's Identity
15 Other hypergeometric formulae concerning
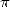
[next page ][top page ][table of contents ]
back to home page
