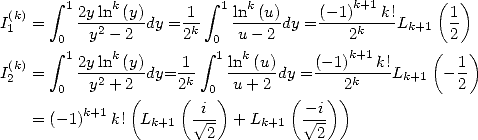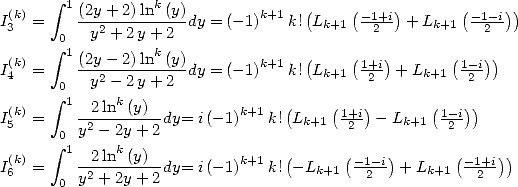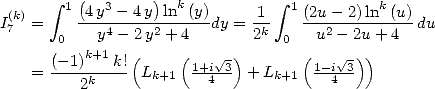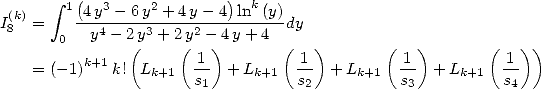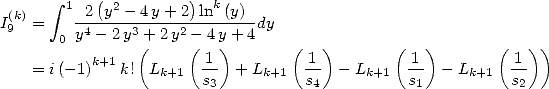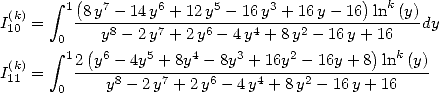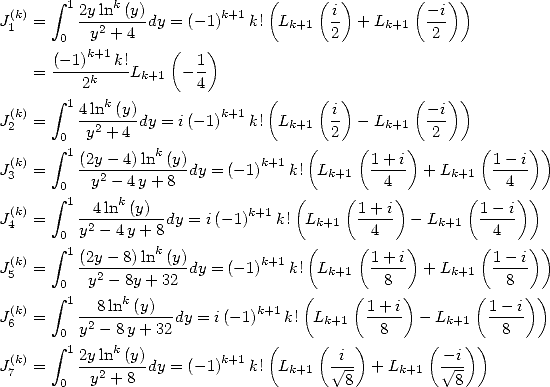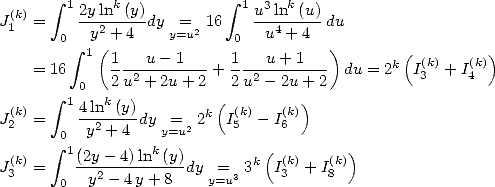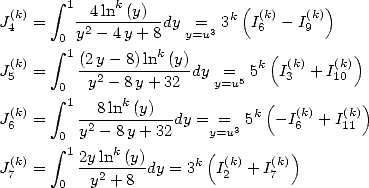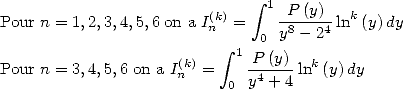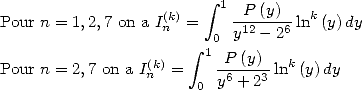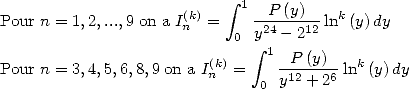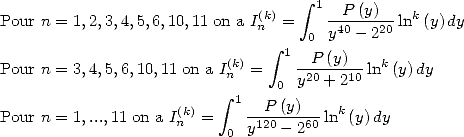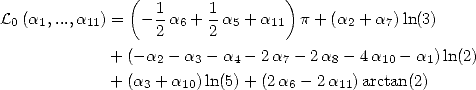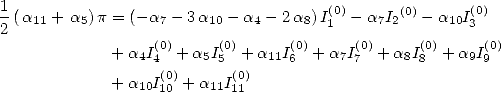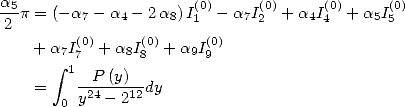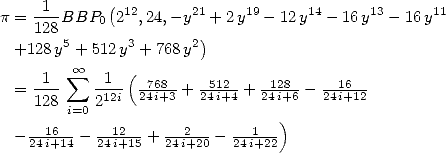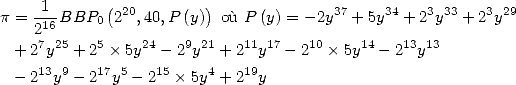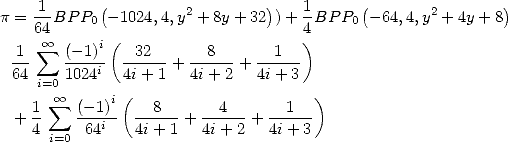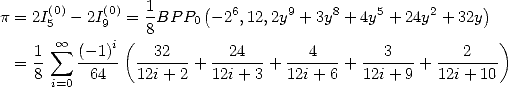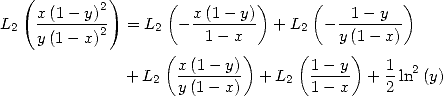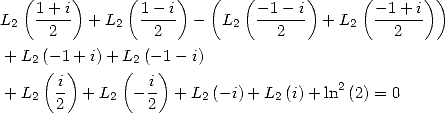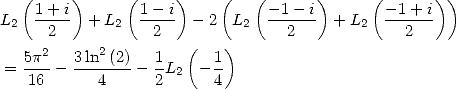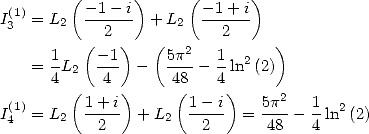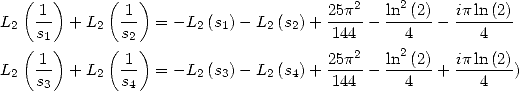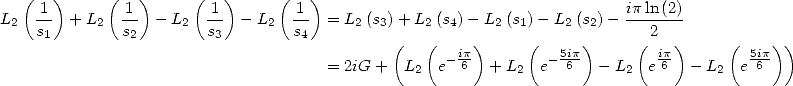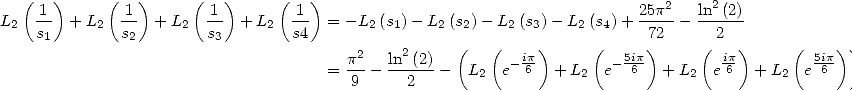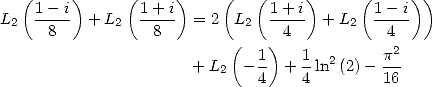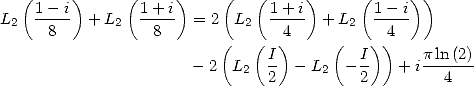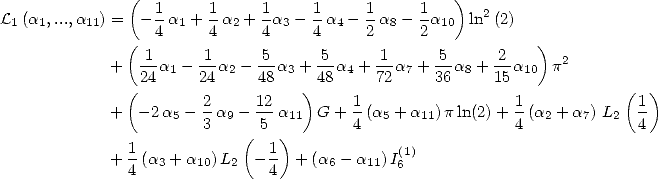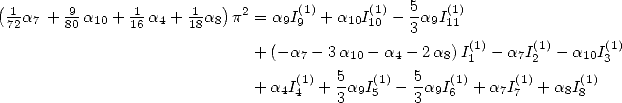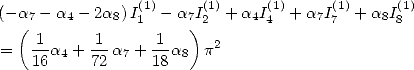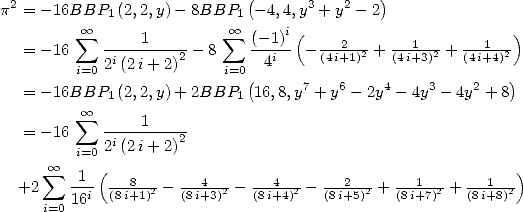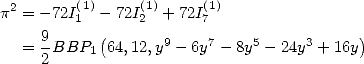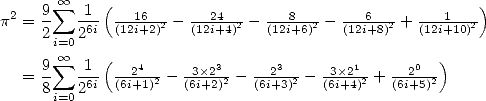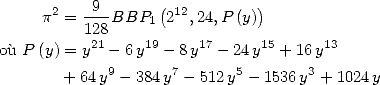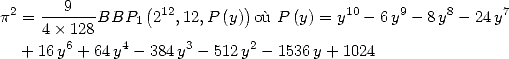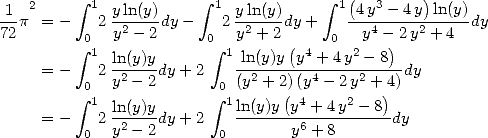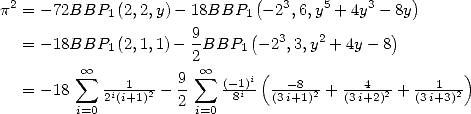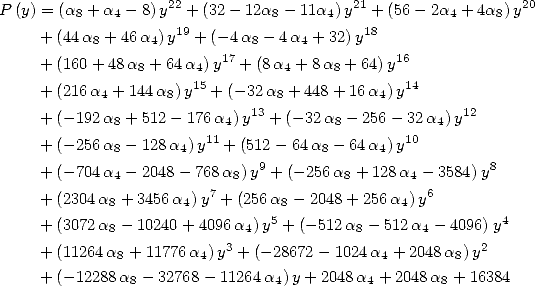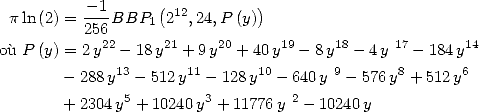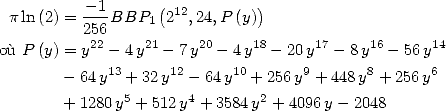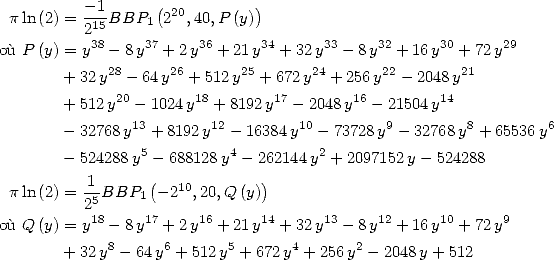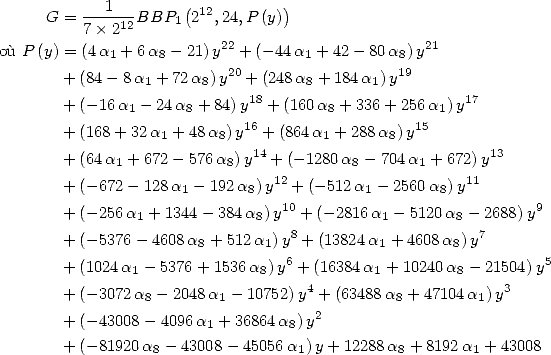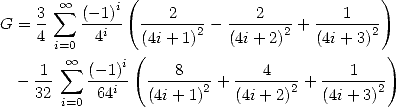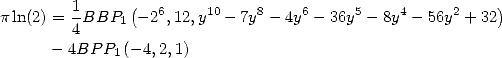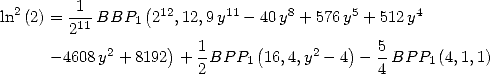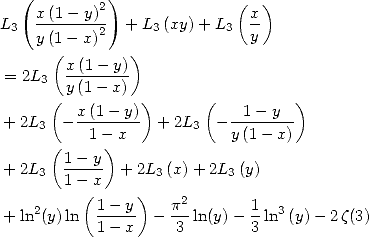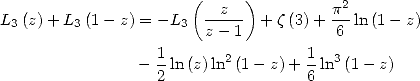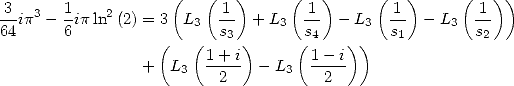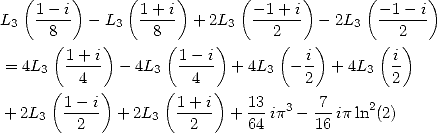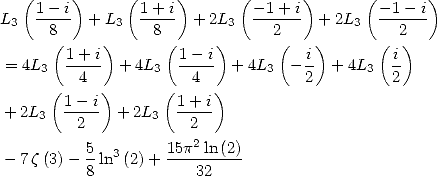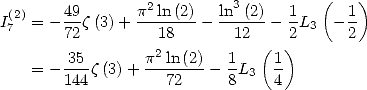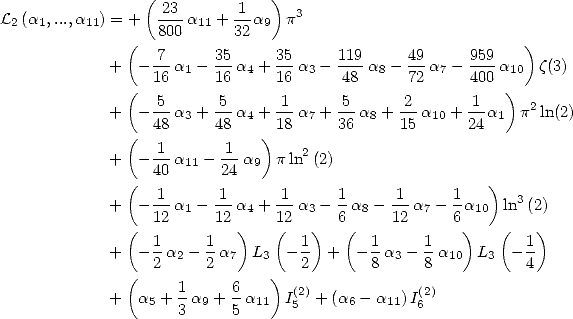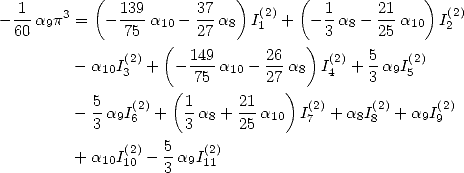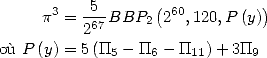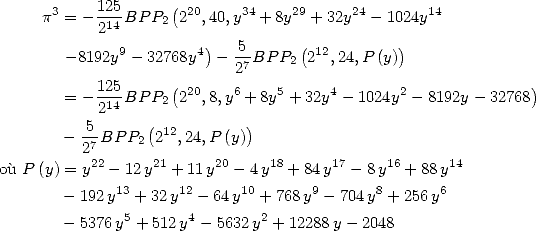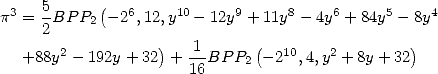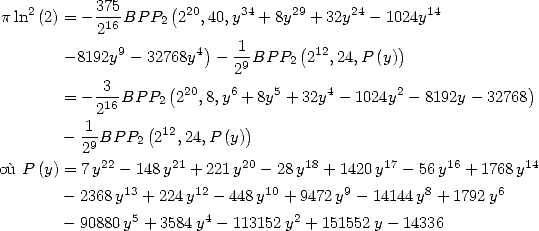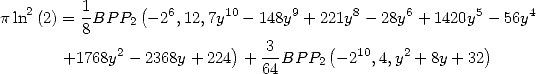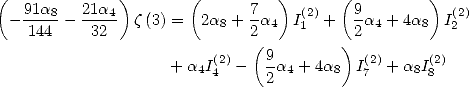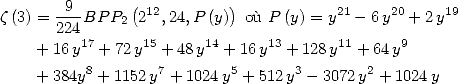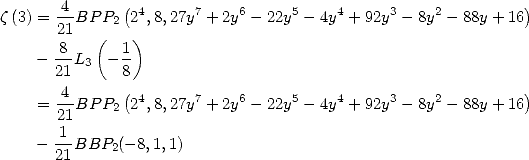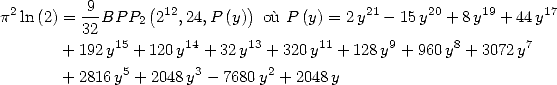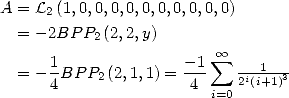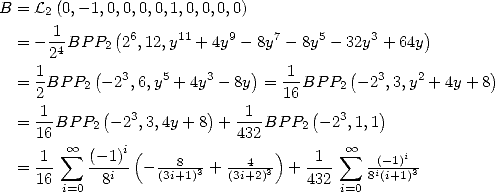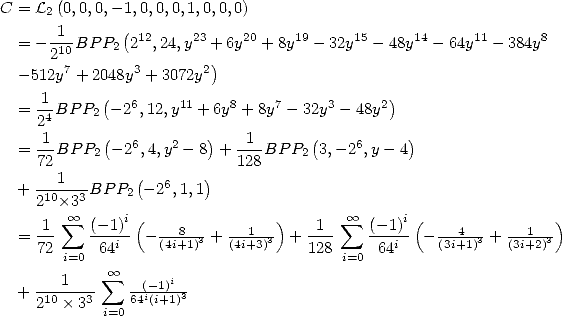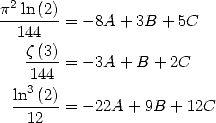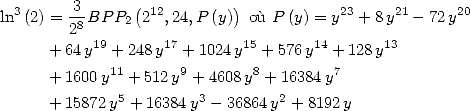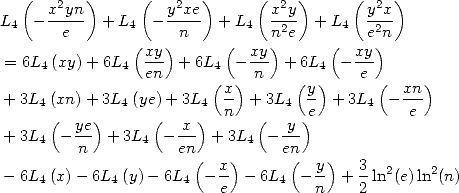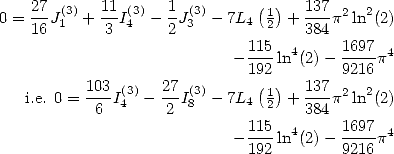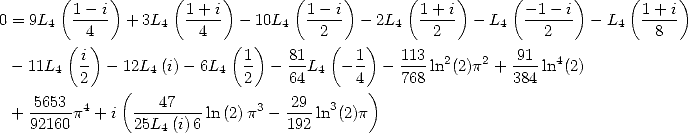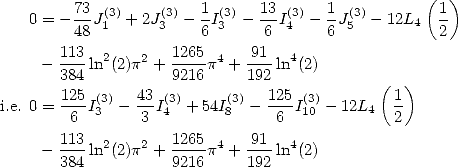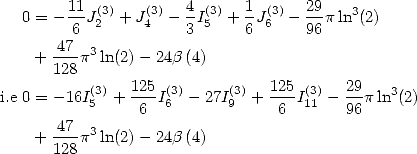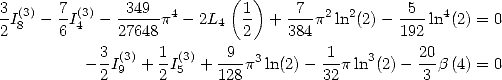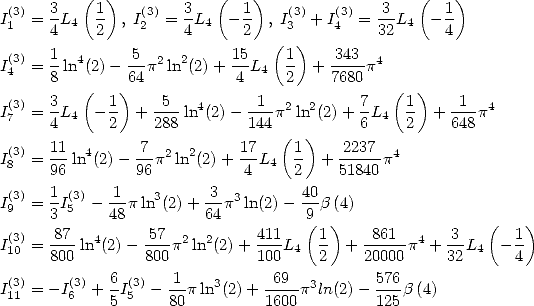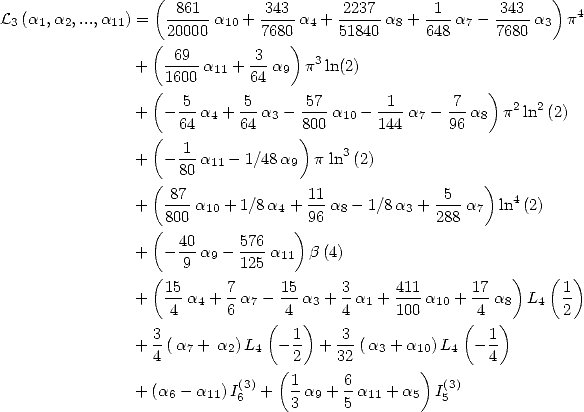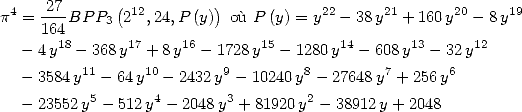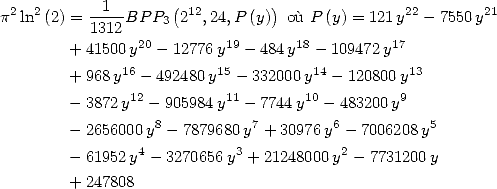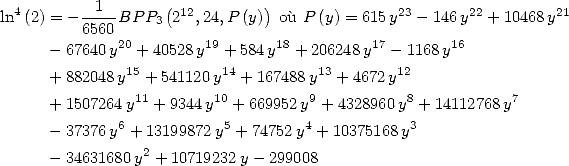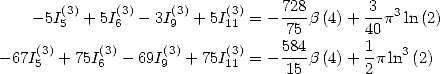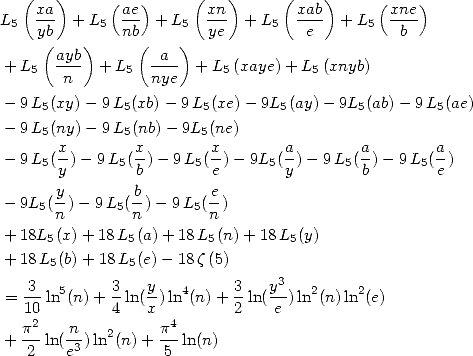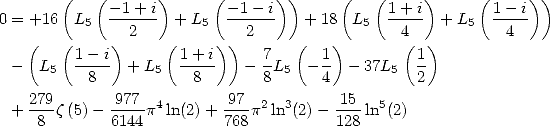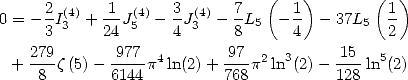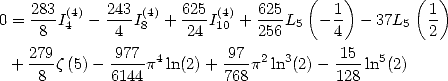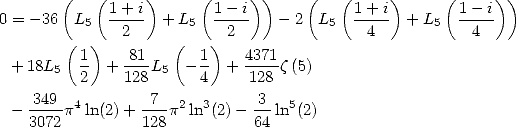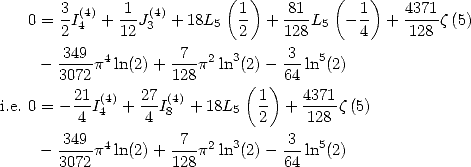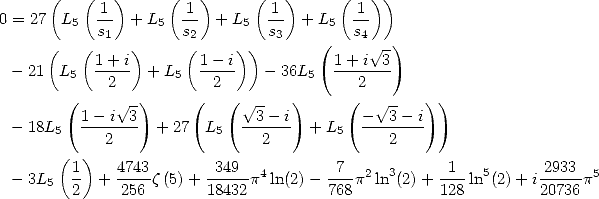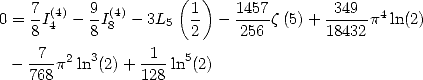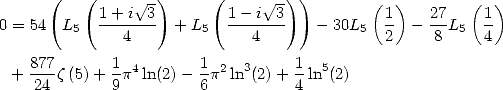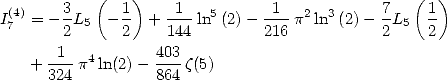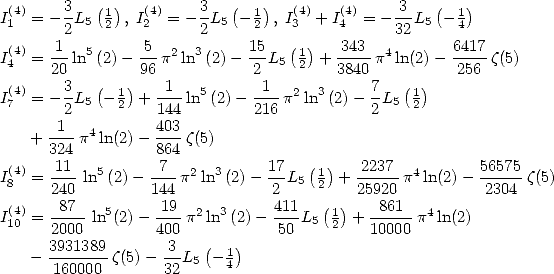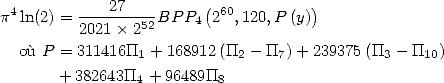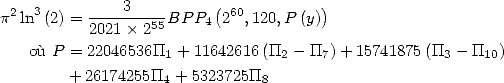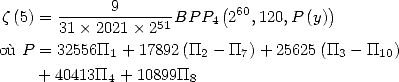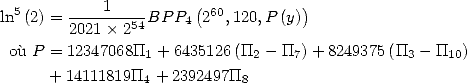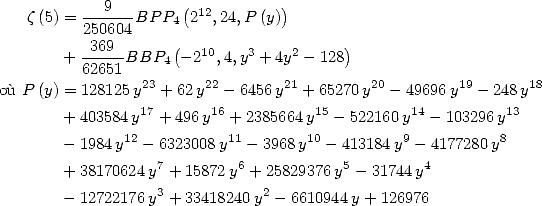|
The world of Pi - V2.57 modif. 13/04/2013 |
|
|
|
6
Formulae BBP in base 2 : 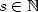 ,
, ,
,  in
in 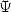
6.1 The considered integrals
In the worry of decomposing our integrals 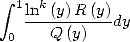 in simpler to calculate integrals, we are interested to
the following "prime" integrals :
in simpler to calculate integrals, we are interested to
the following "prime" integrals :
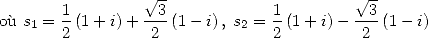 |
(83) |
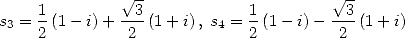 |
(84) |
In [3], Broadhurst establish some relation between the different sums of polylogarithm. However he does not seem to consider the link with integrals. We will try to do so. Which is why we introduce the following integrals :
The link between the 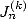 and the is the following :
and the is the following :
6.2 The method
The calculation of the integrals 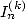 will give linear combination of constants of order
will give linear combination of constants of order 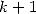 like
like 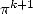 or
or 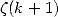 thanks to their expression under
polylogarithm form of order
thanks to their expression under
polylogarithm form of order 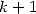 .
But furthermore, we can obtain BBP formula with the
.
But furthermore, we can obtain BBP formula with the 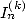 by using what Gery Huvent calls the
denomination tables and which are just the expressions
by using what Gery Huvent calls the
denomination tables and which are just the expressions 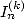 in the form of integrals
in the form of integrals 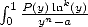 whom we have seen the direct expression under BBP serie form with the
formula (69).
We just need to obtain BBP series for the precise constant that we are
interested in, which boils down to use a certain linear combination of
whom we have seen the direct expression under BBP serie form with the
formula (69).
We just need to obtain BBP series for the precise constant that we are
interested in, which boils down to use a certain linear combination of 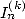 .
For this, we intoduce normally the linear form
.
For this, we intoduce normally the linear form 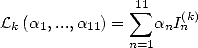 . Then we impose some relation between the
. Then we impose some relation between the 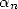 so to cancel out the coefficients in fronts of the unwanted constants.
We then get a BBP serie for the remainder,
so to cancel out the coefficients in fronts of the unwanted constants.
We then get a BBP serie for the remainder, 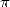 or
or 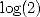 or a lot more other things!
Here is the denominator table. The method is then detailled with an
example.
or a lot more other things!
Here is the denominator table. The method is then detailled with an
example.
where 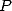 is
a polynomial with integers coefficient which depends both of
is
a polynomial with integers coefficient which depends both of 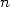 and
of the chosen denominator.
and
of the chosen denominator.
6.3
Formulae for 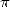 ,
, 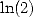 ,
, 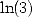 and
and 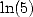
In the case where 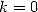 ,
we get, by a calculation of integrals
,
we get, by a calculation of integrals
6.3.1
BBP formulae applications for 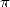
So to get some formula for 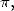 we
impose the following relations :
we
impose the following relations :
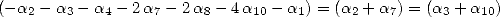
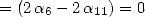 .
.
So we get
So to get some BBP formula with few terms, we
can in a first of all fix 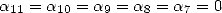 ,
which gives
,
which gives
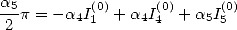 |
(113) |
We then consult the denominator table. To
simplify a sum that calls 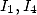 and
and 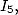 we can write each integral under the form
we can write each integral under the form 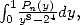
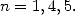 Hence
Hence
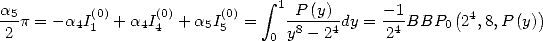 |
(114) |
where 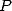 is
a polynomial whose coefficients depends on
is
a polynomial whose coefficients depends on 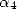 and
and 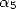 . If we fix
. If we fix 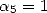 and
and 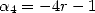 we get the formula by
Adamchik-Wagon (cf [6] )
we get the formula by
Adamchik-Wagon (cf [6] )
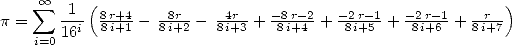 |
(Adamchik-Wagon) |
The choice of 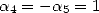 give the formula by Plouffe (61).
We can now look for a denominator in
give the formula by Plouffe (61).
We can now look for a denominator in 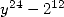 . We take then the formula (111)
and we simply fix
. We take then the formula (111)
and we simply fix 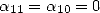 .
.
We choose the other coefficients so to cancel
out the most coefficients of 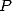 (by
imposing
(by
imposing 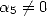 ).
).
The best choice seems to be
![[ai] = (a1,...,a11) = (0,- 1,0,1,1,0,1,-1,-1,0,0)](../mathematiciens/huvent/hyperg367x.gif) which
gives
which
gives
We can also look for a denominator in 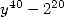 by fixing
by fixing 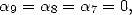 the best choice
seems to be
the best choice
seems to be
![[a ] = (a ,...,a ) = (0,0,0,0,-2,1,0,0,0,0,1)
i 1 11](../mathematiciens/huvent/hyperg371x.gif) which gives
which gives
In fact it turns out that the last formula 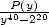 can be simplified to
can be simplified to 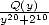 , which gives the alternated formula :
, which gives the alternated formula :
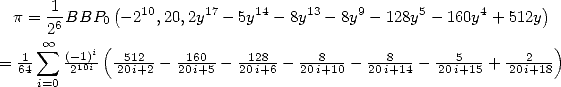 |
(Bellard) (119) |
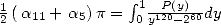 , we just need to choose the right
, we just need to choose the right 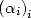 .
The choice that seems to lead to a formula with the least terms
possible is
.
The choice that seems to lead to a formula with the least terms
possible is ![[ai] = (a1,...,a11) = (0,0,0,0,0,1,0,0,- 2,0,1)](../mathematiciens/huvent/hyperg378x.gif) and
gives
and
gives
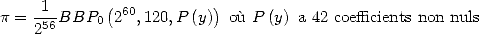 |
(120) |
We can explain 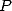 by
writting that
by
writting that
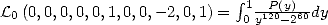 .
.
To finish off, the choice of ![[a] = (0,0,0,0,0,1,0,0,-2,0,1)](../mathematiciens/huvent/hyperg382x.gif) leads to
leads to
And ![[a] = (0,0,0,0,2,0,0,0,-2,0,0)](../mathematiciens/huvent/hyperg384x.gif) gives
gives
6.3.2
BBP formulae for 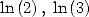 and
and 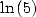
We can apply the same method to obtain some
BBP formula for 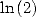 ,
, 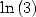 and
and 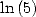 .
.
6.4
Case of polylogarithms of order  : Formulaes of order 2
: Formulaes of order 2
We can notice that for order 1, that is for
the BBP formulae giving 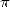 or for example, we had to deal with integrals
with rational fractions. If we now want to get BBP series giving
or for example, we had to deal with integrals
with rational fractions. If we now want to get BBP series giving 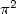 or
or
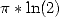 or
or 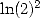 , we need to introduce a logarithm to the
numerator of the integral. More precisely, for a BBP formula of order
, we need to introduce a logarithm to the
numerator of the integral. More precisely, for a BBP formula of order 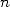 , we
need to consider integrals of type
, we
need to consider integrals of type 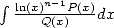 . This is due
to the fact that we then obtain polylogarithm combination of order
. This is due
to the fact that we then obtain polylogarithm combination of order 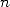 .
.
This is what was done once more by Gery Huvent [12], noting as well that the
first series were found by Plouffe and that Broadhurst [3]
provided a few as well. The interest in order 2 is to be able to find
BBP series for a famous constant which is Catalan's constant defined by
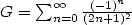 . This
shows, if you are not convinced, that Catalan's constant is
"homogenuous" to an order 2, that is that it is without doubt of the
same nature as
. This
shows, if you are not convinced, that Catalan's constant is
"homogenuous" to an order 2, that is that it is without doubt of the
same nature as 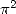 or
or 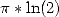 concerning the spread of its digit in base 2 or 16.
concerning the spread of its digit in base 2 or 16.
6.4.1
The classical expression : 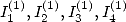 and
and 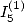
A classical result by Euler is
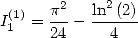 |
(123) |
Which allows us to write that
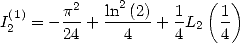 |
(124) |
Kummer's equation for the polylogarithm of order
 is written (cf [4])
is written (cf [4])
The inverse formula is
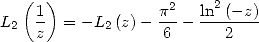 |
(Formule d’inversion) |
and finally the duplication formula in the general case :
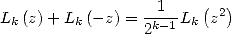 |
(Formule de duplication) |
By applying Kummer's equation for 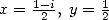 then
then 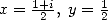 , we get two equality which
added gives
, we get two equality which
added gives
By using the inverse formula for 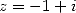 and
and 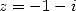 and the duplication formula , we get
and the duplication formula , we get
By duplication, we also have
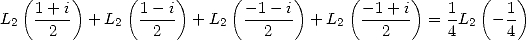 |
(128) |
We therefore deduce
Similarly, Kummer's equation for 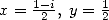 and
and 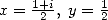 , gives two equality which when
taken away fives a new equality. By then using the inverse formula for
, gives two equality which when
taken away fives a new equality. By then using the inverse formula for 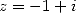 and
and 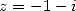 and the duplication formula for
and the duplication formula for 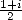 and
and 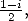 we obtain
we obtain
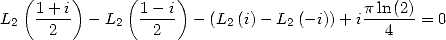 |
(131) |
But 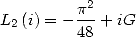 where
where 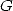 is
Catalan's constant. Hence
is
Catalan's constant. Hence
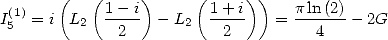 |
(132) |
6.4.2
Calculation of 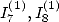 and
and 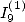
Proposition 2 We have
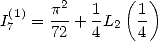 |
(133) |
Proof. Kummer's equation with
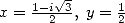 gives the equality
gives the equality
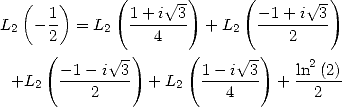
which gives straight
away the wanted result because
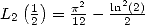 ,
, 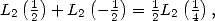
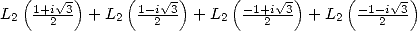
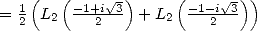 by the duplication formula and
Kummer formula for
by the duplication formula and
Kummer formula for 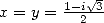 gives
gives 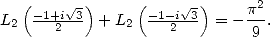 _
_
Proposition 3 We have
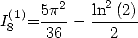 |
(134) |
and
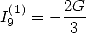 |
(135) |
Proof. Kummer's equation for
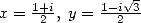 gives, considering
gives, considering
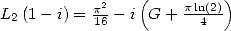

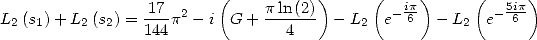 |
(136) |
similarly, Kummer's
equation for
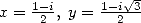 give
give
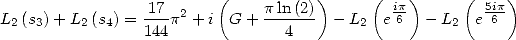 |
(137) |
With the help of the inversion formula
Which allows us to conclude that
and
So we just now need to
calculate the last sum of polylogarithm. But we have gain in simplicity
because those logarithm uses roots of unity.
We therefore use the multiplication formula
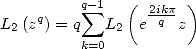 |
(Formule de multiplication) |
which gives with 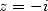 and
and 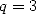
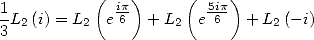 |
(144) |
then with 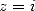 and
and 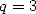
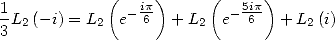 |
(145) |
and allows us to easily conclude. _
6.4.3
Calculating 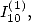 relation between
relation between 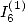 and
and 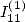
Kummer's equation for 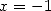 and
and 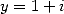 and for
and for 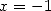 and
and 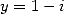 gives two equality which when added gives
gives two equality which when added gives
Which is
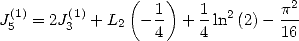 |
(147) |
and allows us to confirm that
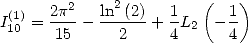 |
(148) |
If, instead of adding them, we substract them, we get
which gives us
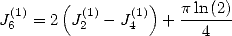 |
(150) |
i.e.
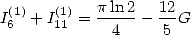 |
(151) |
6.4.4 Application to the determination of BBP formulae
We now consider the linear form 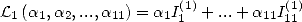 . Taking into account the equalities (123), (124), (129), (130),
(132), (133), (134), (135) and (148), we have
. Taking into account the equalities (123), (124), (129), (130),
(132), (133), (134), (135) and (148), we have
Formulae for 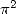 So to obtain BBP formulae for
So to obtain BBP formulae for 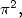 we fix the following equality :
we fix the following equality :
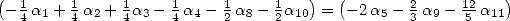
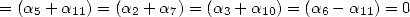 so to obtain the equality
so to obtain the equality
We now just need to use particular variables so to obtain simple formulae.
A few simple alread
known formulae for 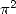
We obtain those formulae by choosing the
integrals who give an denominator of a degree less than in the
correspndance table.
Let us one last time show details an example
:
So to obtain a denominator of the form 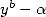 of smaller degree (in that case
of smaller degree (in that case 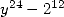 ), we choose
), we choose 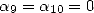 such that we cancel down
such that we cancel down 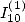 and
and 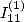 .
OSo we then get
.
OSo we then get
This equality allows to give the general
formula with 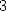 parameters
parameters
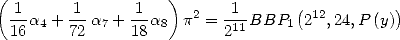 |
(160) |
So not to put too much on this page only the
formulae with parameters that correspond to the denominator in 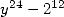 will be given. There exist some who are assoiciated to
other denominators
(for example
will be given. There exist some who are assoiciated to
other denominators
(for example 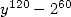 ).
).
Let us look again at the equality (159),
if we choose to fix 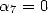 and
and 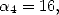 this equality becomes
this equality becomes
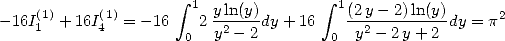 |
(161) |
We can look at this equuality under the form of the sum of BBP formula.
We can bring vack this integral to a
denominator of the form 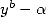 with the help of the corresponding table
so to obtain
with the help of the corresponding table
so to obtain
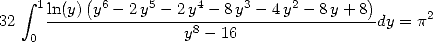 |
(163) |
which gives the following equality
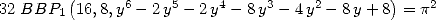 |
(164) |
or
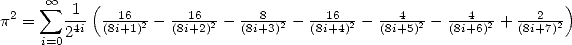 |
(165) |
This equality was already mentioned by Plouffe
in [1]
The choice of 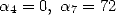 gives
gives
which gives the following formula thanks to Plouffe :
A few simple and new formulae
An other solution consist of keeping the
integrals which gives denominator of the form 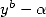 of high degree but adjust the parameters so to gave many
nul coefficients in the BBP formulae.
of high degree but adjust the parameters so to gave many
nul coefficients in the BBP formulae.
A few good choice seems to be the following :
![[ai] = (a1,...,a11) = (1,1,0,0,0,0,- 1,0,0,0,0)](../mathematiciens/huvent/hyperg504x.gif) which
gives the formula to
which
gives the formula to 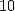 terms
terms
The polynomial 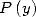 having only odd powers, this formula can be simplified to give
having only odd powers, this formula can be simplified to give
![[ai] = (2,1,0,1,0,0,- 1,- 1,0,0,0)](../mathematiciens/huvent/hyperg509x.gif) which gives
the formula to
which gives
the formula to 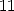 terms
terms
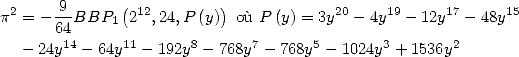
![[a] = (- 2,-1,-1,- 2,0,0,1,0,0,1,0)
i](../mathematiciens/huvent/hyperg512x.gif) which
gives the formula to
which
gives the formula to 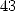 terms (notice the
terms (notice the 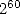 ) :
) :
If we are interested in formula with the least
term, let us state that other formulae with 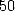 terms
(
terms
(![[ai] = (- 1,- 1,0,0,0,0,1,0,0,0,0)](../mathematiciens/huvent/hyperg518x.gif) ) and with
) and with 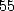 terms (
terms (![[ai] = (- 2,-1,0,-1,0,0,1,1,0,0,0)](../mathematiciens/huvent/hyperg520x.gif) ) exists.
) exists.
We can even look for alternating series, for example
![[ai] = (0,0,0,-2,0,0,0,,0,0,0)](../mathematiciens/huvent/hyperg521x.gif) gives
gives
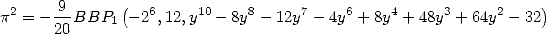 |
(Huvent) |
Notice
The integrals equality allows to write in
different ways  as the sum of BBP formula.
as the sum of BBP formula.
For example, the result by (Huvent)
(![[ai] = (-1,- 1,0,0,0,0,1,0,0,0,0)](../mathematiciens/huvent/hyperg524x.gif) ) gives the
integral equality
) gives the
integral equality
Which can be written
Formulae for the constants 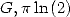 and
and 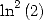 For
For 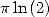
The same method leads to the general formula
for 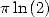 (when we impose a denominator in
(when we impose a denominator in 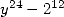 )
)
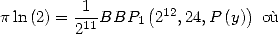 |
(Huvent) |
By adjusting the coefficients 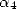 and
and 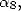 we have formulae with
we have formulae with 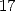 termes of the form
termes of the form
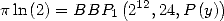
One of the simplest seems to be ![[ai] = (2,- 6,0,4,1,0,6,- 6,-3,0,0)](../mathematiciens/huvent/hyperg538x.gif)
An other formula with 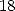 termes is obtained for
termes is obtained for ![[a] = (0,0,0,0,1,0,0,0,-3,0,0)
i](../mathematiciens/huvent/hyperg541x.gif)
To finish ![[ai] = (0,0,0,0,4,1,0,0,0,0,1)](../mathematiciens/huvent/hyperg543x.gif) gives
gives
For Catalan's constant
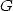
Similarly, by imposing a denominator in 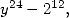 we obtain
we obtain
The most interesting case is obtain when all
the 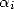 are zero except
are zero except 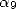 which we let be equal to
which we let be equal to 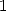 . We
then obtain
. We
then obtain
The interest in this formula resides in the
coefficients of 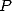 which are all powers of
which are all powers of  .
.
The choice of ![[ai] = (1,- 3,0,2,0,0,3,-3,1,0,0)](../mathematiciens/huvent/hyperg554x.gif) allows to
write
allows to
write
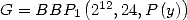 where
where 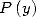 has
has 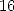 non-zero coefficients.
non-zero coefficients.
To finish ![[a ] = (0,0,0,0,- 1,1,0,0,-1,0,1)
i](../mathematiciens/huvent/hyperg558x.gif) gives
gives 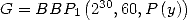 where
where 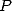 has
has
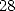 non-nul coefficients.
non-nul coefficients.
Warning 4 It seems that I was the first to have
experimentaly discovery a real formula
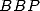 for
for 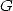 (Mai 2000) without being
able to find proof. The discussion between me and
David Broadhurst with no doubt, but that's not very important...
(Mai 2000) without being
able to find proof. The discussion between me and
David Broadhurst with no doubt, but that's not very important...
For 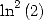
We obtain
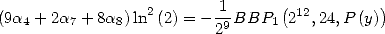 |
(173) |
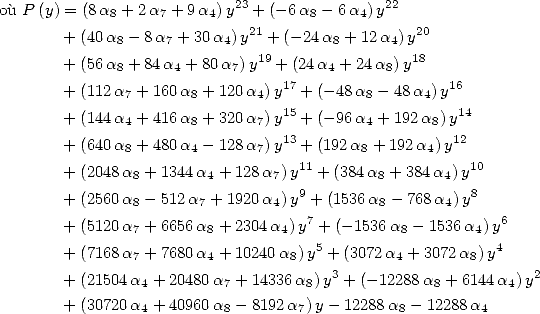
The simplest case is given by ![[ai] = (- 4,- 3,0,0,0,0,3,0,0,0,0)](../mathematiciens/huvent/hyperg567x.gif) which leads
to
which leads
to
The choice of ![[ai] = (- 42,-21,-20,- 40,0,0,21,0,0,20,0)](../mathematiciens/huvent/hyperg569x.gif) leads
to
leads
to 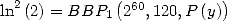 where
where 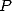 has
has 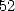 non zero coefficients.
non zero coefficients.
6.4.5 A few composite formulae
In the determination of BBP formulae, we have
systematicly cancel down the coefficients of 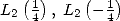 and
and 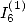 .
If we then decide to keep those term, we can obtain among those
possible formulae, the following result :
.
If we then decide to keep those term, we can obtain among those
possible formulae, the following result :
![[a] = (1,1,0,0,0,0,2,0,0,0,0)](../mathematiciens/huvent/hyperg575x.gif) give
give
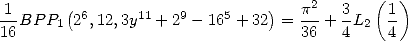 |
(174) |
which can be simplify to
This formula is equivalent to the formula (167).
If we apply this idea to Catalan's constant, we obtain with ![[a] = (0,0,0,0,0,-1,0,0,1,0,0)](../mathematiciens/huvent/hyperg578x.gif) the equality
the equality
Who under serie form gives the two following equality :
The same idea leads, with ![[a] = (0,0,0,0,-4,8,0,0,- 12,0,0)](../mathematiciens/huvent/hyperg581x.gif) to
to
and with ![[a] = (4,8,0,0,- 4,4,12,0,0,0,0)](../mathematiciens/huvent/hyperg583x.gif) to
to
This kind of formula has not been systematically researched.
6.5 Cases of polylogarithms of order 3
The order 3 introduce of course formulae
giving 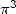 and other
and other 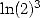 but mostly the famous constant
but mostly the famous constant 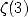 proved irrational by Apéry in 1978 [14] by developping a continued
fraction of a factorial formula which will be mentioned later on.
proved irrational by Apéry in 1978 [14] by developping a continued
fraction of a factorial formula which will be mentioned later on.
This constant stays never the less mysterious, and the BBP formula intuitively shows that this constan is very likely not to be very different from a point of vue of the orderning of it's decimals and hence it's complexity.
Kummer's equation for the triologarithm is
and the inverse formula
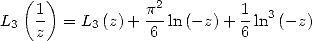 |
(181) |
A classical formula allows to state that
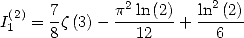 |
(182) |
and by definition
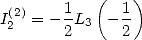 |
(183) |
6.5.1
Calculation of 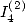
Landen's equation for the trilogarithm is (cf
[4]
)
Applied to 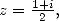 we get (with
we get (with 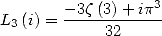 )
)
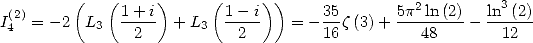 |
(185) |
result implicitely contained in [3].
We deduce by the duplication formula that
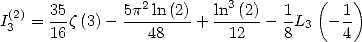 |
(186) |
6.5.2
Calculation of 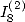
As for the calculation of 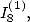 we use Kummer's equation with
we use Kummer's equation with 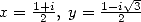 then with
then with
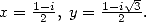 We add
then those two equation we obtain. We simplify those equations with the
help of the valuer of
We add
then those two equation we obtain. We simplify those equations with the
help of the valuer of 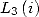 and the equality
and the equality 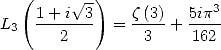 . This allows us to state that
. This allows us to state that
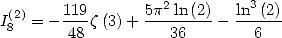 |
(187) |
6.5.3
Relation between 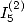 and
and 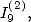 values of
values of 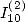
We take the first two equation for the
calculation of 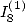 that we substract this time. We then use
the inverse formula with
that we substract this time. We then use
the inverse formula with 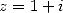 and
and 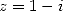 so that we make appear the term
so that we make appear the term 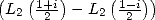 . Finaly one last
application of the inverse formula with
. Finaly one last
application of the inverse formula with 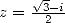 and with
and with 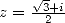 leads to
leads to
Which prove that
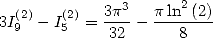 |
(189) |
If we use Kummer's equation with 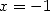 and
and 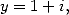 then with
then with 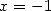 and
and 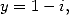 we obtain two equality that we substract. We simplify the
obtained result with the inversion formula applied to
we obtain two equality that we substract. We simplify the
obtained result with the inversion formula applied to 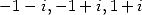 and
and 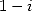 so to obtain
so to obtain
This equality is equivalent with the help of integrals to
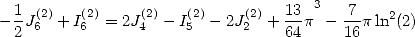 |
(191) |
and gives the relation
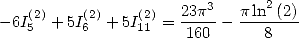 |
(192) |
If, instead of substracting the equality obtained previously, we add
them, we get :
which gives
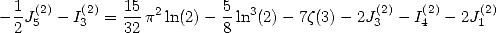 |
(194) |
and furnish
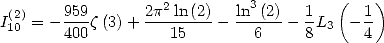 |
(195) |
6.5.4
Calculation fo 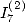
Similarly to the calculation of 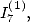 Kummer's equation for the polylogarithm of order
Kummer's equation for the polylogarithm of order 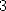 with
with 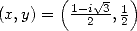 , then the
inverse formula with
, then the
inverse formula with 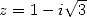 leads immediatly to
leads immediatly to
6.5.5 Application to the determination of BBP formulae
Let us now consider the linear form 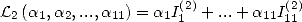 .
Then the previous result allows us to state that
.
Then the previous result allows us to state that
Formulae for 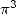 If we look for formulae for
If we look for formulae for 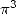 we
cancel down the coefficients of the constants
we
cancel down the coefficients of the constants
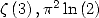 ... to obtain
... to obtain
We can not choose 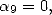 which mean we have to use a denominator in
which mean we have to use a denominator in 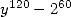 for the BBP formulae giving
for the BBP formulae giving 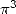 .
In all generality, we hence obtain a BBP formula for
.
In all generality, we hence obtain a BBP formula for 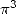 with two parameters (
with two parameters (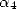 and
and 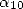 ),
formula that the reader can establish. The simplest formula is hence
obtain for
),
formula that the reader can establish. The simplest formula is hence
obtain for ![[a ] = (0,0,0,0,5,-5,0,0,3,0,- 5)
i](../mathematiciens/huvent/hyperg646x.gif) and with
and with 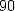 termes. So to wrie it, we introduce the polynomials
termes. So to wrie it, we introduce the polynomials 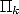 defined by
defined by 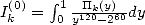 ,
for example
,
for example 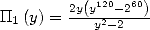 .
.
We then have
This rquality can be written differently.
In fact 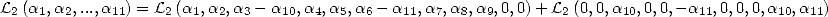
But 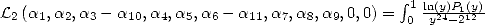 and
and
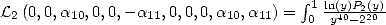 where
where 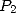 has
has  non-zero coefficients in general, and only
non-zero coefficients in general, and only  if
if 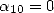 or
or 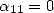 or
or 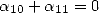 .
.
If we apply this here, we have
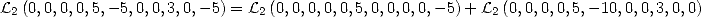 which gives
which gives
This formula can also be written as
Formula for 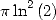 To obtain a simple BBP formula for
To obtain a simple BBP formula for 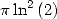 , we apply the same idea as that for
, we apply the same idea as that for 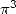 (the problem is the same, we need to use
(the problem is the same, we need to use 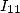 which gives a denominator in
which gives a denominator in 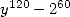 and gives an expression with two parameters)
and gives an expression with two parameters)
We then obtain with ![[ai] = (0,0,0,0,67,-75,0,0,69,0,- 75)](../mathematiciens/huvent/hyperg669x.gif)
This formula can also be written
Compare with those obtain for 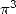 .
.
Formulae for 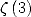 For
For 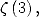 we obtain, if we look for a denominator in
we obtain, if we look for a denominator in 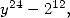
Which give the general formula
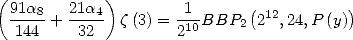 |
(Huvent) |
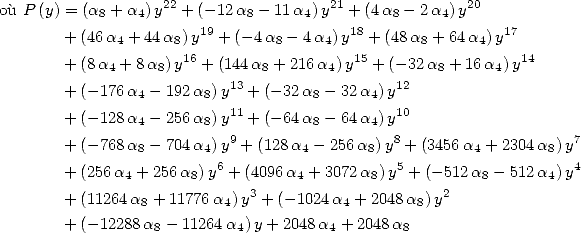
The simplest BBP formula is obtain for
![[a] = (-3,- 1,0,- 2,0,0,1,2,0,0,0)](../mathematiciens/huvent/hyperg679x.gif)
We can also use the following :
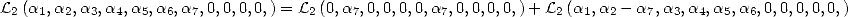
But 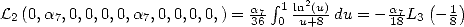 and
and
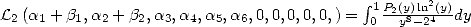
If we then impose 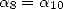 in (203),
we have
in (203),
we have 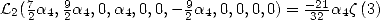
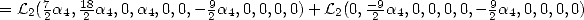 which gives
which gives
Finally the simplest formula for a denominator
in 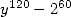 is obtained with
is obtained with
![[ai] = (8,4,5,9,0,0,- 4,1,0,- 5,0)](../mathematiciens/huvent/hyperg689x.gif) and contains
and contains 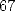 termes.
termes.
Note
5 Similarly here, I thought I was the first to give a
formula for 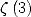 whose proof, a lot less simple but on the
same model, was finished in june 200 with the help of
Raymond Manzoni [5].
whose proof, a lot less simple but on the
same model, was finished in june 200 with the help of
Raymond Manzoni [5].
Formulae for 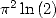 We obtain the following general formula
We obtain the following general formula
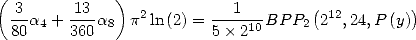 |
(Huvent) |
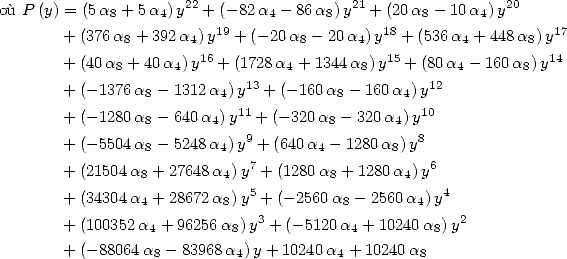
With ![[ai] = (-8,- 3,0,- 5,0,0,3,5,0,0,0)](../mathematiciens/huvent/hyperg695x.gif) , we have the
formula with
, we have the
formula with 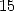 termes
termes
This relation is noteworthy, in fact the
equality (204)
is obtain for ![[ai] = (- 3,-1,0,-2,0,0,1,2,0,0,0)](../mathematiciens/huvent/hyperg698x.gif) .
.
This leads to fix
Then
Finaly the simplest formula with a denominator
in 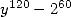 is obtain with
is obtain with
![[ai] = (42,21,25,46,0,0,- 21,4,0,-25,0)](../mathematiciens/huvent/hyperg704x.gif) and has
and has 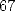 termes.
termes.
Formulae for 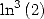 We have the general formula
We have the general formula
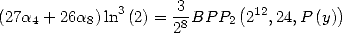 |
(Huvent) |
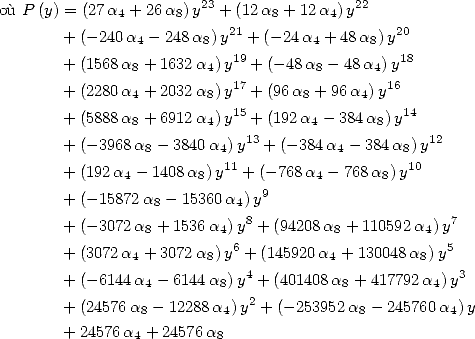
and the simplest formula is ontained for
![[ai] = (- 22,-9,0,-12,0,0,9,12,0,0,0)](../mathematiciens/huvent/hyperg709x.gif)
And the one with a denominator in 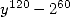 is given by
is given by
![[ai] = (- 202,-99,-100,- 200,0,0,99,0,0,100,0)](../mathematiciens/huvent/hyperg712x.gif)
6.6 Cases of polylogarithm of order 4
6.6.1 The relations
For the polylogarithm of order 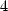 and
and
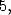 we only have one tool left, this is Kummer's equation.
It is written, with
we only have one tool left, this is Kummer's equation.
It is written, with 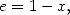
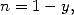
and the inverse formula
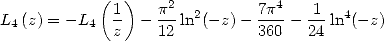 |
(214) |
We then so apply the following method :
- Using Kummer's formula with a particualr couple 
- Eliminating the polylogarith with argument modulus greater than 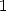 with the inverse formula
with the inverse formula
- Eventual simplification with the help of the duplication formula or
some value of 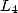 in
in 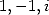 and
and 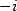 .
.
- With
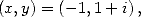 we get
we get
Which with the integrals and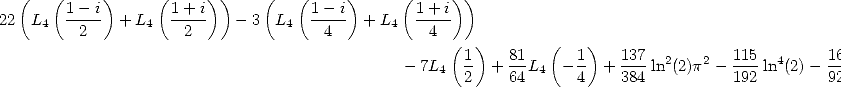
 and
and  becomes
becomes
- With
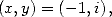 we get
we get
We obtain a second equality with conjugating (or with
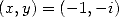 ). We add, or substract the two
equality obtained and by replacing
). We add, or substract the two
equality obtained and by replacing 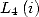 by
by 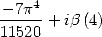 or
or 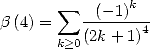 , this gives
, this gives and
- With
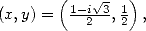 we obtain
we obtain
We then use the multiplication formula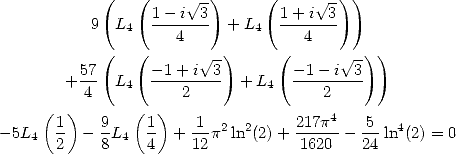
(221)
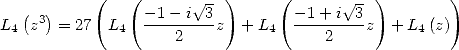
(222) which with
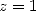 allow us to confirm that
allow us to confirm that 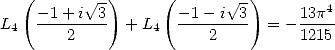
(223) and that
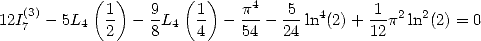
(224) - Finaly, with
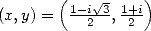 , we
obtain
, we
obtain
By considering the real part and the imaginary part of this expression, we have respectively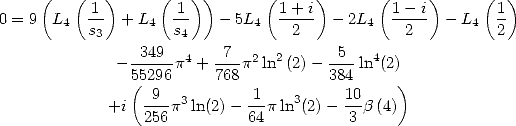
(225)
6.6.2 Application of the determination of the BBP formula
We now consider the linear form 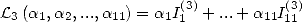 . With the previous formula giving
. With the previous formula giving
6.6.3
Formula for 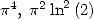 and
and 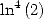
For 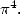 The simplest formula (and the only associated with a denominator in
The simplest formula (and the only associated with a denominator in 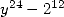 ) is obtained for
) is obtained for ![[ai] = (37,9,0,26,0,0,-9,- 27,0,0,0)](../mathematiciens/huvent/hyperg753x.gif) and gives
and gives
There exist a formula with two parameters with
a denominator in 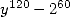 , the simplest is given by
, the simplest is given by ![[ai] = (34,18,25,41,0,0,- 18,18,0,-25,0)](../mathematiciens/huvent/hyperg756x.gif)
For 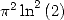 The simplest formula is obtained with
The simplest formula is obtained with
![[ai] = (- 10381,-3303,0,- 6836,0,0,3303,6957,0,0,0)](../mathematiciens/huvent/hyperg758x.gif) and gives
and gives
For 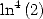 Wiht
Wiht ![[ai] = (-18932,- 6849,0,- 11176,0,0,6849,11322,0,0,0),](../mathematiciens/huvent/hyperg761x.gif) we get
we get
The case of 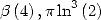 and
and
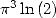 It is not possible to
determine formulae for those constant, we can only find two independant
relation which are :
It is not possible to
determine formulae for those constant, we can only find two independant
relation which are :
This shows that we only need to find a 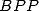 formula for one of those three constant and then we can deduce one for
the two others.
formula for one of those three constant and then we can deduce one for
the two others.
6.7 Case of polylogarithm of order 5
6.7.1 The relations
Broadhurst in [3] shows relations between
the integrals 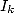 and
and 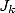 with the help of Kummer's equation
(relations
with the help of Kummer's equation
(relations 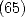 to
to  . Then discover two equality through
numerical mean (relations
. Then discover two equality through
numerical mean (relations 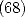 and
and 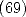 ). He then prove the relation
). He then prove the relation 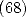 by using the hypergeometric series and Euler's sums. He deduce from it
four equalities for
by using the hypergeometric series and Euler's sums. He deduce from it
four equalities for 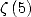 (relation
(relation 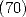 )
)
We can establish those four equalities directly with the help of
Kummer's formula which is written with 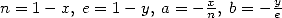
We apply then the same method as that for polylogarithm of order 4.
- With
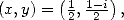 we obtain,
taking into account
we obtain,
taking into account
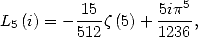
wich gives us
Which can be simplified to, by using
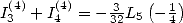
- With
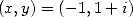 we get
we get
which is equal to
- With
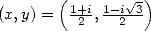 , we
get
, we
get
We simplify this equality with the help of
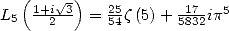 and the multiplication formula
and the multiplication formula 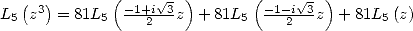 , which with
, which with 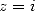 allows us to have
allows us to have 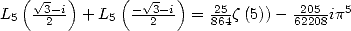 .
.
Hence - With
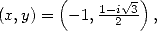 we obtain
we obtain
which gives us
Note
6 The
relation proved by Broadhurst ([3]) correspond to the calculation of 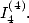 The calculation given here seems
a lot more simple.
The calculation given here seems
a lot more simple.
6.7.2 Application of the determination of the BBP formulae
We now consider the linear form 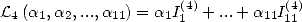 . The previous results gives
. The previous results gives
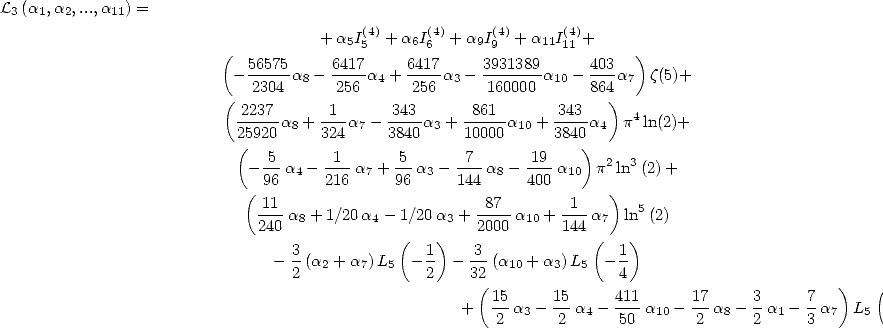 |
(266) |
6.7.3
Formulae for 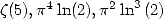 and
and 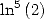
We deduce from this some formulae for the
constants 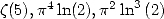 and
and 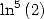 .
We remember that the polynomials are defined by
.
We remember that the polynomials are defined by 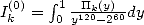 .
.
We hence obtain
with ![[ai] = (311416,168912,239375,382643,0,0,- 168912,96489,0,-239375,0)](../mathematiciens/huvent/hyperg812x.gif)
with ![[ai] = (22046536,11642616,15741875,26174255,0,0,-11642616,5323725,](../mathematiciens/huvent/hyperg814x.gif)
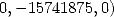
with ![[ai] = (32556,17892,25625,40413,0,0,-17892,10899,0,-25625,0)](../mathematiciens/huvent/hyperg817x.gif)
with ![[ai] = (12347068,6435126,8249375,14111819,0,0,- 6435126,2392497,](../mathematiciens/huvent/hyperg819x.gif)
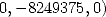
6.7.4 Simplification of those formulae
Those formula can be simplified by making the
term 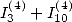 appear. For example
appear. For example 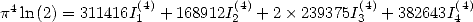
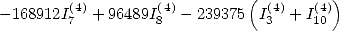 which gives
which gives
Similarly
back to home page