|
The world of Pi - V2.57 modif. 13/04/2013 |
|
|
|
12 Other binomial coefficients
There's not just central binomial
coefficients in life! We can also find some series with other
combination to the denominator, 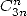 for example. An other idea is also useful :
The numerous series with
for example. An other idea is also useful :
The numerous series with 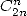 can cleverly be accelerated by taking uniquely part of the terms in
this series, for example by keeping the
can cleverly be accelerated by taking uniquely part of the terms in
this series, for example by keeping the 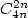 .
Here is a little lot of series giving
.
Here is a little lot of series giving 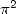 ,
or
,
or 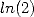 , and who are most likely not all known.
Followed by the proof of a few of them. A few are among the fastest
known rational series!
, and who are most likely not all known.
Followed by the proof of a few of them. A few are among the fastest
known rational series!
Unless otherwise stated, all the series are personal discovery, ignoring any reference I don't know of!
12.1 Primitive formulae
In the whole document, we will call primitive
formula those that minimise the degree of considered polynomials in the
series, and who minimise the number of members of series such as the
BBP binomial considered a few paragraph lates. In fact, for a
polynomial binomial formula 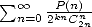 , the decomposition
into even and odd parts (sum on
, the decomposition
into even and odd parts (sum on 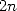 amd
amd 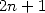 ) gives another serie
) gives another serie 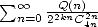 but which is
still equivalent. This said, maybe all the formulae that follows are
not primitive, it's sometime hard to see!
but which is
still equivalent. This said, maybe all the formulae that follows are
not primitive, it's sometime hard to see!
12.2 Factorial polynomials formulae
First of all, we are interested in series of
the form 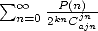 , generalisation
of the previously seen central binomial series
, generalisation
of the previously seen central binomial series 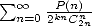 .
.
- With
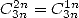 :
:
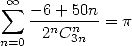 |
(485) |
Such a simplicity, it's beautiful...
We have 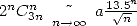 ,
which allows us to conclude that the previous serie gives just a bit
more than one decimal per term, i.e. a speed of roughly
,
which allows us to conclude that the previous serie gives just a bit
more than one decimal per term, i.e. a speed of roughly 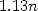 .
.
- With
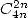 :
:
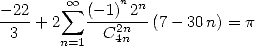 |
(Guillera) |
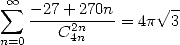 |
(486) |
whom I give two proofs after all those formulae.
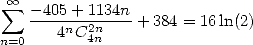 |
(487) |
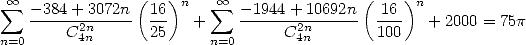
this last fform is not random... as we will see in part 12.4. [link].
Note that 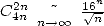 which is
not uninteresting from a calculation point of view! But wait to see the
rest....
which is
not uninteresting from a calculation point of view! But wait to see the
rest....
I remind you here that if I write 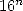 ,
this means that we already gains more than one decimal by iteration.
The exact calculation is done by using the decimal logarithm (because
it's the reciprocal of the function
,
this means that we already gains more than one decimal by iteration.
The exact calculation is done by using the decimal logarithm (because
it's the reciprocal of the function 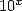 hence this gives us
hence this gives us  the number of decimals, in base 10,
equivalentes to the given number) Here,
the number of decimals, in base 10,
equivalentes to the given number) Here, 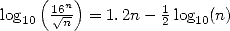 is the
is the 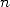 are very big in front of
are very big in front of 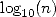 very quickly.
very quickly.
- With
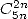
I found nothing.... which does not mean there exist nothing !
- With
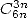 :
:
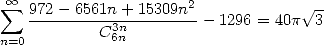 |
(488) |
Note that 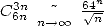
- With
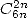 :
:
The last formula is among those that make a 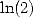 appear but no
appear but no 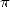 for the same power in the denominator...
for the same power in the denominator...
Note that 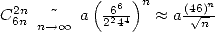 .
.
- With
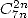 :
:
It's the order of Bellard's
relation. It's a particular order, because  is
an odd number ( !).
Numeriquely, it's the only order
is
an odd number ( !).
Numeriquely, it's the only order 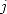 (at least I think so) for which we can find a coefficient
(at least I think so) for which we can find a coefficient 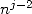 implied.
implied.
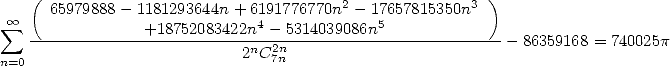 |
(492) |
but also
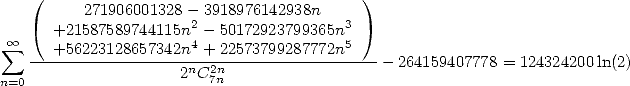 |
(493) |
Concerning the speed of the convergence, we
have 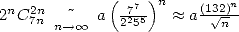
- With
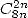 :
:
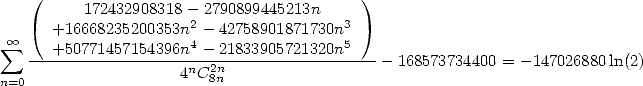 |
(494) |
With 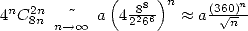
- With
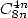 :
:
We have 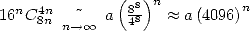
- With
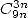 :
:
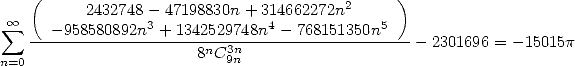 |
(497) |
This time, we have 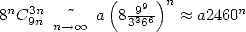
- With
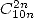 :
:
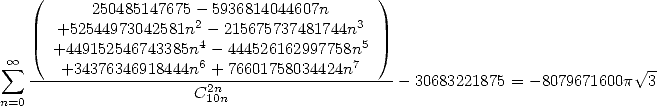 |
(498) |
At equivalent levels, we have 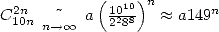
- With
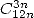 :
:
 |
(499) |
With 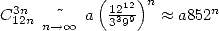
- With
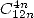 :
:
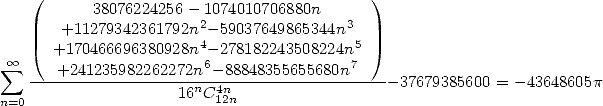 |
(500) |
 |
(501) |
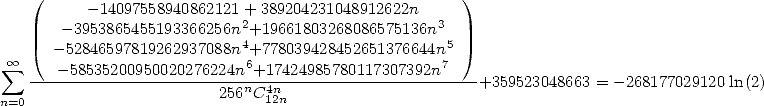 |
(502) |
The speed is 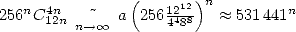
- With
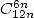 :
:
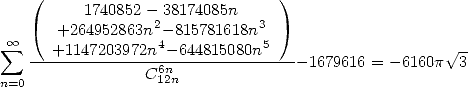 |
(503) |
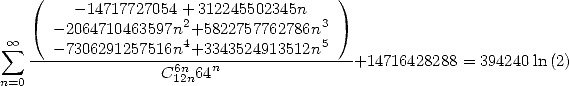 |
(504) |
the speed is 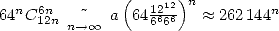 :
:
- With
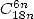 :
:
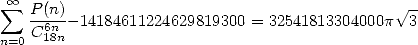 |
(505) |
with 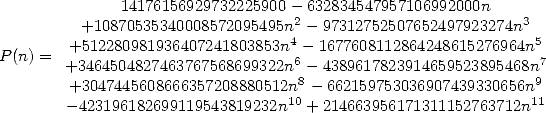
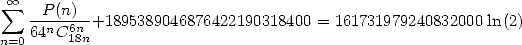 |
(506) |
with 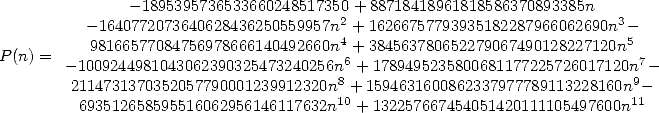
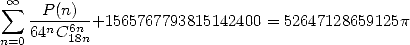 |
(507) |
with 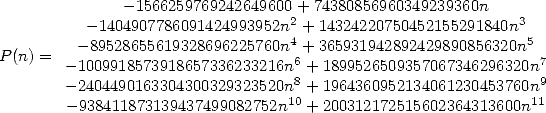
Note on the way that 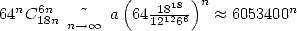 ! ! The last formula adds a bit
more than 6 new decimals at each iteration ! It is now better than the best
rational series of Ramanujan !
! ! The last formula adds a bit
more than 6 new decimals at each iteration ! It is now better than the best
rational series of Ramanujan !
- With
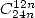 :
:
 |
(508) |
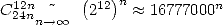 . Impossible unfortunatly to find a formula for
. Impossible unfortunatly to find a formula for 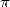 .
.
- With
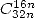 :
:
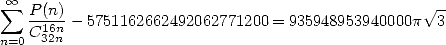 |
(509) |
where 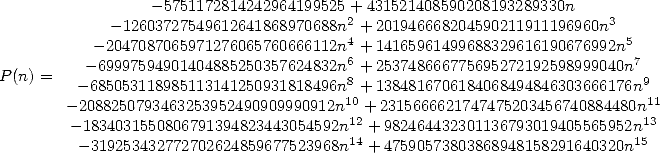
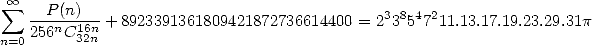 |
(510) |
where 
but also
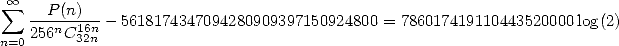
where 
And if we look at the speed of convergence, we get
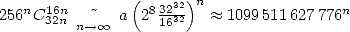 which gives at least 12 new decimals at each step of the
serie !
which gives at least 12 new decimals at each step of the
serie !
Even with it's apparent complexity, it's a rational serie, hence simple to put to work. The calculation of the central binomial coefficeint can as well be done in a recursive way from one step to the next.
- With
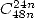 :
:
where 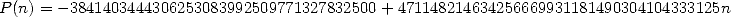
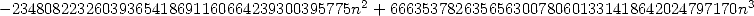
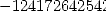

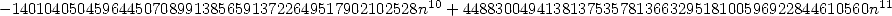
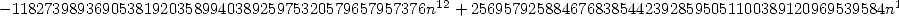
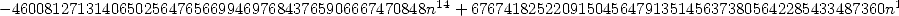
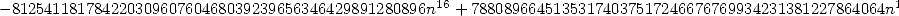
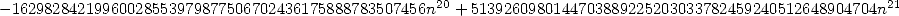
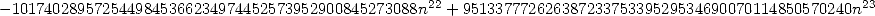
12.3 So, what to make of all of this ?
Several things need to be noted :
- The big coefficients in front of the constants can be generally factorised into product of simple prime numbers, but this does not give much information on the nature of the coefficients.... the one inside the brackets they on the other hand contains big prime factors.
Exemple :
In dront of the coefficient of 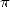 of
the last serie (denominator of the fraction in fron of the serie), we
have
of
the last serie (denominator of the fraction in fron of the serie), we
have 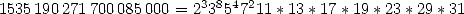 but on the other hand the first coeefient of the
brackets is factorise as follow :
but on the other hand the first coeefient of the
brackets is factorise as follow : 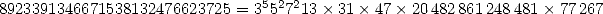 (which is a lot less simple !).
(which is a lot less simple !).
- Second of all, we can already note that at
each order there exists some relation with
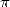 and the logarithm, we can find series wuth null sums like we did for
the BBP series. I think that they are done "mechanically" and that
there must exists a polynomial
and the logarithm, we can find series wuth null sums like we did for
the BBP series. I think that they are done "mechanically" and that
there must exists a polynomial 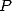 of
degree of at least
of
degree of at least 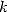 which cancel
which cancel 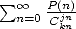 . But I don't
have the proof.
. But I don't
have the proof. - Then, it seems that only well determined
constants can be represented under this form. For my part, with this
kind of exploration, I have never find anything other than
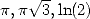 . No
. No 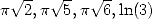 or
or 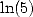 at the horizon... I can understand for
at the horizon... I can understand for 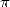 ,
but for the logarithm it's quite surprising!
,
but for the logarithm it's quite surprising! - We can also notice that the repartition of
the signs is so regular (especially in this two by two presentation in
the brackets!) to give a constant, that seems not to have an existance
more justified than an other... unless if
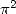 or
or 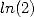 , are very important... Furthermore,
between the formulae for
, are very important... Furthermore,
between the formulae for 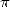 and the formulae for
and the formulae for 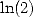 , the coefficients are of same order and
same sign.
, the coefficients are of same order and
same sign. - The coefficients themself are interesting.
They are increasing according to the powers, up to a point, and then
decreasing for the rest, as if they had reach a maximum. This
phenominum is particularly visible with the presentation of the serie
in
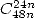 where we can obswerve the maximal coefficient comes in
front of
where we can obswerve the maximal coefficient comes in
front of 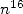 (and by coincindence, a power of
(and by coincindence, a power of  and a third of 48 !).
and a third of 48 !). - We can finnaly notice that apart from the
case
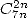 , we have in general some formulae for combination of
kind
, we have in general some formulae for combination of
kind 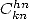 , where
, where 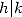 . And thanks to the properties of
combinations, we know that a formula with
. And thanks to the properties of
combinations, we know that a formula with 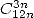 is also a formula with
is also a formula with 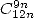 since
since 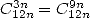 . We can already create a little table of formulae that
have to naturaly appear. In fact, we will notice that between all those
formulae there are a few charecteristics that come back. Hence, there
systematicly exist some formula of kind
. We can already create a little table of formulae that
have to naturaly appear. In fact, we will notice that between all those
formulae there are a few charecteristics that come back. Hence, there
systematicly exist some formula of kind 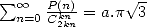 where
where 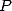 is
of degree
is
of degree 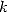 and
and 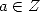 . We also have formulae for
. We also have formulae for 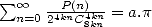 and
and 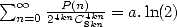 .
This last point is confirm by the article [7]. For the
.
This last point is confirm by the article [7]. For the 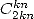 we often have some
we often have some 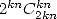 but not always (
but not always (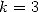 ).
For the
).
For the 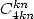 we always have some
we always have some 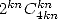 and sometimes some
and sometimes some 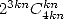 (because
(because 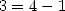 !).For the
!).For the 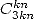 we have some series with
we have some series with 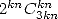 uniquely it seems to me. In all cases, if there is no
powers of
uniquely it seems to me. In all cases, if there is no
powers of  , we found a serie giving
, we found a serie giving 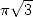 .
If there is a power of 2, we have
.
If there is a power of 2, we have 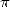 or
or
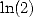 . Easy ! For all
those formulae, with a
. Easy ! For all
those formulae, with a 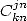 the polynomial
the polynomial 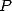 function of
function of 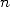 used in the numerator has a degree of at most
used in the numerator has a degree of at most 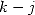 or most of the time
or most of the time 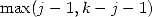 .
.
Note 24 Since I wrote this document, I found an article
printed in octobre 2001 [7] which present
the fundamental research principles of such formulae, and which shows
that we can find some series as fast as we with with the central
binomial coefficients of type 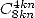 .
.
12.4 Proofs
Those formulae seems difficult to proof because the functions they represent and hence the differential equations that they satisfy have few chances of being simples...
The differential equations are most likelt very complicated, but we be a bit cunning. Notice that we already know the sum
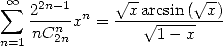 |
(513) |
and that the serie 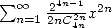 is the even
composant of the previous serie. Then, we have two method that can seem
natural. A third then appeared when following [7].
is the even
composant of the previous serie. Then, we have two method that can seem
natural. A third then appeared when following [7].
- The first consist to build differential equation according to the series using a few of their properties (even part of another serie...). Then, in certain particular cased those differential equations will gives some series:
Let us pay attention to the case of the serie 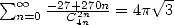 .
.
First of all, we have 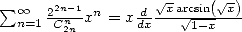 . We need therefore to extract to the first serie 513
part of it's members (those in
. We need therefore to extract to the first serie 513
part of it's members (those in 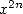 ).
We introduce
).
We introduce
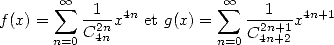 |
(514) |
They are, more or less, the even and odd
composant of 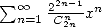 ... more
precisely,
... more
precisely,
Let us now find a relation between the
functions 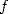 and
and 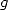 :
:
from which if we derive the relation from 515, we get
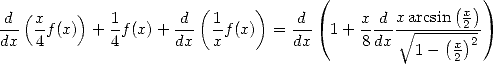 |
(518) |
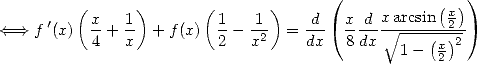 |
(519) |
The right hand side is not very nice, but it
contains a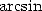 . We just now need to let
. We just now need to let 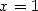 to find
to find
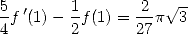 |
(520) |
let
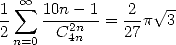 |
(521) |
and it is the serie we were looking for.
We can also let  to find
to find
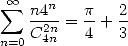 |
(522) |
this also allows to find nearly the same
relations for 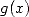 .
.
Finnaly, we can use the famous relation 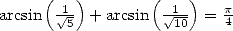 to obtain
to obtain
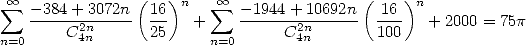 |
(523) |
This case works we find ourself with the two
equations for 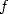 and
and 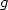 ,
which allows us to come out with a quite useful differential equation.
If we divide in the same way in three part so for example to find some
series in
,
which allows us to come out with a quite useful differential equation.
If we divide in the same way in three part so for example to find some
series in 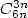 , nothing is garented ! In a general way, the
differential equations will most likely be unsolvable, but we can use
them to find a few relations.
, nothing is garented ! In a general way, the
differential equations will most likely be unsolvable, but we can use
them to find a few relations.
- The other method, which came from Gery Huvent , consist of explicitely calculating
certain series which are pieces of other series, by hoping that
simplifications will be possible. For this. we use the fact that if we
denote
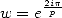 the
the 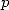 -th
root of unity, we have
-th
root of unity, we have 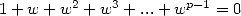 . So with
. So with 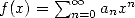
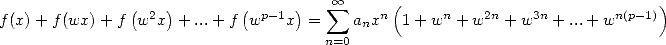
(524)
when 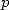 is
prime, two cases are possible:
is
prime, two cases are possible: 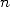 is
not a multiple of
is
not a multiple of 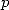 , so since the
, so since the 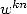 ,
,
![k (- [[0,p- 1]]](../mathematiciens/huvent/hyperg1498x.gif) are the
are the 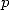 -th
distinct root of unity,
-th
distinct root of unity, 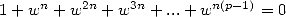 . If
. If 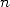 is
a multiple of
is
a multiple of 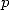 , each
, each 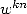 is worth
is worth 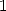 , hence
, hence 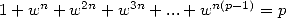 . With all of
this, we obtain the sum only on the multiples of
. With all of
this, we obtain the sum only on the multiples of 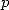 ,
i.e.
,
i.e.
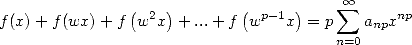 |
(525) |
Let us apply all of this without further ado ! But I will only detail one case, because it is quite a lot of work still...
Let us take the case 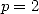 with the serie
with the serie 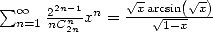 .
.
We obtain on one hand
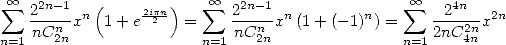 |
(526) |
and on the other
By bringing those two expression together and
composing with 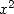 , we obtain
, we obtain
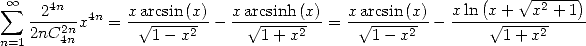 |
(528) |

We can see that we can directly obtain with
this form a serie giving 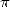 since we can cancel thw term in front of the logarithm (which we then
obtain a diverging series if we had the idea to multiply the expression
by
since we can cancel thw term in front of the logarithm (which we then
obtain a diverging series if we had the idea to multiply the expression
by  and take
and take 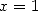 ...). We need to derive the serie 528, which after
multiplication by
...). We need to derive the serie 528, which after
multiplication by  gives:
gives:
it's not very nice... but by doing 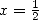 , we get
, we get
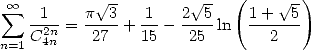 |
(530) |
and we can also use an extra differention so
to make appear a serie in 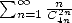 , but that completly
ugly !
, but that completly
ugly !
by letting 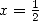 , we get
, we get
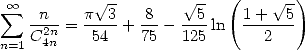 |
(532) |
Starting form here, we can use 530 and 532 to obtain
then
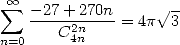 |
(534) |
There we go !
Might as well say that the other series in 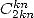 can be deduced in the same way while the method seems
more complicated to use for example for the series in
can be deduced in the same way while the method seems
more complicated to use for example for the series in 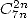 . If we step back to look at the two method explained
above, we note that the first, is based on differential equation, gives
accurate information from wehre comes the coefficients of polynomial
. If we step back to look at the two method explained
above, we note that the first, is based on differential equation, gives
accurate information from wehre comes the coefficients of polynomial 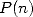 in
in 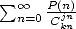 by giving us
directly the formuation formula of those coefficient through
differential equation. The second gives more fredom in concerning the
produced series since we have the exact expression of the serie.
by giving us
directly the formuation formula of those coefficient through
differential equation. The second gives more fredom in concerning the
produced series since we have the exact expression of the serie.
- The method presented now gives the start of
a proof for each formulae above. It comes from the article [7].
This method consist of representing the combination as an integral, then sum it and hence obtain an integral equivalent to the serie, which can be more easily solved. Explenations!
We consider first of all the integral representation of the function Bêta, which gives to integers value the formula
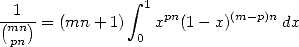
(535) We then sum on
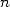 to
obtain the represantation equivalent of the sum under integral form
to
obtain the represantation equivalent of the sum under integral form 
(536) The polynomial
 is
the key to the problem. If it is of degree
is
the key to the problem. If it is of degree  ,
then to obtain the sum of
,
then to obtain the sum of 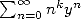 , we derive successively
, we derive successively 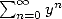 and we multiply each time by
and we multiply each time by 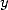 so
to compensate the
so
to compensate the 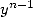 which appears with each derivation,
whichallows us to get
which appears with each derivation,
whichallows us to get 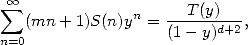
(537) where the polynomial
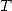 is
of degree
is
of degree 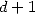 . By writing that
. By writing that
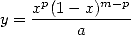
(538) we have finaly
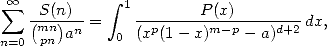
(539) where
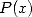 is a polynomial in
is a polynomial in  of degree
of degree 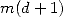 . The roots of the polynomial
. The roots of the polynomial 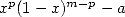 will be fundamental in what concern the apperance of the
constants. In fact, if
will be fundamental in what concern the apperance of the
constants. In fact, if 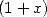 divide this polynomial, we will have
some
divide this polynomial, we will have
some 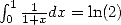 , after
decomposition into simple elements, which appears. If
, after
decomposition into simple elements, which appears. If 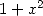 divides
divides 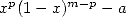 , we will have some
, we will have some 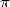 .
The authors did not seems to consider the explicite conditions on the
values
.
The authors did not seems to consider the explicite conditions on the
values 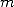 and
and 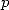 to see any remarkable constants appear, which
we will do, us, for the factorial BBP formulae !
to see any remarkable constants appear, which
we will do, us, for the factorial BBP formulae !
12.5 Fast combinations: Factorial formulae BBP
In the same way as the 12.2, we can
find some factorial formulae having the BBP series form. There are as
fast! We are therefore interested in series with the form 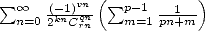 , generalisation of BBP series.
, generalisation of BBP series.
Here's a little anthology, among which the proof for Guillera's formula is given. We will work out during this that the method is not that different from the second one presented for non BBP fast factorial formulae.
Then a method for a more general proof inspired by the idea [7] will have it's own special section !
Note that on the contrary to polynomial
factorial formulae, here it's is very fundamental to find some series
that we will call "primitive" because we can easily see that a formula
in 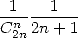 will mechanicly give birth
to a formula in
will mechanicly give birth
to a formula in 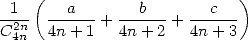 by division of the sum into even parts (
by division of the sum into even parts (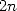 )
and odd parts (
)
and odd parts (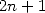 ) then bringing together the terms.
) then bringing together the terms.
To a formula 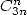 is also associated a formula in
is also associated a formula in 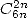 ,
etc... But it is not sure that I have alway written here uniquely some
"primitive" formulae ! Doesn't matter, they are so beautiful :-)
We are at least sure that for a sum
,
etc... But it is not sure that I have alway written here uniquely some
"primitive" formulae ! Doesn't matter, they are so beautiful :-)
We are at least sure that for a sum 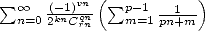 , if
, if 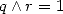 , we have a primitive formula...
, we have a primitive formula...
An example yet again to understand this
deception in the case of binomial BBP formulae: to artificially
accelerate the series we can reorganise the terms in such a way so to
obtain for example 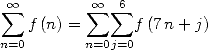 but this can be seen when we factorise the integers
which then have the annoying tendence of being quite simple... Typical
example, has Jesus
Guillera reminded me. The formula
but this can be seen when we factorise the integers
which then have the annoying tendence of being quite simple... Typical
example, has Jesus
Guillera reminded me. The formula
which seems very fast, is essentialy reducable
to the formula 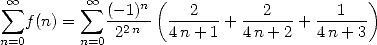 since this breaks down to take
since this breaks down to take 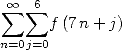 pratically. We can see that the integers coefficients that are used are
very simple (
pratically. We can see that the integers coefficients that are used are
very simple (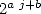 mostly).
mostly).
- With
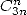 :
:
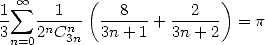 |
(Guillera) |
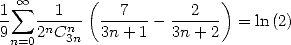 |
(541) |
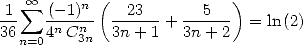 |
(Guillera) |
- With
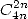 :
:
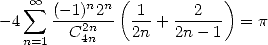 |
(Guillera) |
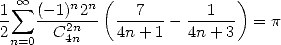 |
(Guillera) |
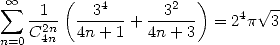 |
(542) |
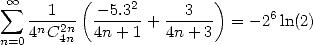 |
(543) |
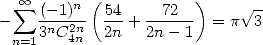 |
(Guillera) |
- With
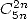 :
:
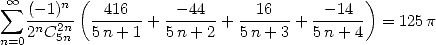 |
(Guillera) |
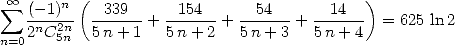 |
(Guillera) |
- With
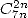 :
:
As with Bellard's formula, we can find a lot
of very interesting sums for the 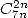
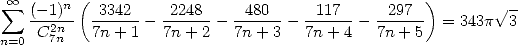 |
(544) |
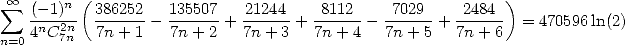 |
(545) |
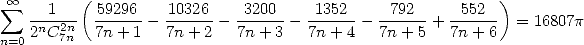 |
(546) |
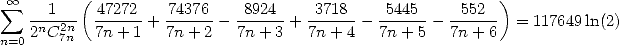 |
(547) |
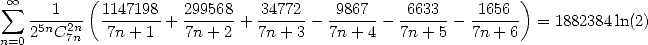 |
(548) |
We also obtain as often some representations
of 0, uniquely for the combination which gives values to some
remarquable constants (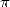 and
and 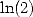 ).
).
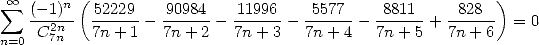 |
(549) |
By looking onto the side of the powers of 3, we can also find some happiness
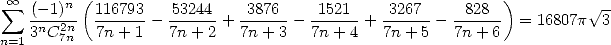 |
(550) |
but to be truthful, that is it!
- With
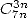
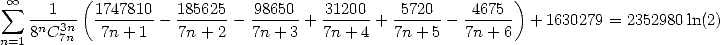 |
(551) |
We don't know any formula for 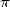 ...
...
- With
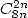 :
:
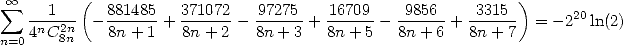 |
(552) |
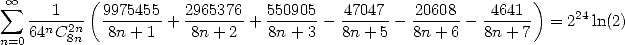 |
(553) |
Note that hear also we can not apparently find
similar formula for 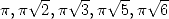 , which is quite
suprising!Furthermore, the
repartition of the signs of the terms in the brackets does not seem to
be random at all... Is it really a primitive formula ? ?
, which is quite
suprising!Furthermore, the
repartition of the signs of the terms in the brackets does not seem to
be random at all... Is it really a primitive formula ? ?
- With
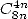 :
:
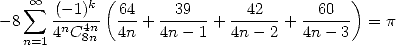 |
(Guillera) |
Jesús Guillera gave this very nice and
simple formula in november 2001 but it is not a real primitive formulae
but is more from a formula in 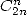 .
.
- With
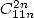 :
:
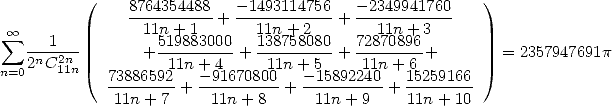 |
(Guillera) |
- With
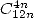 :
:
The following formulae are most likely not primitive formulae but so well.... they are still very nice :-)
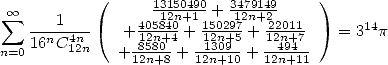 |
(554) |
You will have noticed that 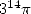 ,
that's really nice !
,
that's really nice !
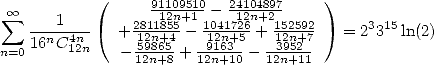 |
(555) |
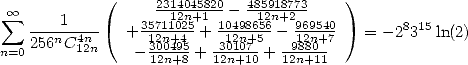 |
(556) |
the speed is of 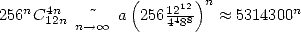
- With
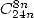 :
:
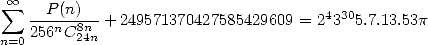 |
(557) |
where 
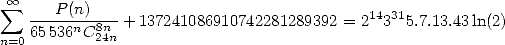 |
(558) |
where 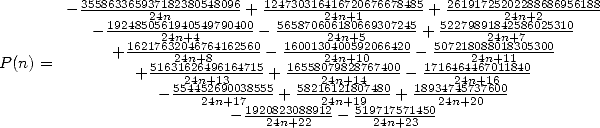
We can also find a function 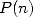 of the same kind as
of the same kind as 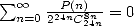 , which
represent the fastest way since a long time to calculate 0 ! !
, which
represent the fastest way since a long time to calculate 0 ! !
- With
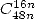 :
:

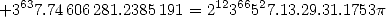
If this is not beautiful.... admire the perfectly regular decrease in the integer coefficients....
Concerning the speed, we have 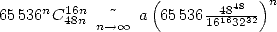 :
: 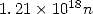 i.e. 18 new decimals at each itteration, great! But
obviously, more terms are needed to be calculated one in the other...
i.e. 18 new decimals at each itteration, great! But
obviously, more terms are needed to be calculated one in the other...
12.6 So, what does it all mmean?
This time again, a few things to note :
- The big coefficients in front of the constant can be factorised into product of fairly simple prime numbers generally, but this does not bring any structal information on the serie...
- The integer coefficients on the
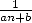 can be factorise but not always with the powers of 2 for
example. This does not give much indication if the serie does or not
follow from an easy cut of a serie with inferior order.
can be factorise but not always with the powers of 2 for
example. This does not give much indication if the serie does or not
follow from an easy cut of a serie with inferior order.
- One inconveniant of those formulae is to
have to use
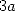 termes in
termes in 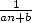 when we are dealing with a coefficient
when we are dealing with a coefficient 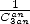 in the serie. For the polynomial series, we had more
in the serie. For the polynomial series, we had more  termes in that case...
termes in that case... - What about greater orders ? That is the constants
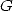 ,
, 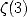 etc... ? the series of kind
[link towards my cubic formula] uses central binomial coefficients, but
with other binomial coefficients? well funily enough we don't really
find any BBP formula in the usual sens, with loads of terms
etc... ? the series of kind
[link towards my cubic formula] uses central binomial coefficients, but
with other binomial coefficients? well funily enough we don't really
find any BBP formula in the usual sens, with loads of terms 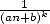 . No explenation to this phenomene if it's not the
complexity of the integral coming into play, which does not give any
remarquable constant, but that's not really satisfying...We need to
study in detail the dividors of the polynomial in the denominators of
the formulae. A few elements later on.
. No explenation to this phenomene if it's not the
complexity of the integral coming into play, which does not give any
remarquable constant, but that's not really satisfying...We need to
study in detail the dividors of the polynomial in the denominators of
the formulae. A few elements later on. - We can ask ourself seing the serie that are
a bit equivalent to polynomials and BBP (and we can even find some for
the values
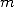 of the coefficinets
of the coefficinets 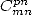 ) if there really exist some "canonic" formulae, some
basic formulae, the simplest possible in the sense of factorial
writting. In fact, we can notice that the BBP series can be put under
polynomial form if we really want it
) if there really exist some "canonic" formulae, some
basic formulae, the simplest possible in the sense of factorial
writting. In fact, we can notice that the BBP series can be put under
polynomial form if we really want it
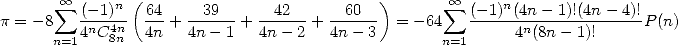
with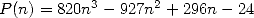 .
But of course, we can see there that we can not put the factorials
under combiatorial form. It is not purely due to notation, the
combination have a real sense and a coherance in the development of
power series as Newton's binomial formula shows.
.
But of course, we can see there that we can not put the factorials
under combiatorial form. It is not purely due to notation, the
combination have a real sense and a coherance in the development of
power series as Newton's binomial formula shows.
In fact, the integral representation shows that often the BBP form is more natural and simple that the polynomial form, but that only an intuitive remark, there is still missing some clarification to the evaluation of the complexity of one of those series compare to the others.
12.7 Typical Proof
Jesús Guillera and myself offer here a
method for proof for those formulae (which does not involve 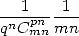 ), this is done to show the
existance of this kind of proof for each formulae, followed by an
application of the first formula of the section. This method was
inspired from the one [7], by atempting to go just
a bit further in the detail...
), this is done to show the
existance of this kind of proof for each formulae, followed by an
application of the first formula of the section. This method was
inspired from the one [7], by atempting to go just
a bit further in the detail...
12.7.1 La méthode
The serie is presented under the form
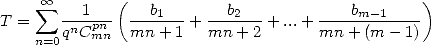 |
(559) |
Great...
We use the integral representration of the function Beta so to directly obtain that
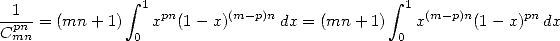 |
(560) |
which gives us the sum
from which we can deal with by decomposition of the denominator into simple elements (careful, I never said it was easy ! :-) ).
Good, but what do we do for the 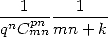 ,
, 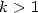 ? ?
? ?
For a fixed 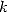 ,
the decomposition into simple elements of
,
the decomposition into simple elements of 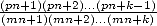 seing it's a rational fraction in n gives a sequence
seing it's a rational fraction in n gives a sequence 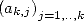 such that
such that
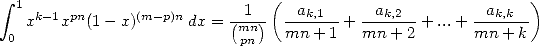 |
(562) |
with 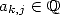 . For all values
. For all values 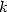 from
from 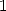 to
to 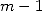 , we then have some sequences
, we then have some sequences 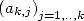 that we can linearly
combine so to form the coefficients
that we can linearly
combine so to form the coefficients 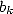 of the sum
of the sum 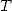 . This is the same as writing down and solving the system
. This is the same as writing down and solving the system
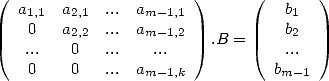 |
(563) |
The vector B contains the coefficients of the
linear combination of the integrals containing 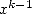 ,
which gives the polynomial
,
which gives the polynomial 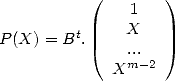 of degree
of degree 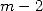 such that
such that
There we go, it's not that hard !
We can also, if we worry about the
construction of formulae and not of proofs, choose a polynomial 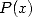 which voluntary simplify certain divisors of the denominator of the
equivalent integral. We then found ourself in a situation which I spend
time on in 12.7.4.
which voluntary simplify certain divisors of the denominator of the
equivalent integral. We then found ourself in a situation which I spend
time on in 12.7.4.
12.7.2 Application : Proof of the first formula
We take yet again the first formula by Guillera
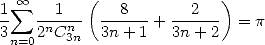 |
(565) |
We use the integral formula

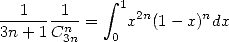 |
(566) |
which is proved by recurrance for example for the pure mathematician! We deduce that
For 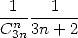 , it's a bit more
complicated, butwe can found our way around anyway by following the
method of the above section, know that
, it's a bit more
complicated, butwe can found our way around anyway by following the
method of the above section, know that
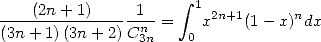 |
(568) |
We have
hence
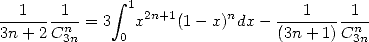 |
(571) |
which is equivalent to considering the famous
polynomial we are looking for is 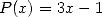 because we have
because we have
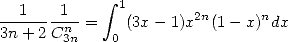 |
(572) |
since the polynomial is simple, we can explicitely determine it, but this will not always be the case (see proof below).
The calculation is now direct
hence finaly by recopying the method of 6.2by Gery Huvent , we have
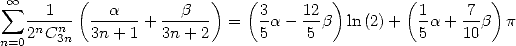 |
(574) |
 We
now choose
We
now choose 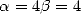 so to cancel down the participation
of our dear
so to cancel down the participation
of our dear 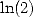 and obtain Guillera.
We can also let
and obtain Guillera.
We can also let 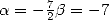 so to obtain 541.
so to obtain 541.
12.7.3
Proof of the formula in 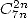
Jesus Guillera and myself now offer you a quick proof of one of the best formula in the packet, 546.
We remind ourself that the principal is to
find a polynomial 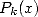 such that
such that
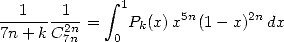
While the solution, for each k, is not unique,
we know that the degree of 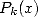 is
is 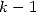 . By the method of linear system, we get
. By the method of linear system, we get

Now, we put it together....
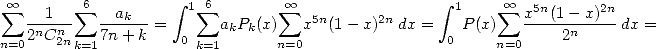
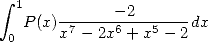
With the 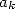 of the formula 546,
we have
of the formula 546,
we have 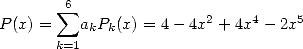
and
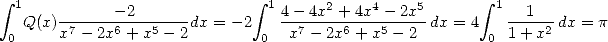 |
(575) |
Incredible, no ? ? That this quite big sum is in fact equivalent to a very simple integral, it's great!
12.7.4 Predictions of formulae
Looking at the proof, we might ask ourself if there exist a way to predict for which combinations there exists a formula. I have not for the moment a complete answer, but a sufficient condition is already quite simple to show.
We have seen in fact with the formula in 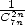 that the integral was equivalent to
that the integral was equivalent to 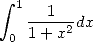 . This comes
from the fact that
. This comes
from the fact that 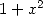 divides
divides 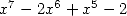 and the polynomial in the
numerator (hence the coefficients) is only used to simplify the other
factors. But for non alternating formulae, the polynomial in the
denominator comes from
and the polynomial in the
numerator (hence the coefficients) is only used to simplify the other
factors. But for non alternating formulae, the polynomial in the
denominator comes from 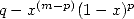 which we will call a
generating polynomial. Starting from that, a sufficient existance
condition for a formula for
which we will call a
generating polynomial. Starting from that, a sufficient existance
condition for a formula for 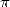 is
that
is
that
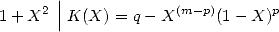
Hence we need that 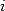 and
and 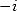 are roots of
are roots of 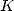 .
In particular, we have for
.
In particular, we have for 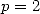 ,
,
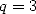 ,
, 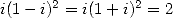 . This
proof the existance for a formula in
. This
proof the existance for a formula in 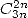 for
for 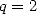 . But since
. But since 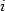 and
and 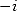 are 4th root of
are 4th root of 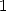 ,
we can multiply
,
we can multiply 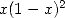 by
by 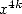 without changing the existance of the roots
without changing the existance of the roots 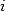 and
and 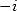 . This then proof the existance of a formula in
. This then proof the existance of a formula in 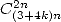 .
.
Let us try to specify the sufficient condition :
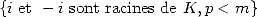
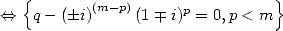
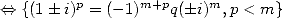
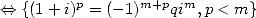 by
conjugate
by
conjugate
![{ }
<==> ( V~ 2)p = q et pp =_ (m + p)p+ m p [2p],p < m
4 2](../mathematiciens/huvent/hyperg1714x.gif) by using modulus and argument
by using modulus and argument
![{ p } { k }
<==> 22 = q, p < m et - p =_ 2m [8] <==> p = 2k, 2 = q, p < m et 7p =_ 2m[8]](../mathematiciens/huvent/hyperg1715x.gif)
Things are clear. So that we can obtain a non
alternating factorial BBP formula thanks to the integral 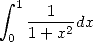 , it is
necessary and sufficient that
, it is
necessary and sufficient that 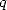 is
a power of
is
a power of  ,
, 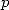 even and smaller than
even and smaller than 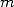 and most of all the great relation of congruence
and most of all the great relation of congruence ![7p =_ 2m [8]](../mathematiciens/huvent/hyperg1721x.gif) . We can easily check that the conditions
. We can easily check that the conditions 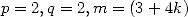 satisfy those
conditions. We also find that the condition is satisfied for
satisfy those
conditions. We also find that the condition is satisfied for 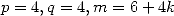 , formulae that I missed in
my experimentations! Just to show, that sometimes the theory is faster
than the pratical... :-)
, formulae that I missed in
my experimentations! Just to show, that sometimes the theory is faster
than the pratical... :-)
By applying the same method to alternating
series, to the roots 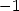 (which allows us to find
(which allows us to find 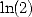 thanks to
thanks to 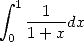 ), to the
polynomial
), to the
polynomial  (so to find
(so to find 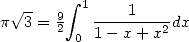 ), we find the following conditions, and hence the
following formulae :
), we find the following conditions, and hence the
following formulae :
For non-alternating series 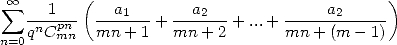
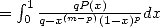
|
|
|
|
|
|
| Pole | Constant | Condition with roots | Condition of existance of pole | Type of existing formula |
|
|
|
|
|
|
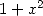 |
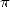 |
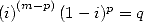 |
![p = 2k, 2k = q,7p =_ 2m [8]](../mathematiciens/huvent/hyperg1735x.gif) |
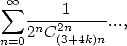 |
|
|
|
|
|
|
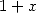 |
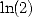 |
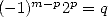 |
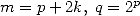 |
Quite a few seing the relation ! |
|
|
|
|
|
|
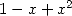 |
 |
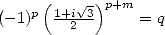
|
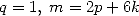 |
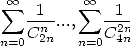 |
|
|
|
|
|
|
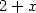 |
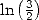 |
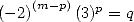 |
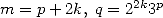 |
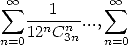 |
|
|
|
|
|
|
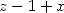 |
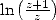 |
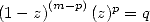 |
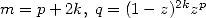 |
... |
|
|
|
|
|
|
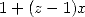 |
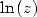 |
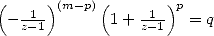 |
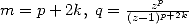 |
... |
|
|
|
|
|
|
| |
Note that when we need a polynomial with complex roots that divides our
generating plynomial, we only need one of the complex root that is root
of this polynomial, by conjugates (due to the fact that the generating
polynomial is real). This table indicates for example why we find so
often some formulae for 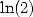 but not always for
but not always for 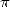 . While we are dealing here with a sufficient
condition and not a necessary one, the conditions on the logarithm
shows that it is probable that we can not obtain any other intigers
logarithm than
. While we are dealing here with a sufficient
condition and not a necessary one, the conditions on the logarithm
shows that it is probable that we can not obtain any other intigers
logarithm than 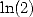 with some integer powers
with some integer powers 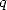 .
.
For alternating series 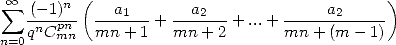
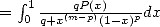
|
|
|
|
|
|
| Pole | Constant | Condition with roots | Condition of existance of pole 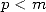 |
Type of existing formula |
|
|
|
|
|
|
 |
 |
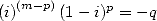 |
![k
p = 2k, 2 = q,7p =_ 2m + 4[8]](../mathematiciens/huvent/hyperg1769x.gif) |
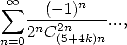 |
|
|
|
|
|
|
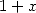 |
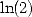 |
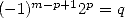 |
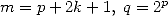 |
Quite a few seing the relation ! |
|
|
|
|
|
|
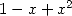 |
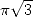 |
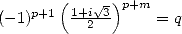 |
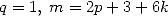 |
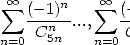 |
|
|
|
|
|
|
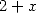 |
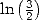 |
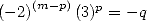 |
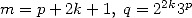 |
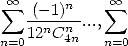 |
|
|
|
|
|
|
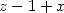 |
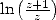 |
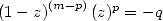 |
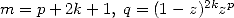 |
... |
|
|
|
|
|
|
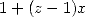 |
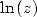 |
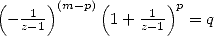 |
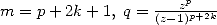 |
... |
|
|
|
|
|
|
| |
12.8 Product of combinaisons
A very interesting questiong concern the
possible presence of several combinations in a serie giving 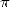 . I
have to admit that I thought this was very improbable, until I
discovered the following formula in december 2001, thanks to
Jesús
Guillera
. I
have to admit that I thought this was very improbable, until I
discovered the following formula in december 2001, thanks to
Jesús
Guillera
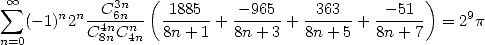 |
(Guillera) |
The same with factorials
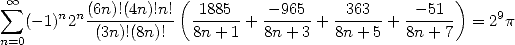 |
(Guillera) |
We also have
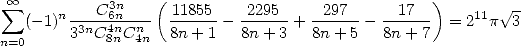 |
(Gourevitch) |
or
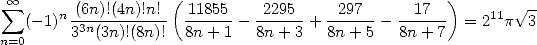 |
(Gourevitch) |
So, where does this comes from ? Well instead of starting from integers power in the integral, we use rational powers and in particular square roots. In fact, considering the integral
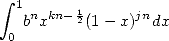 |
(576) |
we obtain sums of the form
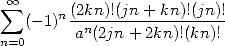 |
(577) |
or for example for 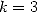 and
and 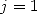
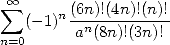 |
(578) |
or even for 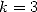 and
and 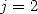
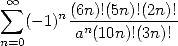 |
(579) |
The BBP sums are then deduced after integration so to give formulae of the type
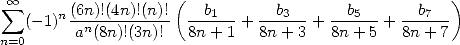 |
(580) |
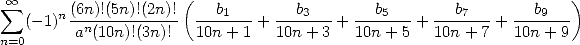 |
(581) |
For the first formula of Guillera, we consider for example the following proof
Proof. 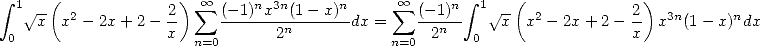
and we then use the known values of 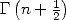 . _
. _
An other example contains
where 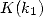 is the elliptical function of first sort in the first singular value,
famous constant of elliptical theory !
is the elliptical function of first sort in the first singular value,
famous constant of elliptical theory !
It is obtained from
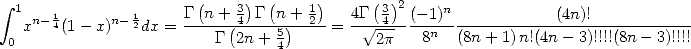 |
(583) |
and
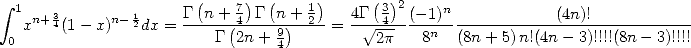 |
(584) |
and the integral
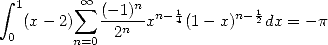 |
(585) |
All of this open some very interesting perspectives !
Equaly note that the BBP form is is a very general form of series in the sense where even the formulae like the ones by Ramanujan can be put under BBP form, like
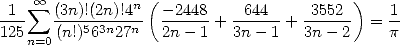 |
(586) |
On the other hand, unfortunatly, we still have not find a method to pove those formulae with the method Bêta...
A lot more details and a few other formulae will be given in the article [13], available sometime soon I hope !
back to home page