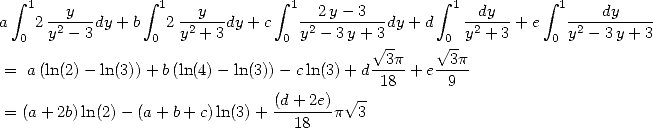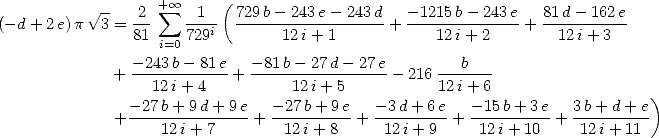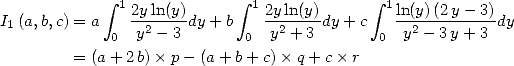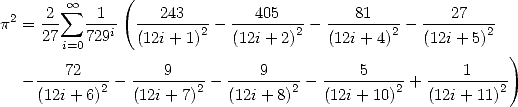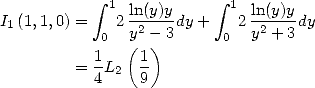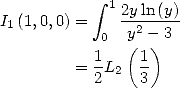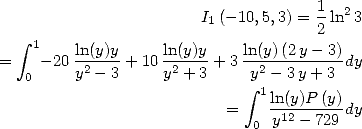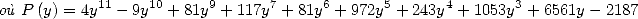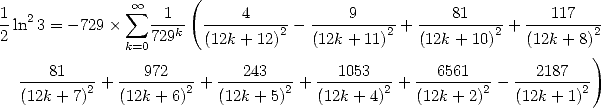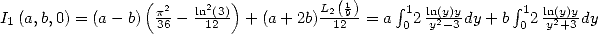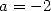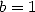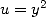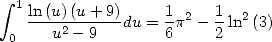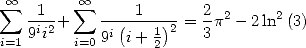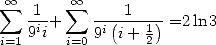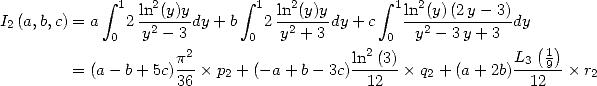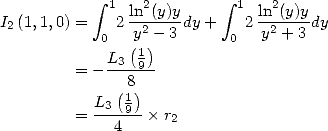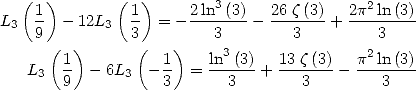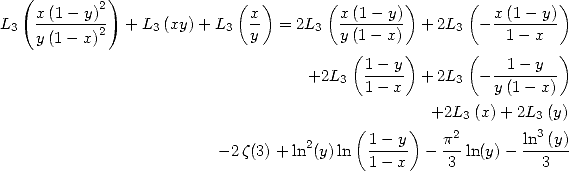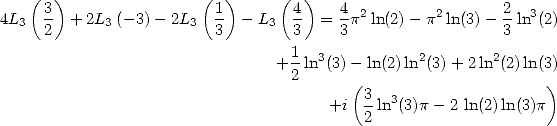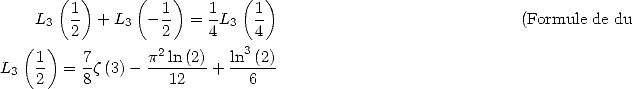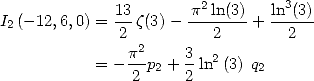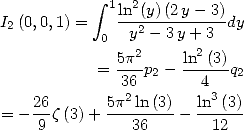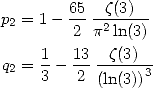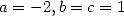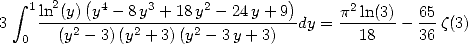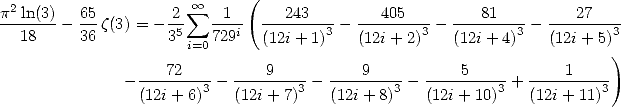|
The world of Pi - V2.57 modif. 13/04/2013 |
|
|
|
7  fixed integers,
fixed integers,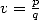 ,
, 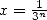 : BBP in base 3
: BBP in base 3
So many results already ! But it's not over yet... in fact,
even if we can not BBP formula for all bases, an important class of BBP
formula was obtained in base 3, which correspond to taking 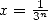 .
Here again, Gery Huvent explained the best
the relations in [12].
.
Here again, Gery Huvent explained the best
the relations in [12].
7.1
Formulae for 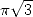
We take the same kind of integrals than that of base 2, but this time it's the 3 that will be omnipresent in the polynomials.
An elementary calculation shows that
By cancelling the coefficients of 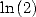 and
and 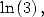 we obtain a formula for
we obtain a formula for 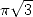 :
:
The following particular case is the most
elegant 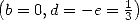 :
:
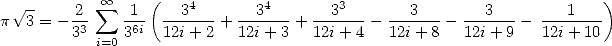 |
(Huvent) |
7.2
Formulae of order : integrales with 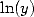
There exist reals 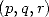 such that
such that
( the two members are linear form in 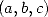 decompose on two different base of the dual of
decompose on two different base of the dual of 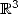 )
)
Plouffe showed that
which under integral form, give
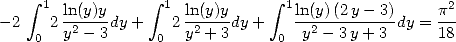 |
(271) |
and correspond to the equality 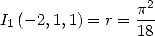 . We can
deduce the value of
. We can
deduce the value of  .
.
But we have
where 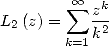
We deduce from it
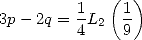 |
(273) |
But Ramanujan proved that
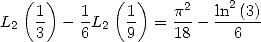 |
(274) |
By using
We deduce from it
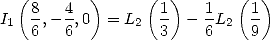 |
(276) |
and
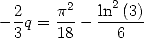 |
(277) |
From (273)
and (277) we get the
values of 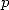 and
and 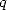 and the equality
and the equality
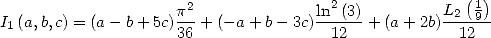 |
(278) |
Note 7 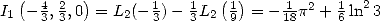 is another relation proved by Ramanujan
.
is another relation proved by Ramanujan
.
7.3
Formulae of order 3 : Integrales
with ln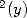
Here again, the order 3 introduce some
formulae giving 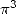 and other
and other 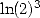 but also
but also 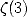 .
.
There exist reals 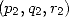 such that
such that
The calculation of 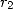 is elementary because
is elementary because
Proposition 11 We have
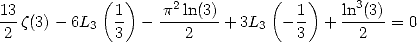 |
(285) |
This relation is equivalent to
Proof. Kummer's equation for the polylogarithm of order 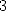 is written
is written
With 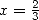 and
and 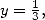 we obtain
we obtain
Landen's equation is
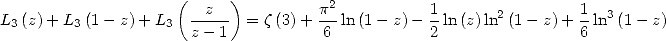 |
(290) |
Applied to 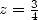 and to
and to
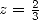 , it allows to
express
, it allows to
express 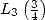 and
and 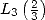 in functions of
in functions of 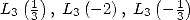 and
and 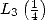 . The
relation
. The
relation
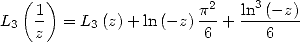 |
(291) |
applied to 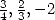 and
and 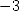 allows to simplify the left member of (289).
allows to simplify the left member of (289).
Then all there is left to do is use the two
following equalities
to conclude. _
With 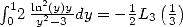 and
and 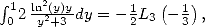 (285)
can be written
(285)
can be written
If we replace 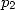 by
it's value compared to
by
it's value compared to 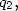 the right hand side of
the right hand side of 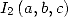 becomes a polynomial of degree
becomes a polynomial of degree 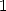 in
in 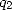 whose coefficient of
whose coefficient of 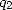 is
equal to
is
equal to 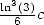 . Hence
. Hence 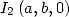 does not depend on
does not depend on 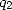 .
After calculation, we get
.
After calculation, we get
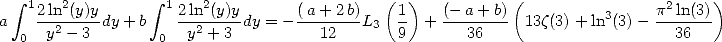 |
(294) |
In particular, we have with 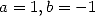
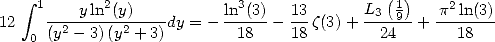 |
(295) |
which gives the equality
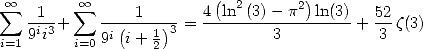 |
(Huvent) |
Note 12 We can also
take 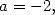
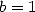 and to a change of variables
and to a change of variables 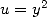 which leads to
which leads to
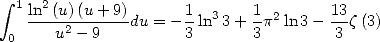 |
(296) |
and to the same equality as for the series.
We just need to calculate the exact value of 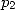 and
and 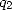 .
.
Proposition 13 We have the equality
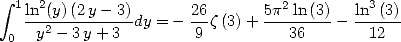 |
(297) |
Proof. Landen's equation applied to 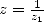 where
where
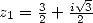 is a root of
is a root of 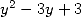 (the other root is
(the other root is 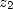 such that
such that
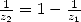 )
give
)
give
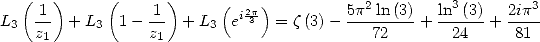 |
(298) |
But 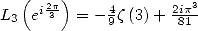 and
and 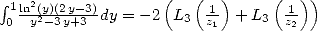 . We
deduce that
. We
deduce that
By using the equations (293)
and (299), we deduce
from it that
And hence
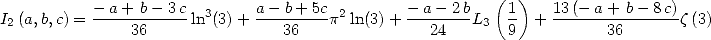 |
(302) |
back to home page