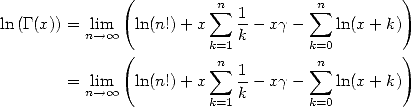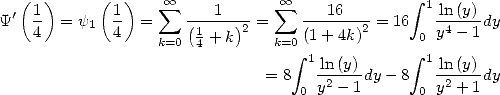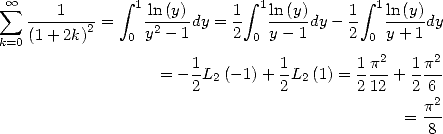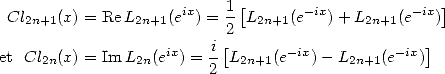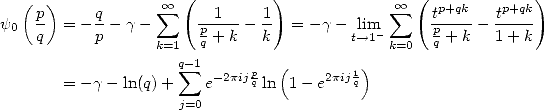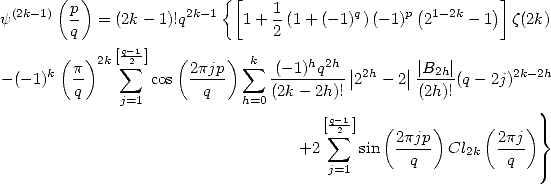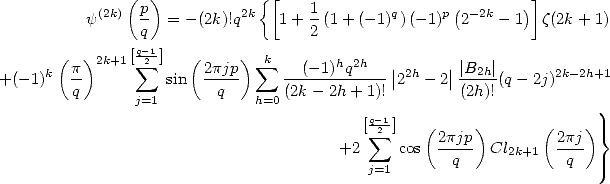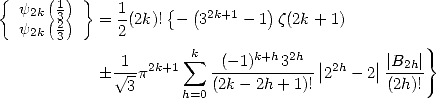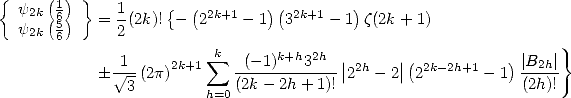9 Polygamma and Clausen

(case fixed integers, , )

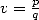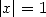An other look at the particular case of the function 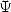... We are starting to corner the problem !

9.1 Polygamma Functions

The polygamma functions are defined for 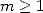by the following relation :

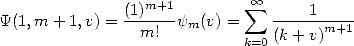(307)

So we are dealling with hypergeometric series :

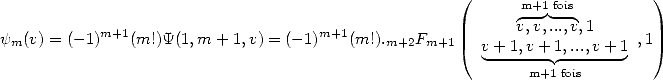(308)

We'll notice that for 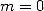, the serie is not convergent, which is why we can use this definition.

However, if I've introduce the polygamma after their series is to make the link with what interest us here, we need to know that the usual definition of the polygamma are done using the famous Gamma function 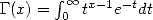. Hence the 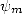functions are in fact the 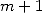-th differention of the logarithm of the Gamma function :

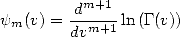(309)

and we can define 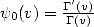which we also call the Digamma function. Why are we doing that by the way?

In fact, I started from the nice formula recalling the function but it seems useful to quickly show why this is all linked to the function . Because, this famous hypergeometric serie gives most of the time only , even if it is hidden !

Let us start from the well know equality 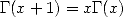to confirm and remind us that the definition of Pochammer's symbol gives us for all in

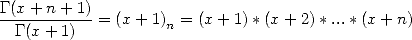(310)

giving the following formula

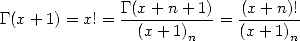(311)

Thanks to the never the less famous equivalence by Stirling extend to the non-integer factorial we have for 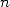near infinity

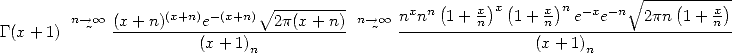(312)

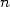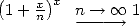by decomposing and sorting the . Then, we notice that and that 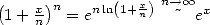and finaly that of course 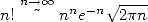thanks to Stirling. This leads us to

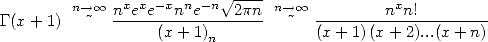(313)

or

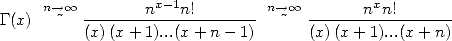(314)

This gives us the logarithmic form of the Gamma function

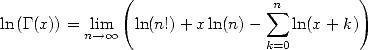(315)

which is equivalent to the formulation of the function by the infinite product of Weierstrass for friends. In fact, by taking into account that 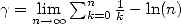, we can write

From there, we can go in crazy direction (which will keep quiet the rigourous justification because we don't want to overload the page) and easily find the polygamma and digamma functions commonly defined. In fact the first diffirentiation gives

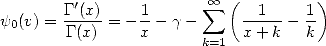(317)

then a second differentiation gives

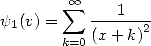(318)

and so on.

Basicly, you've understood it, here we are playing with the Gamma function and it's derivatives.

9.2 The digamma function

We have seen the definition of the digamma function above (317). It is only interesting in the fact that it involves some 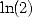and some 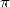, it does not manage to associate the Euler's gamma constant. Hence, we get

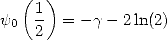(319)

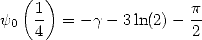(320)

From the formula 317, the constant 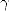is simplified... We need to establish if this constant is homogeneous or not to 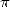or 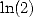 ? it's likely... According to the polygamma and the BBP formulae, we can say that if 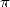of order 1 and 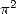 is of oder 2, then 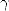is of order ”” or below 1 in all cases...

At the rational points, the digamma function reveals it's intimacy thanks to the theorem on Gauss' digamma, which say that

(321)

for , .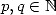

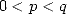We clearly see here the intervention of 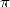, always present in important places !

9.3 Polygamma of order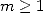

Plouffe but in evidence on his page numerous relation between the polygamma function of order 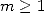and the constants of order 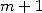for rational parameters.

9.3.1 Link with the integrals of BBP formulae

Even if those relation were only put to light later on, they are nothing less than BBP formula with no powers 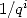. In fact, this comes down to taking a particular integral, and more precisely 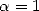in the formula 64.

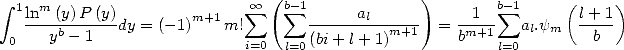(322)

For this reason, the proof of those formulae are done exactly done the same as in the paragraph dedicated to BBP formulae.

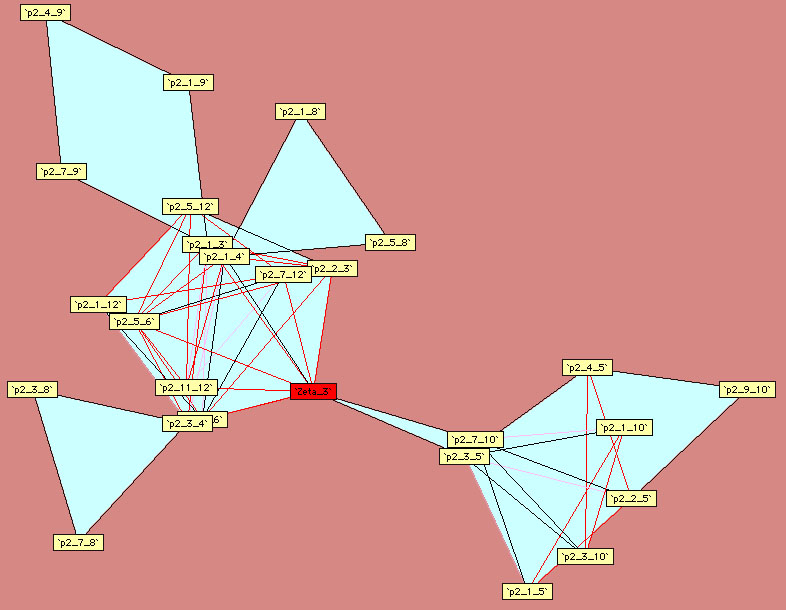
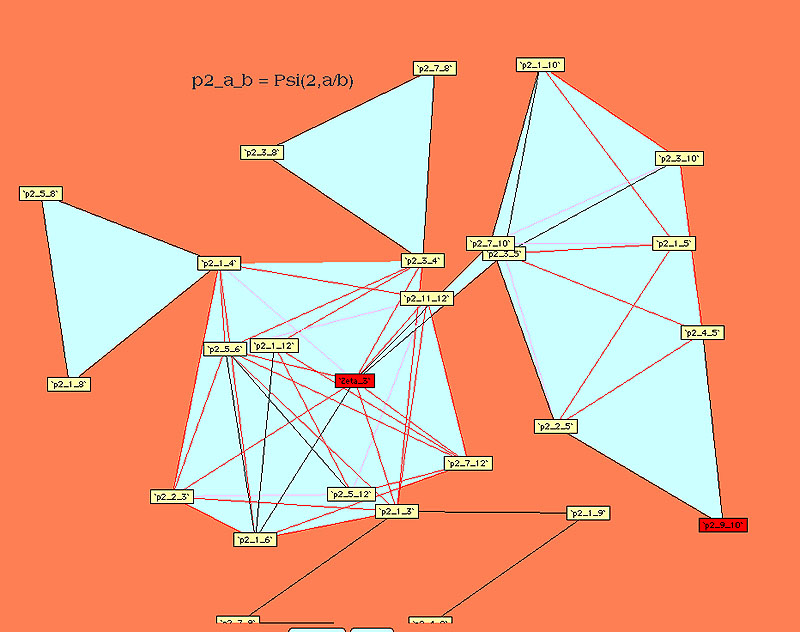
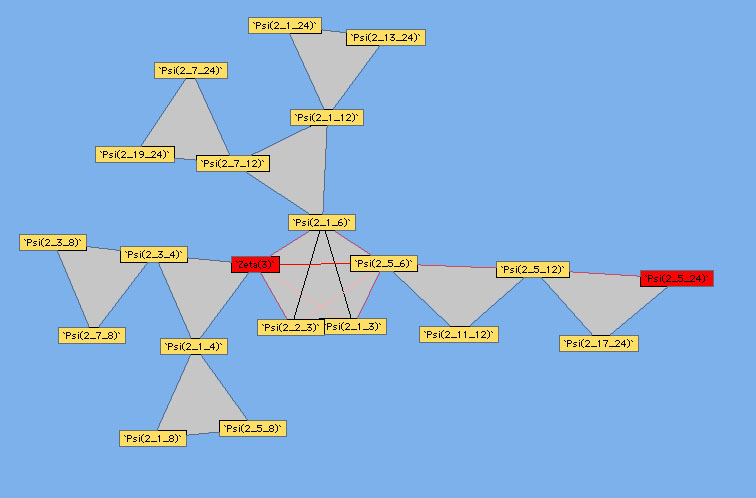
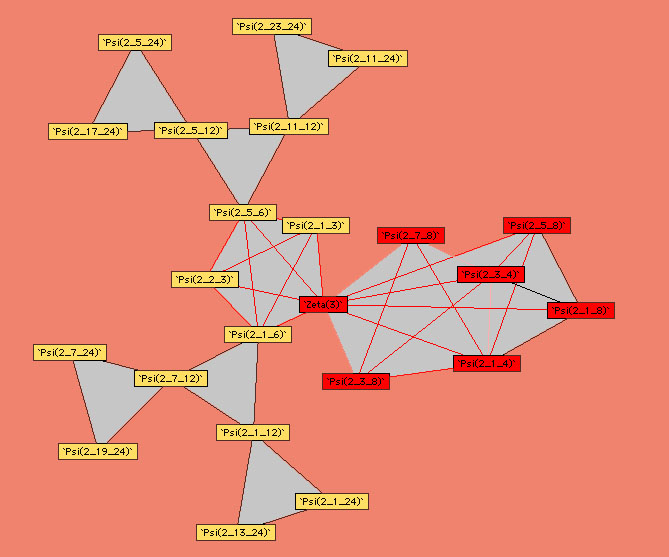
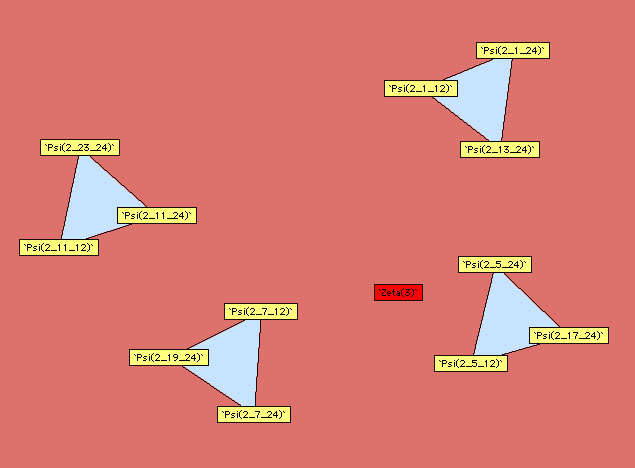
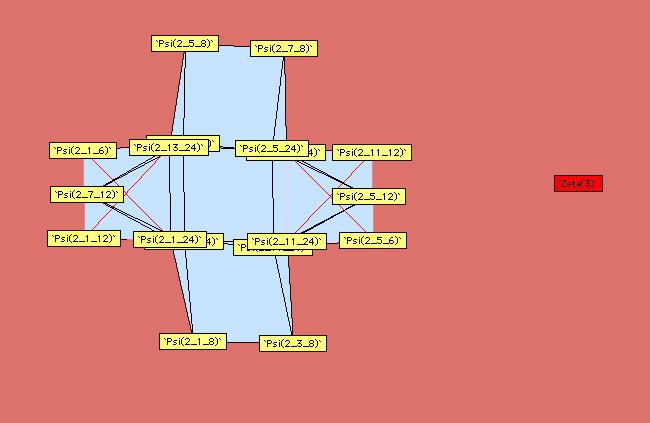
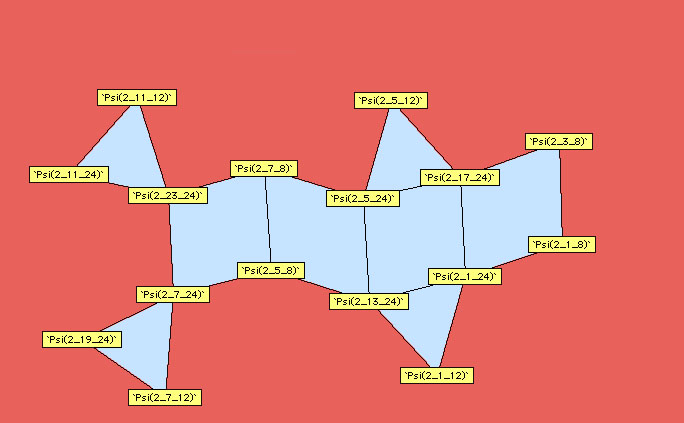
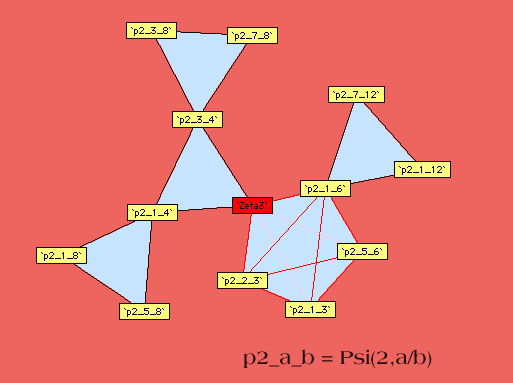
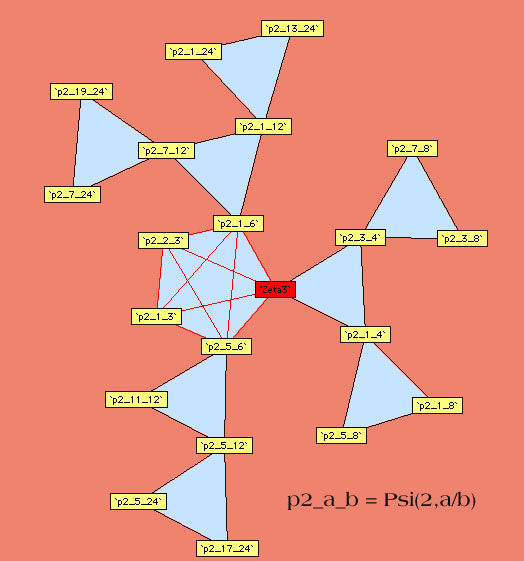
9.3.2 A graphical approach

Plouffe approached the linear relations from an other angle than that of classical formulae, it's the linear link. In fact, by systematically searching for relations for the polygamma of order 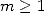taken with rationals values with some small denominators, we can constuct some schema synthetising the link between polygamma of the same order. We just need to follow the path of the line to observe which constant are linearly link between them.

Concerning notation, we'll notice that the differentiation of the digamma function is the polygamma function of order 2 : 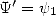to understand Plouffe's notation.

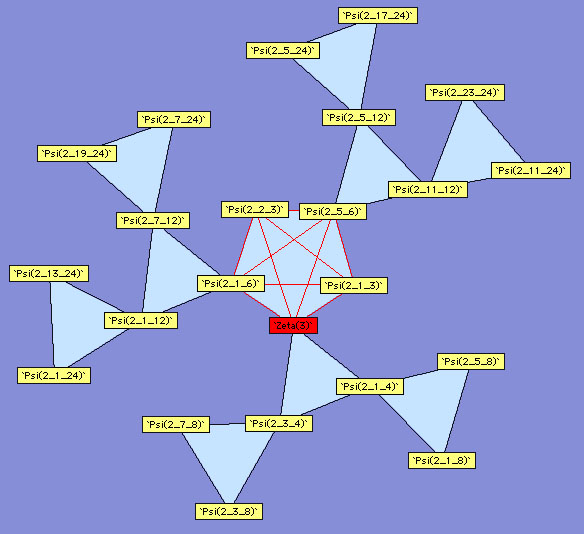
A first example is given with the constants 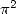and 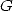(Catalan's constant) which is of order 2 as everyone knows :

Here, we need to understand that the circuit between 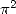, , 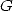and 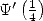is closed since they form a triangle. Hence numerically, we have in fact

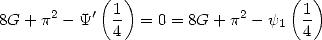(323)

As Plouffe said it, note that if we introduced 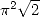, we would most likely find other diagrams of other branches of existing diagrams.

I also take his commenteries, only common sense, which indicates for example on the diagram we can not apparently find relations in 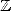between 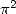, , 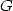and 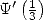, but nothing say about it's validity in other domains, in fact with 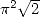or other things of the kind.

The symetry that appears in this scheme (and sometime others) is often due to analytical formula of symetry, here for example, we have

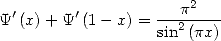(324)

which gives a lot of rational relations at least for .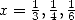

Finaly, a few liasion between rationals polygamma without 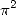or are not recopied here, so to avoid some confusions in the diagrams.

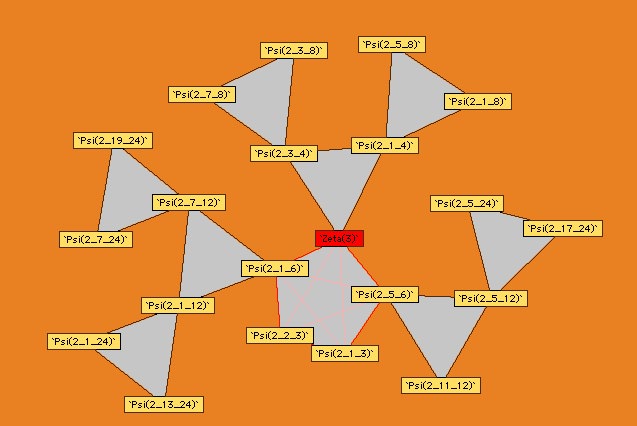
Here are the other diagrams build by Plouffe  :

Order 2

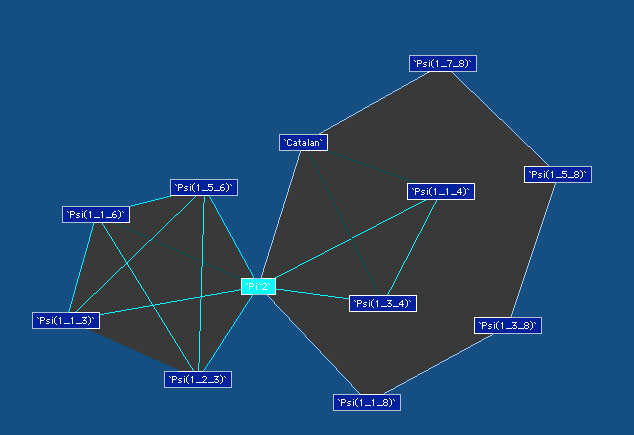
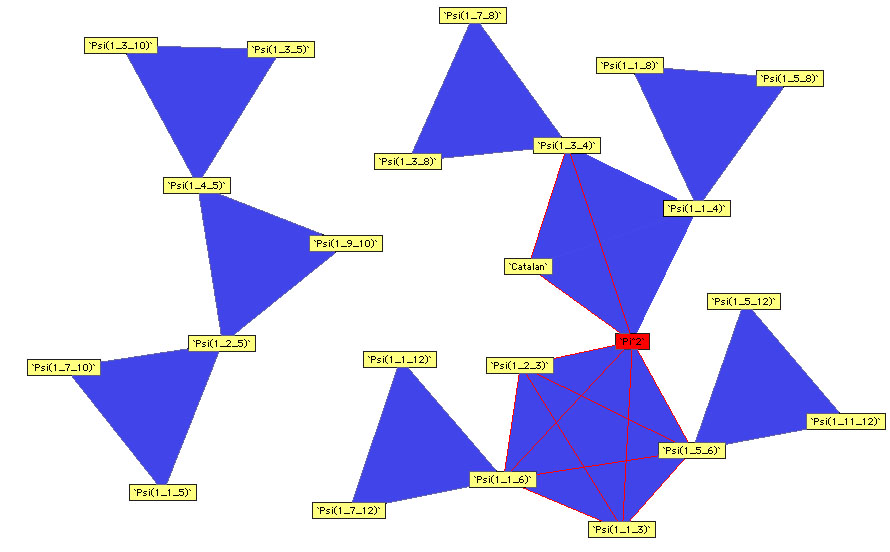
Ordre 3

9.3.3 Analytical translation 

Here are a few example of relation, where we see even the dilogarithm appear! We can find the set of relations discovered by Plouffe on this page and surf through the sections dedicated to Euler's gamma constant, or 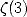, etc...

Order 2

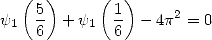(325)

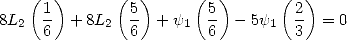(326)

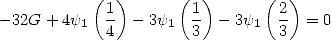(327)

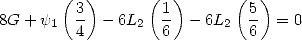(328)

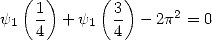(329)

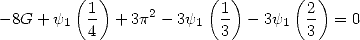(330)

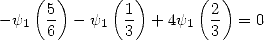(331)

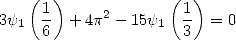(332)

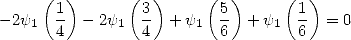(333)

Order 3

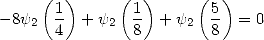(334)

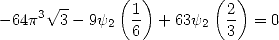(335)

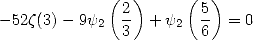(336)

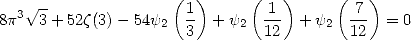
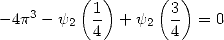
among others...

Proof Here is the proof af a formula, for example :

The most well know must be

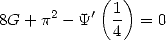(337)

Proof. The proof here uses the serie and the integral representation. We can already note that 

according to the equivalent integral form (see 322), or in equivalent serie

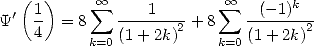(339)

The right hand side is the definition of Catalan's constant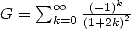. For the lest hand side, two option are possible, we can either go through the integral forms to find well known dilogarithms

We can also see all of this more directly by manipulating Euler's serie

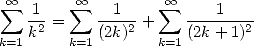(341)

by cutting the serie among the even and the odd, i.e.

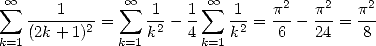(342)

From here, we have 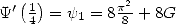and the said relation _

This kind of easy but characteristic is found in all relations of this section. We mess around with the serie, or we go back to the integrals (or a mixture of the two). It's often easier than for the BBP formulae strictly speaking because the cconsidered integral is always between 0 and 1 (in it's usual form)

9.4 Kölbig's combination

A powerful approach comes from a promotor article by K.S. Kölbig [15] who puts in relation the polygamma and Clausen functions. A little demonstration needs to be done !

9.4.1 Clausen's Functions

Clausen's functions are defined by series which already seems interesting !

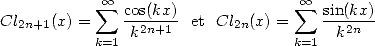(343)

We have in fact straight away

The asymetry of the definition (why not consider 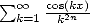 ?) comes from the fact that for opposite parities, the formulae can only be calculated explicitely by diverse classical method of integration and analysisp... For example, we have

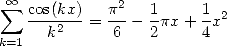(345)

or even

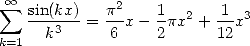(346)

It's a lovely mathematical problem to understand why it does not work so well in both cases! It's a similar problems to the one that concern the odd and even values of Riemann's function .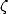

A classical result (since there exist some !) is that

(347)

which is a good way to link those two constants !

Clausen's functions are know that they can be express in functions of known constant uniquely for a little number of the value of . Which is not very interesting normaly... But we are going to see that by using the polygamma functions, we can sometime links them to something else !

9.4.2 Kölbig's results.

Introduction To come to Kölbig's result, we can first of all notce that an integration gives

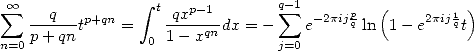(348)

by decompostition of the fraction in simpler elements. The relation is valid for 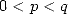. It's an other way to look at the BBP formulae, without no interest since in the demonstration, we are going to see for example that the nature of those constant that intervin are not determined by the coefficient 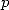, it being a simple weighting in front of the logarithm. It is said that the relation is thanks to Jensen and can be found by developing the logarithm ! Me, I don;t see where the difficulty was by passing through the decomposition in simple elements, but I could be wrong ?

Then, the continuity relation by Abel allows to write that for the digamma function,

There we go.

Greater Orders In fact, Kölbig obtained very similar result, but on the differentiation on the digamma function, which we know are the polygamma. Instead of having some logarithm, we have some polylogarithm (logical!) and instead of a logarithm function of the complex exponential, we have polylog of the complex exponential, which we just know are Clausen's function according to 344 ! All of this is very coherant and gives the following Kölbig's relation

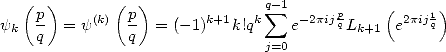(350)

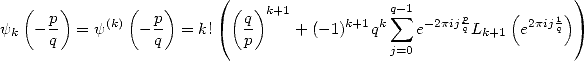(351)

which is directly proven by the definition of polylogarithm by summing on  :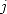

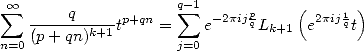(352)

We can notice that we obtain the famous multiplication formula for the polylogarithm by letting 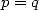in this equation, it's nice !

I won't go into the details of the nine page long proof in Kölbig's article by the principle is the following: Since the left hand side is real, we taje the real part of the right hand side and we calculate the differentiation of what appears. By considering the general inverse relation, and by using the fact that

(353)

for 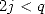, we finaly obtain that

Theorem 15 of Kölbig

For , ,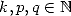

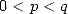and the even orders, for , ,

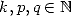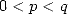where 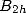is the number of Bernoulli's indice .

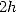Some applications Above (342), we have showed that

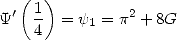(356)

but we can also note that we have

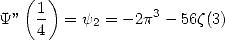(357)

which allows us to obtain the values for 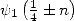and 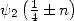from the recursion formulae

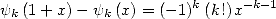(358)

and with some thinking

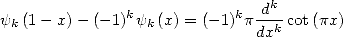(359)

but the main interest in those formulae is to give some values for 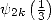, , 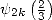, 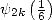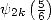in function of well known constants ! For ,

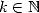We hence find the relations (325), (331), (332), (335) and (336) given by Plouffe .