1 A small quick historical recap

The Machin  formulae, and even the ones by Plouffe are special case of hypergeometric series (but it is true that they are not the most interesting, the one that take more advantage of the structure of an hypergeometric serie). Hypergeometric series interested many mathematician during the 19th century but they were hard to study theoreticaly due to the variaty of their form. A lot of result concerning more the relation between famillies of hypergeometric series such as the 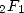. Passionated by those series, Ramanujan left us numerous relation and  formulae which seems to lead us to extraordinary ends! But there was still a lot to do.... even simplet things! Let us go back a bit....

After the Bailey-Borwein-Plouffe serie in 1995, we could think that numerous similar result would appear quickly, but after Bellard formula in 1997, the enthousiasm seem to have fallen back down because mathematicians were blocked by the impossibility to find a formula in base 10 for Pi. An clever algorithm by Plouffe and an improvement by Fabrice Bellard allowed to calculate any decimal of Pi without knowing the previous one, but the speed and the simplicity were not the same... They therefore turn more and more towards a way to exploit those results to proof the normality of Pi. What is more beautiful than a formula giving a way to simply calculate any digit of Pi or a logarithm in base 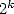without knowing the previous one, so to study the spread of those digits? The intuition was good and David Bailey with Richard Crandall seemed close to a result even though a difficult conjecture still needs to be resolve (see article [11]).

But concerning the formulae, only David Broadhurst [3] seems to be continuing the exploration since 1998, underligning more and more links with the representation of BBP formulae and with the "ladders" of polylogarithm and Kummer equivalence (when he does not put in evidance the apperance of polylogarithms in the physics of Feynman diagrams!) I have found in 2000 some BBP formula for Zêta(3) (proved) and for Catalan's constant, which seems to figure inmplicitly in Broadhurst's article, but nothing is sure... Gery Huvent (with whom I talk nearly every day during certain periods!) realise in 2000 and 2001 [12] a systematic theoretical exploration of the first order of BBP series, with classical tools of analysis, which unify a lot of things remarquably. Obviously, the more we increase in order (in multiplicative combination of constants), more the results are harder to obtain but still interesting anyway...

Gery deserveto have his page on this site, for his mathematical quality and because our discussion give me a lot. Allying my explorative enthousiasm with his fertile ideas, I find that we have each well progress in our understanding of this domain, even if certain theoretical ddevelopment of Broadhurst or his recent article are very impressive. Those pages are therefore a little hommage to Gery Huvent , who wrote lets say a good half of what you will read in those pages.

And taking the relay of BBP formulae, which now seems more understood, factorial formula, with combination, direct application of hypergeometric series, take the relay! 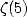William Gosper has open the way as well as the famous Comtet in 1974 for example, but it's thanks to the study of a few family of integrals, that we understand more and more series of this kind and give answers to some question that poisoned the intuition of many specialist during several years (for example why could we not find a simple relation between and ...).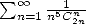

Gery Huvent explores yet once more the domaine in 2001 and on my own I discover numerous factorial formulae that I thought were new but were published here two month later in an article ( [7]) which explain the fundamental of the discovery of this kind of formula... I complete this article with an exploration of BBP binomial formulaes and the method of the Bêta function, with Jesus Guillera, who generalise in a certain way the BBP formula [13] and who try to unify the writing of series in BBP form.

The series with harmonic coefficient are equally an interesting domain, who'se link with the BBP formula is clear thanks to the integral representation of the generating formula of harmonic sums. On the other hand, the series with harmonic coefficient are not hypergeometric series (to my knowledge...), but deserve to appear here due to their very similar cute results!

All of this in the hypergeometric series fram that I will present first of all so to fix the idea of series... Note that the federator element of all those formulae is the equivalent integral representation, whose simplified form will always be of the kind

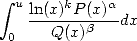
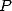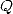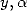where and are polynomilas on , and 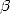are rationals. However, apart from the proof, I will not structure the work around those particular case of integrals, first of all because historically, it's not what came first, and also the series have traditionally a real calculating or theoretical interest, like the BBP formulae, which an integral can not boast of, even if it is equivalent to the serie! The problem of integrals is that they don't say straight away what they will give as a result.... Finnaly, the hypergeometric series have a name, while this kind of integral doesn't to my knowledge...

Om this page, I will take in detail the points mentioned below, with other classical mathematical series, by comparing them with hypergeometric series or the integrals, so to give you a more precise point of you on this very very fertile domain that is currently explored!

If you are not familiar with hypergeometric notations, I will strongly advise you to read the introduction to hypergeometric series page.

One more thing, the "intellectual property" of all those series is often hard to rebuild. Certain series are simple and well known since this kind of integral were manipulated, but with no precise referance, while other have few chances to be met. I will try often to precise next to the formula who showed it to me first, so to say directly, but if you have a older reference, don't hesitate to tell me!