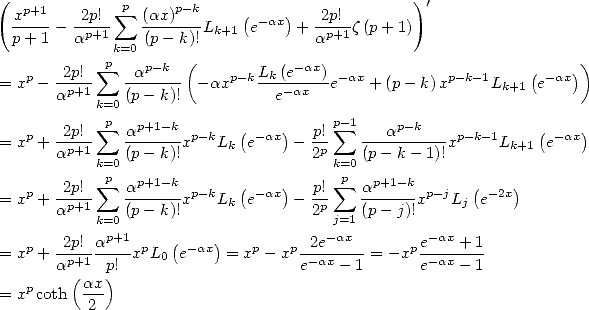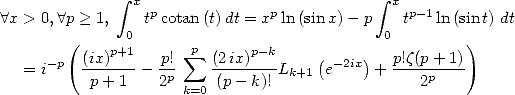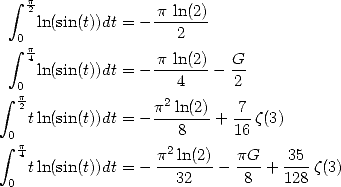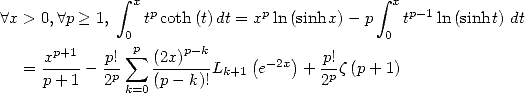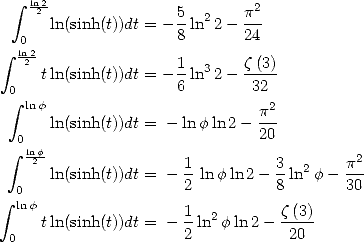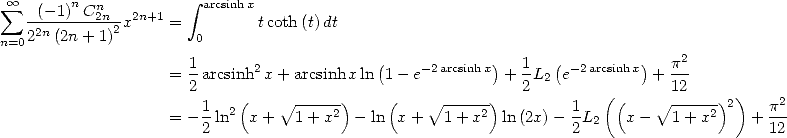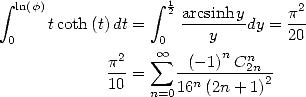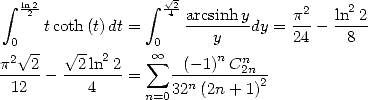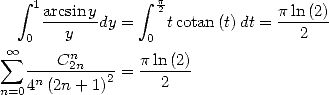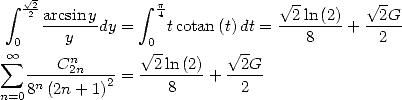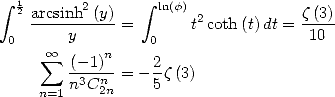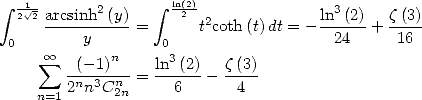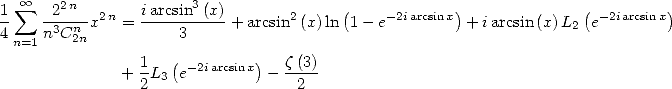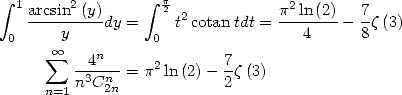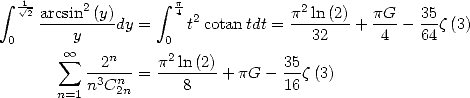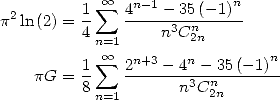|
The world of Pi - V2.57 modif. 13/04/2013 |
|
|
|
11 Centrals binomial series
An interesting particular case and yet not to har on factorial series involve the introduction to the central binomials coefficients in the series. After a few notes on those series in the first section we will plunge into serious stuff with several formulae and their proofs!
11.1 Combinations inversion
A funny thing is that we can obtain some series giving the same result but in one case with the central binomial coefficient on the numerator, while in the other on the denominator! This also confirrm why we obtain the same kind of results with a serie with a combination and one without:
Let us take the example of the 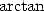 function: first of all, we have the
classical formula
function: first of all, we have the
classical formula
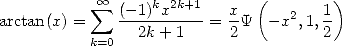 |
(372) |
We know from Euler (see Euler's page) that the arctan function can also be expressed as
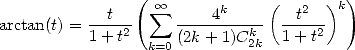 |
(373) |
Finaly, the coupled relation 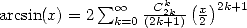 with
with 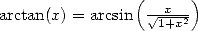 give
give
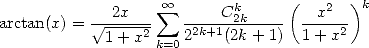 |
(374) |
A relation between the different series and the central binomial coefficients is hence the arctan :
Suprising, no ? ! !
By deriving the serie from the center along  ,
we can for example find the expression under the combination form of
,
we can for example find the expression under the combination form of 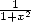 .
.
And so starting from this serie, we can find the combination expression of serie of type Machin under the form of combination of binomial formulae! We will see in the following section the 11.3factorials.
We can anyway signal for the arctan function
The proof is obvious by decomposing the serie in even and odds...
Furthermore, we also have, still playing of the developpement of power series
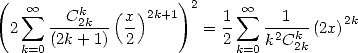 |
(378) |
Finally, we have according to the expression 13 and 11
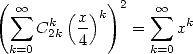 |
(379) |
which is ammusing as well !
11.2 Useful development
We remember the following development of power series which will be useful for the calculation of certain series and integrals. :
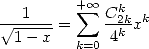 |
(380) |
which, by composing by 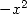 or
or 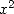 and by integrating, give respectively
and by integrating, give respectively
furthermore, Euler's developpement given under
it's 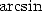 form
form 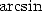
that we can hence proof by the method of differential equations.
11.3 First direct formulae
The four last developpement of the previous
section give then classical series, with 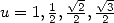
By using
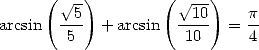 |
(389) |
we can obtain, for example
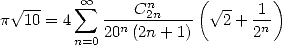 |
(390) |
With the developpement of 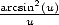 , we obtain
, we obtain
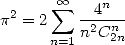 |
(391) |
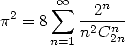 |
(392) |
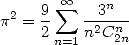 |
(393) |
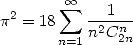 |
(Euler 1748) |
The values 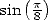 ,
, 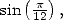
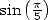 gives the formulae
gives the formulae
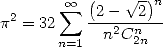 |
(394) |
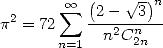 |
(Grandall 1994) |
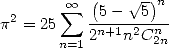 |
(395) |
We can also write that 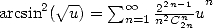 which when differentiating gives
which when differentiating gives
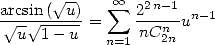 |
(396) |
and obtain pther series such as
By differentiating again 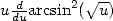 , we have
, we have
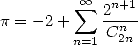 |
(400) |
etc...
On the same model, Gery Huvent offered what seems an open conjecture, having not read stuff on this subject...
11.4 Formulae of greater order
The study of series of the kind 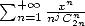 or
or 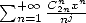 , for
, for 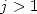 complicated things a lit, because those sums comes from succevise
integrations of functions where
complicated things a lit, because those sums comes from succevise
integrations of functions where 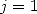 .
In fact, we will notice that
.
In fact, we will notice that
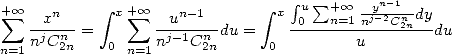 |
(407) |
and so on to go back for example up to 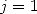 .
.
but of course, those functions don't let themself be easily integrated! And we often need to have a lot of patient and a few trick up our sleeves to see the end of it.
However, the results are there. We know Euler's formula
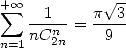 |
(408) |
who I give a proof to the paragraph dedicated to 10.2calculus and the method of convergence acceleration by the finite difference, invented by Euler himself!
The greater order, it's a formula such as
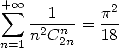 |
(409) |
but also
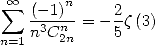 |
(410) |
and the formula by Comtet dating of 1974 whose proof was tedious...
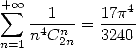 |
(411) |
Obviously, this intrigued mathematicians to
know wether a similar formula existed for order 5! Unfortunatly, we now
know that this serie does not give the wanted result since if we recall
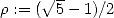 , we have according to
[8]
, we have according to
[8]
But this doesn't stop the higher order from being interesting.
11.4.1 A first formula with proof
I noticed in august 2001 that
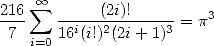 |
(413) |
which is transformed into hypergeometric form into
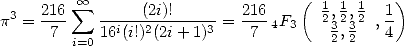
It must be one of the simplest factorial
formula and the presence of the 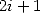 make it seems like a BBP formula. The proof is complicated and
linked to the folowing integral calculation
make it seems like a BBP formula. The proof is complicated and
linked to the folowing integral calculation
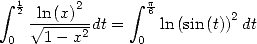 |
(414) |
because the development into power serie of 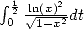 give
give
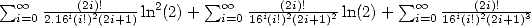 which we know how to calculate the first two part.
which we know how to calculate the first two part.
We hence let more generaly the following integrals :
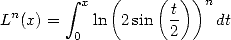 |
(415) |
Note that we can clearly brings this integral
back to 9.4.1in
the sense where 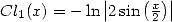 and
hence
and
hence
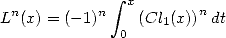
for 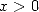 .
There no coincidence !
.
There no coincidence !
The result that interest us is
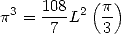
which is equivalent to the serie through an
immediate change of variable 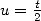 in 414.
in 414.
Raymon Manzoni, then Gery Huvent , contributed to give a proof for this formula, which I will present to you now, and also including a proof of the formula by Comtet done by Gery Huvent .
Proof. Consider,
for integers 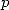 and
and 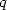
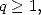 the function
the function
this function is holomorph on
For ![p = 0, C\]1,+ oo [](../mathematiciens/huvent/hyperg1180x.gif)
For 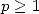
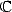 without
without ![]1,+o o [](../mathematiciens/huvent/hyperg1183x.gif) and de
and de ![]- oo , 0]](../mathematiciens/huvent/hyperg1184x.gif)
Consider, for ![x (- [-p,p]](../mathematiciens/huvent/hyperg1185x.gif) the path
the path ![g(t) = eit, t (- [0,x]](../mathematiciens/huvent/hyperg1186x.gif) and the integral
and the integral 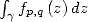 (with
(with 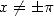 if
if 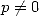 ).
).
Since 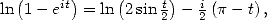 we have
we have
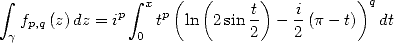 |
(417) |
If 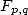 disign a primitive of
disign a primitive of 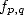 on the domain containing the path
on the domain containing the path 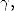 we
have
we
have
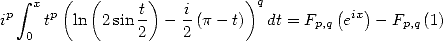 |
(418) |
The problem hence goes back to the calculation
of a primitive !
The null primitive of 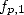 in
in  is
is
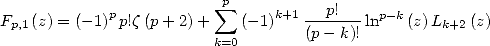 |
(419) |
Hence
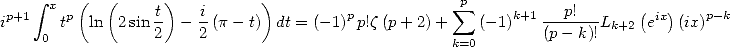
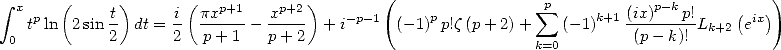 |
(420) |
We therefore obtain a second expression of 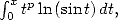 by comparing with it
what we already obtained, for
by comparing with it
what we already obtained, for 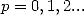 , we find again simply the value of
, we find again simply the value of 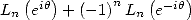 . This is nothing new,
because we know the developpement in Fourier siries of the nth
polynomial of bernoullli. This developpement gives the equality
. This is nothing new,
because we know the developpement in Fourier siries of the nth
polynomial of bernoullli. This developpement gives the equality
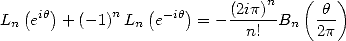 |
(421) |
The primitive of 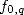 which is nul in
which is nul in  is
is
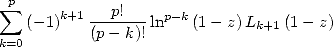 |
(422) |
hence
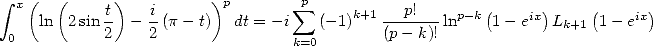 |
(423) |
In particular,
We can refind that 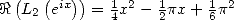 and that
and that
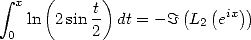 |
(425) |
And
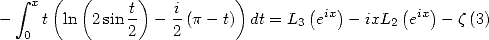 |
(426) |
from which
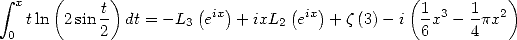 |
(427) |
Then we have
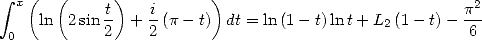 |
(428) |
which allows us to find Euler's formula for the dilogarithm
hence
Note 22 We can simplify this equality with Landen's formulae and find the classical result
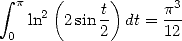 |
(431) |
result that we obtain with the developpement into
Fourier's series of 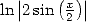 and
Parseval's formula.
and
Parseval's formula.
in particular
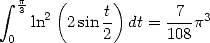 |
(Gourevitch) |
because
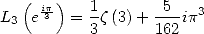 |
(432) |
This equality then gives with 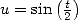 and a DSE
and a DSE
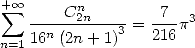 |
(Gourevitch) |
We can also establish that
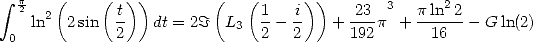 |
(433) |
We can also calculate the primitive of 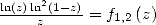 , we find
, we find
This equality allows several applications :
The equality
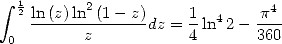 |
(435) |
Then with
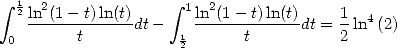 |
(436) |
obtained by integration by parts and changing
variables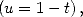 because
because 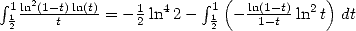 .
.
We have
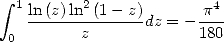 |
(437) |
which gives
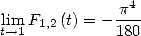 |
(438) |
Finnaly, starting from
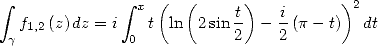 |
(439) |
that we developpe like in the previous example, we find
With 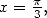 and taking into account the value of
and taking into account the value of 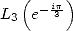
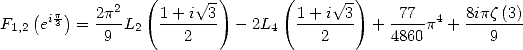 |
(440) |
which gives
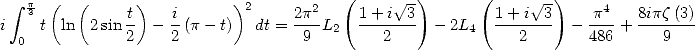 |
(441) |
By developping the square under the integral and
by taking into account the previous calculated values of 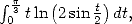 it
turns out (Oh miracle!) that we get
it
turns out (Oh miracle!) that we get
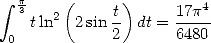 |
(Comtet) |
This last equality, gives with 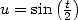 and the DSE of
and the DSE of 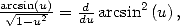 the
equality
the
equality
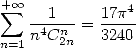 |
(442) |
With 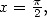 the result is less simple, however we have
the result is less simple, however we have
By combining with 433, we have
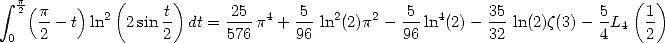 |
(444) |
_
Now the trick is to use this approach to developpe a particular method and as often we need to go through equivalent integrals, who we just saw a first example. All of this on an idea by Gery Huvent :
11.4.2
Calculation of a primitive of 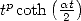
For 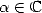 , we introduce the function
, we introduce the function
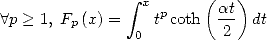 |
(445) |
Proof. We differentiate the right hand side,
Then in 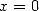 the right hand side is equal to
the right hand side is equal to  .
_
.
_
Application :Intégrales of
kind Dirichlet Consider the equality (446) with 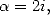 we obtain the expression of the integral
we obtain the expression of the integral 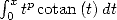 with the help of
polygarithms. An integration by part (where we integrate the cotangent)
gives
with the help of
polygarithms. An integration by part (where we integrate the cotangent)
gives
We then obtain the following equalities
With 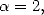 we
get
we
get
which gives
For the folks mathematics We then easily show that
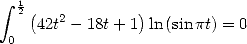 |
(459) |
The minimum of the trinomial 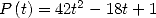 is obtain in
is obtain in 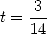 , funny !
, funny !
11.4.3
Uses of 
Uses of the primitive for 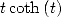 We have for
We have for 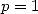 and
and 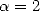
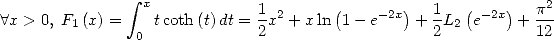 |
(460) |
Hence for 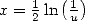 or
or ![u (- ]0,1[,](../mathematiciens/huvent/hyperg1273x.gif) we obtain
we obtain
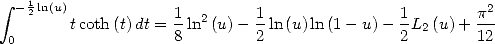 |
(461) |
Starting from
![integral x sum oo n n
A x (- [0,1], arcsinhy-dy = -(--1)-C2n-x2n+1
0 y n=022n(2n+ 1)2](../mathematiciens/huvent/hyperg1275x.gif) |
(462) |
The change of variable 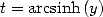 then gives
then gives
As an application, we obtain for 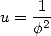
As another application, 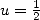 gives
gives
Uses of the primitive of 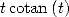 We have for
We have for 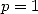 and
and 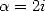
![] [ integral x 2 ( ) ( ) 2
A x (- - p, p , tcotan(t)dt = ix-+ x ln 1 - e- 2ix + i L2 e-2ix - ip--
2 2 0 2 2 12](../mathematiciens/huvent/hyperg1285x.gif) |
(466) |
Starting from
![integral x oo sum n
A x (- [0,1], arcsin-ydy = ---C-2n----x2n+1
0 y n=0 22n (2n + 1)2](../mathematiciens/huvent/hyperg1286x.gif) |
(467) |
the change of variabl 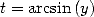 gives
gives
![oo sum ---Cn2n---- 2n+1 iarcsin2x- ( - 2iarcsinx) i ( -2iarcsinx) ip2
A x (- [0,1], 22n (2n + 1)2x = 2 + arcsinx ln 1 - e + 2L2 e - 12
n=0](../mathematiciens/huvent/hyperg1288x.gif) |
(468) |
As an application, we have with 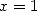
With 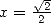
11.4.4
Uses of 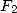
Uses for the primitive of 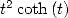 We have for
We have for 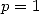 and
and 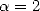
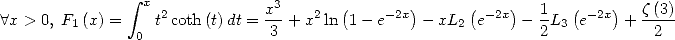 |
(471) |
Starting from
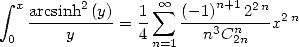 |
(472) |
by change of variables, we obtain ![A x (- [0,1],](../mathematiciens/huvent/hyperg1299x.gif)
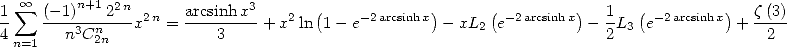 |
(473) |
With 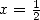 , we get
, we get
It's with this last equality that Apery proved
the irrationality of 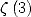 .
.
With 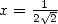 we have
we have
Uses of the primitive of  By the same kind of method we obtain
By the same kind of method we obtain
which with 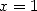 gives
gives
then with 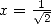
By combining those last two equalities with the one found by Apéry (474), we get
11.4.5 Other formulae
Starting from the result 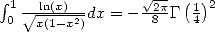 stated in the Gradshteyn [9] (4.241), we get the
formula
stated in the Gradshteyn [9] (4.241), we get the
formula
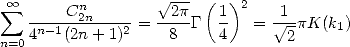 |
(484) |
Nice formula, putting in evidence the arrival of a constant linked to elliptical integral of first sort, not bad...
back to home page

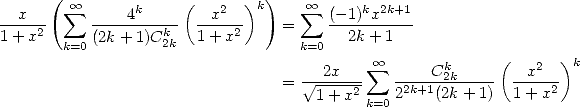
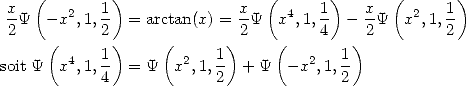
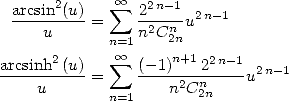
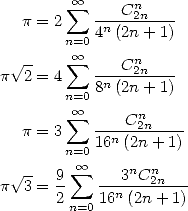
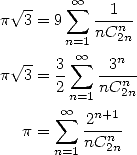
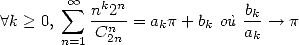
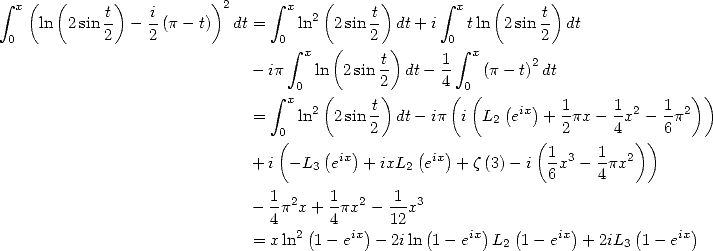
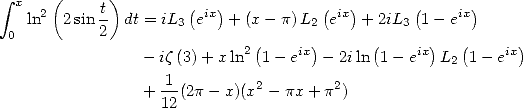
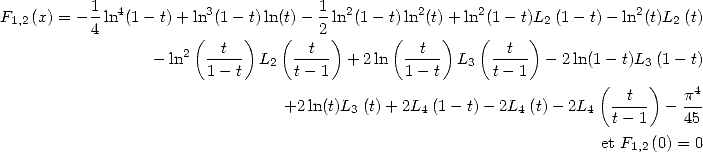
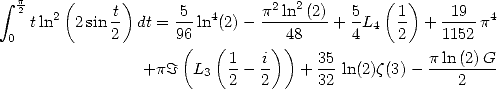
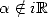
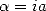
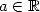
![] p p [
- a,a.](../mathematiciens/huvent/hyperg1253x.gif)