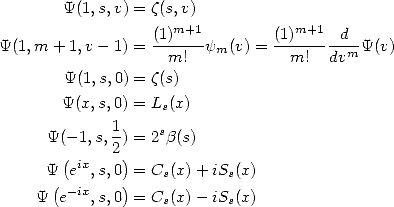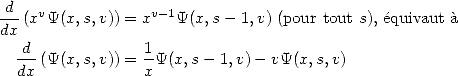|
The world of Pi - V2.57 modif. 13/04/2013 |
|
|
|
3 The Psi function: The basis to formulae of type Machin or BBP
3.1 Definition
We want to be able to combine in a 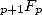 serie the combination and the terms
serie the combination and the terms 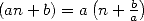 . For this we
will introduce the Psi function, or Lerch's transcendance, which is
written
. For this we
will introduce the Psi function, or Lerch's transcendance, which is
written
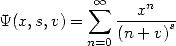 |
(16) |
for 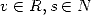 . The convergence radius is of
. The convergence radius is of 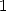 . We
can write this function in a fairly simple hypergeometric function :
. We
can write this function in a fairly simple hypergeometric function :
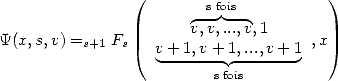 |
(17) |
This function has the advantage of regrouping a good part of classical functions of analysis, it's not that suprising since the relations between them are many!
So, we get
where 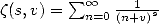 is
the Zêta function of Hurwitz,
is
the Zêta function of Hurwitz, 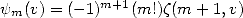 is the
PolyGamma function and
is the
PolyGamma function and
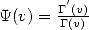 is the Digamma
function.
is the Digamma
function.
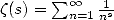 is the famous
Zêta function,
is the famous
Zêta function, 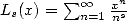 is the
polylogarithm of order s,
is the
polylogarithm of order s, 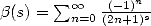 is the
Bêta function of Dirichlet, and finaly
is the
Bêta function of Dirichlet, and finaly 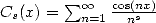 and
and
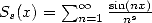 are
Clausen's functions.
are
Clausen's functions.
3.2 Differential Equations
The function 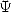 is
a hypergeometric serie, so we can fire at it any kind of differential
equation. Among all of those, let's take :
is
a hypergeometric serie, so we can fire at it any kind of differential
equation. Among all of those, let's take :
but also by iterating
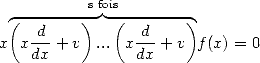 |
(26) |
back to home page