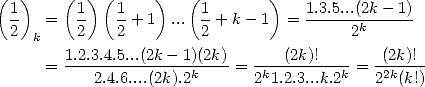|
The world of Pi - V2.57 modif. 13/04/2013 |
|
|
|
2 Introduction to hypergeometric series
2.1 Definition
An general hypergeometric function is defined by the serie
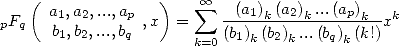 |
(1) |
where 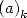 is Pochhammer's symbol and is equal to
is Pochhammer's symbol and is equal to 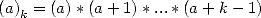
It's a generalisation of the factorial
function. A simple example of the value of Pochhammer's symbol is 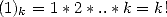
An very important example of the value of
Pochhmmer's symbol concern 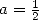 :
:
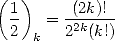 |
(2) |
In fact,
which is equivalent to 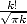 when
when 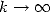 due to Stirling's equivalence, so you
have an idea.
due to Stirling's equivalence, so you
have an idea.
In truth, we get 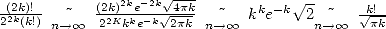 .
.
In fact, there is a simple way to check if a
serie can be put under a hypergeometric serie form. For this we
calculate the ratio 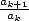 and we try to put it under the form
and we try to put it under the form
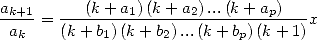 |
(4) |
that is a polynomial ratio in 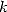 .
Under this form, we can then precise that
.
Under this form, we can then precise that
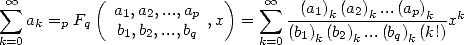 |
(5) |
Generally, for the series that don't give any simple results, we can often go back to study an integral involving the logarithm to the numerator (eventually at a certain power) and of the polynomials (eventually at a certain non integer power) i.e.
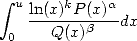 |
(6) |
2.2 A few properties and simple examples
The ratio between 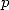 and
and
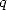 is very important so to known toward which kind of
result we are going to. Because the result of a hypergeometric series
with a fixed difference
is very important so to known toward which kind of
result we are going to. Because the result of a hypergeometric series
with a fixed difference 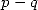 are ”homogenous”, that is the closed
form are always combinations of the same kind of basic function. (Of
course, the combination can be very complicated, but it is important
that we always see the same basic function appearing)
are ”homogenous”, that is the closed
form are always combinations of the same kind of basic function. (Of
course, the combination can be very complicated, but it is important
that we always see the same basic function appearing)
For example, the simple example
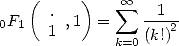 |
(7) |
leads the result of the series 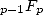 toward Bessel's function :
toward Bessel's function :
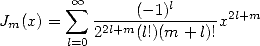 |
(8) |
for Bessel's function of first sort for
example (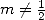 ), while the other serie
), while the other serie
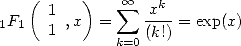 |
(9) |
indicates the variation of the coefficients for
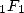 (and more generally
(and more generally 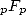 )
give us functions based on the exponentianal function. This, as we have
often seen, does not linearly join with
)
give us functions based on the exponentianal function. This, as we have
often seen, does not linearly join with 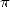 in
the sense that one does not find in nature a natural serie which give
for example a result of
in
the sense that one does not find in nature a natural serie which give
for example a result of 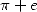 unless you add two series who do not have
the same form and each converges towards one of the two constants !
unless you add two series who do not have
the same form and each converges towards one of the two constants !
I don't know the result for the series 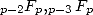 ... but we can see that we are adding then factorials to
the denominator and so we have few chances of finding anything but
exotic functions that are impossible to write under simple form!
There's already Bessel's function..... Furthermore, they are all close
to functions that satisfy similar property to the exponential function.
... but we can see that we are adding then factorials to
the denominator and so we have few chances of finding anything but
exotic functions that are impossible to write under simple form!
There's already Bessel's function..... Furthermore, they are all close
to functions that satisfy similar property to the exponential function.
Notice that in all cases with factorials on the
denominator for series of type 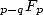 with
with 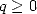 , we have a great convergence radius of infinity,, which
is nice.... but we already knew it for the exponential function.
, we have a great convergence radius of infinity,, which
is nice.... but we already knew it for the exponential function.
If we taje a coefficient to great compare to 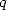 ,
the series are less interesting to calculate because they don't
converge. For example the serie
,
the series are less interesting to calculate because they don't
converge. For example the serie
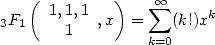 |
(10) |
has a convergence radius of zero, that is for
any fix number no mater how small it is, the serie won't converge. The
factorial is too powerful! It increases to fast compared to 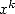 ...
It's also the case generally for the series
...
It's also the case generally for the series 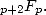
This leave us with the intermediate case
represented by the function 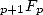 who gave us numerous result in the last two century. This is principly
due to the fact that the series are homogenuous often to combinations
of radicals of polynomials of kind
who gave us numerous result in the last two century. This is principly
due to the fact that the series are homogenuous often to combinations
of radicals of polynomials of kind 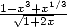 or integrals with this
kind of things (and in particular the whole class of elliptical
integrals). And this is good for us, because we know with this kind of
integral we enter completly into the class of integrals which give us
some
or integrals with this
kind of things (and in particular the whole class of elliptical
integrals). And this is good for us, because we know with this kind of
integral we enter completly into the class of integrals which give us
some 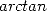 and
and 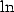 , hence
, hence 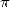 ! !
! !
The simplest example must be
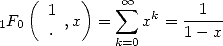 |
(11) |
but we can also interest ourself to the Newton's general binomial formula with rational powers and note that
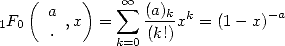 |
(12) |
which gives us for example
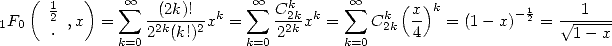 |
(13) |
We see here appear some combinations  whose factorials do their bit to be
into hypergeometric serie form. The series of type
whose factorials do their bit to be
into hypergeometric serie form. The series of type 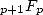 have a convergence radius between infinity of the series
have a convergence radius between infinity of the series 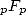 and the zero of the series
and the zero of the series 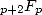 i.e. naturally 1 ! We can
convince ourself by taking the ratio of the terms of the serie
i.e. naturally 1 ! We can
convince ourself by taking the ratio of the terms of the serie
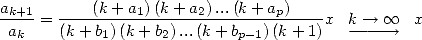 |
(14) |
Acording to Alembert's rule, the limit of those
ratio is the inverse of the radius of convergence multiplied by  , so
here this radius is
1.
, so
here this radius is
1.
The derivative of a hypergeometric serie give another hypergeometic serie as the following formula illustrate
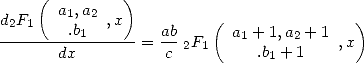 |
(15) |
The hypegeometric series are solutions to
differential equation of order 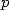 (using the differential of order
(using the differential of order 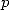 ),
the above example was just a firt illustration. This property sometimes
make the calculation of certain hypergeometric series hard, who are
equal to very annoying integrals, or even when we don't really know
which integral represent it! Those a bit too many functions quickly
interested mathematicians who found clever trick to make algorithm to
allow indirect calculation of certain hypergeometric series. One of the
first method was by Sister
Céline , then one by Gosper
(yes, yet him again! ! !) and finaly it ended with the
algorithm by Wilf-Zeilberger
whose method, while not very complicated, is a bit hard and long to
explain here...
),
the above example was just a firt illustration. This property sometimes
make the calculation of certain hypergeometric series hard, who are
equal to very annoying integrals, or even when we don't really know
which integral represent it! Those a bit too many functions quickly
interested mathematicians who found clever trick to make algorithm to
allow indirect calculation of certain hypergeometric series. One of the
first method was by Sister
Céline , then one by Gosper
(yes, yet him again! ! !) and finaly it ended with the
algorithm by Wilf-Zeilberger
whose method, while not very complicated, is a bit hard and long to
explain here...
Many are the hypergeometric function, surely! Imagine that certain very simple and well known series are particular case of them. For example we have seen appear in the formula 12 and 11 powers and combinations. We can also notice that a serie like the one by Leibniz-Gregory is written under a hypergeometric serie form :
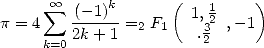 |
(Leibniz-Gregory) |
which leave us to think that all series
involving only 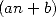 terms can also be written under the form
of hypergeometric series with the corresponding parameter
terms can also be written under the form
of hypergeometric series with the corresponding parameter 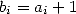 (in the above example,
(in the above example, 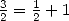 .)
.)
back to home page