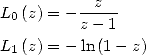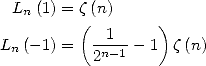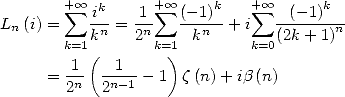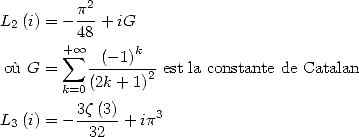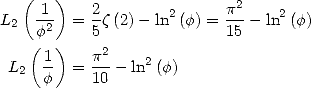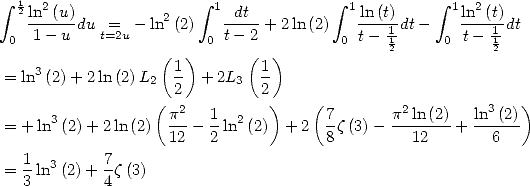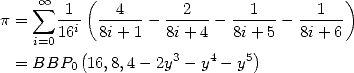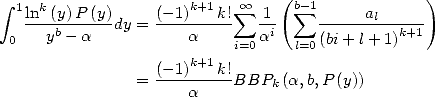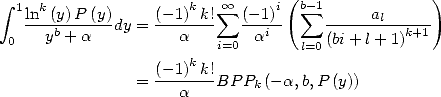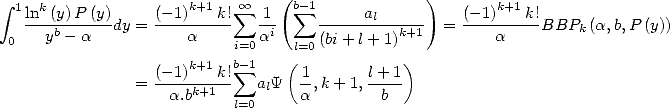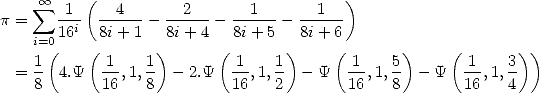|
The world of Pi - V2.57 modif. 13/04/2013 |
|
|
|
5 Formulae BBP : The technique
In 1995, Bailey, Borwein and Plouffe discovered the famous formula
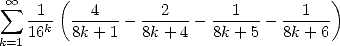 |
(B.B.P.) |
which , as we now know, goes further than it's simple form by giving us a method to find the n-th digit of Pi without knowing the previous one. Even better, it revolutionised the view of Pi by putting it amoung the constants that we can generate nearly like a chaotic dynamic system, which Bailey and Crandall turn into their famous conjecture in 2000 [11] linking the concept of normality to the passage of a digit to the next.
And with the function 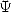 ,
quickly, we will notice that the BBP formulae are a particular case of
relations of function class that we call polylogarithms. A nice
introduction to those extraordinarly simple but promising function is
the work of e Gery Huvent that I adapt here :
,
quickly, we will notice that the BBP formulae are a particular case of
relations of function class that we call polylogarithms. A nice
introduction to those extraordinarly simple but promising function is
the work of e Gery Huvent that I adapt here :
5.1 
 : The
polylogarithmes
: The
polylogarithmes
5.1.1 Definition
For 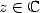 ,
,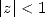 and
and 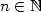 , we define the polylogarithm of order
, we define the polylogarithm of order 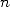 by
by
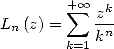 |
(32) |
Hence
For 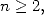 note
that the convergence is normal of the closed unity disc.
note
that the convergence is normal of the closed unity disc.
We have the following integral representation
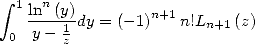 |
(35) |
which allow us to extend the polylogarithm, for 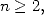 on
on ![C\]1,+ oo [](../mathematiciens/huvent/hyperg190x.gif) to a holomorphe function.
to a holomorphe function.
The polylogarithm can be also defined by succesive integration, in fact
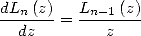 |
(36) |
as well
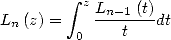 |
(37) |
and for example
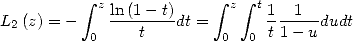 |
(38) |
5.1.2 Remarquable values
The first remarquable values are, for 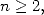
where 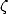 is
Riemann's zéta function
is
Riemann's zéta function
In particular
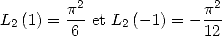 |
(Euler) |
For 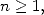
where 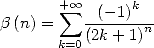 . In particular
. In particular
Note
1 We
know the exact value of 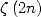 and of
and of 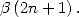
5.1.3 Duplication formula
On we have ![C\]1,+o o [](../mathematiciens/huvent/hyperg206x.gif) ,
, 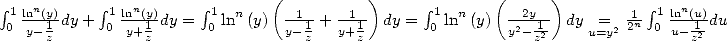 . Which prove the duplication formula, that when the
three terms have a direction :
. Which prove the duplication formula, that when the
three terms have a direction :
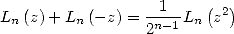 |
(45) |
5.1.4 Euler and Landen's formulae for the dilogarithm
Euler's Formulae On ![]- 1,1[,](../mathematiciens/huvent/hyperg209x.gif) we have
we have
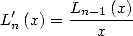 |
(46) |
This equality allow us to prove through differentiation Euler's identity for the dilogarithm
![A x (- ]0,1[, L2(x)+ L2(1 -x) = z(2)- ln (1 - x)ln (x)](../mathematiciens/huvent/hyperg211x.gif) |
(47) |
In particular with 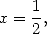 we get the following result, thanks to Euler
we get the following result, thanks to Euler
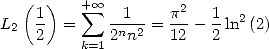 |
(Euler) |
Landen's Formulae We also have the following relation said to be Landen's identity (that we prove using differentiation)
![[ ] ( )
A x (- - 1, 1 , L2 (x)+ L2-x-- = -1 ln2(1 -x)
2 x- 1 2](../mathematiciens/huvent/hyperg214x.gif) |
(48) |
This identity is true on ![[ ]
C\RU -1, 12](../mathematiciens/huvent/hyperg215x.gif)
Particular Values
With 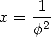 where
where 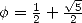 is the golden number
(which satisfies
is the golden number
(which satisfies 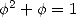 ), since
), since  in this case, we obtain
in this case, we obtain
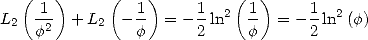 |
(49) |
But Euler's formula give us
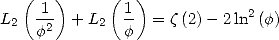 |
(50) |
and the duplication formula
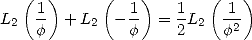 |
(51) |
By combining the three results, we get
Complex values Landen's indentity can be
extend through analysis to ![C\]1,+o o [.](../mathematiciens/huvent/hyperg224x.gif) With
With 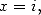 we get
we get
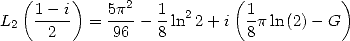 |
(54) |
5.1.5 Landen's formula for trilogarithm
![] 1]
A x (- -1, 2](../mathematiciens/huvent/hyperg227x.gif)
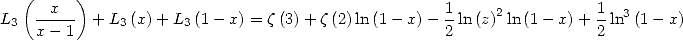 |
(55) |
This formula can be deduced by Euler's and Landen's identity for the dilogarithm after differentiation.
5.1.6 Particular values
We deduce form Landen's identity for the trilogarithm the following remarquable values :
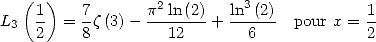 |
(56) |
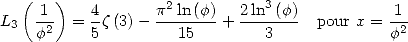 |
(57) |
5.1.7 A few classical integrals
The integral representation (35) immediatly give
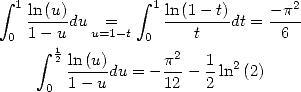 |
(58) (59) |
Similarly
5.2 The links between integrals, BBP formulae and polylogarithms
5.2.1 Notations
Let us start by simplifying notations! It would be great if we could talk about a BBP formula without having to copy down the formula every time...
Gery Huvent has
offered to denote the sum 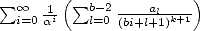 , for
, for
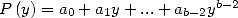 .
.
Plouffe's formula is now written
Which simplifies a lot !
5.3
Integrals and BBP formulae
In this section we offer to get integrals equivalent to BBP series. It is often the case easier to go through integral calculation to find the result of a serie!
5.3.1 Integrals equivalent to BBP series
So, from the equality 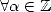 ,
, 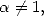 and
and 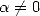 ,
,
![A y (- [0,1], A k > 1,](../mathematiciens/huvent/hyperg240x.gif)
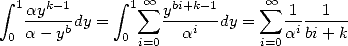 |
(62) |
we deduce that if ![b- 2
P (- Qb-2 [X] , P = a0 + a1X + ...+ ab-2X](../mathematiciens/huvent/hyperg242x.gif) then
then
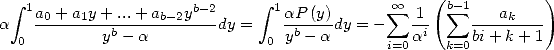 |
(63) |
Similarly,
5.3.2 More general integrals and BBP formulae
Now, we have suspicion that it is not this
kind of integrals that we would be able to calculate, and so we will
not be able to deduce BBP formula, but we should deal with an integral
of type 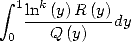 . But
the whole trick is there !
. But
the whole trick is there !
In fact, if 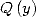 divides
divides 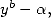
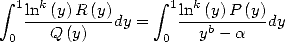 where
where 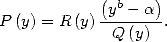 This allows, when we know how to calculate the integral
This allows, when we know how to calculate the integral 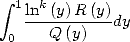 , to
deduce a BBP formula. The same kind of remarque is applicable if
, to
deduce a BBP formula. The same kind of remarque is applicable if 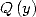 divides
divides
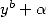 .
.
5.3.3 Calculations of intergrals
Now, lets talk about polylogarithms. The
above remarque is true in the case where 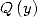 divides
divides 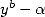 to extract BBP series. But to calculate the integral?
Well we can use a decomposition into simple elements of
to extract BBP series. But to calculate the integral?
Well we can use a decomposition into simple elements of 
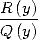 so to go back to known integrals.
And that's where polylogarithms come in handy.
so to go back to known integrals.
And that's where polylogarithms come in handy.
We remember that the integral expression of a
polylogarithm of order 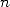 for a non zero complex
for a non zero complex  with modulus less than
with modulus less than
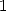 .
.
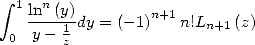 |
(68) |
This allows, after decomposition into simple
elements of 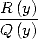 , to express an integral of type
, to express an integral of type 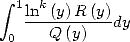 as
sums of polylogarithms.
as
sums of polylogarithms.
5.4 Function
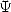 and polylogarithm
and polylogarithm
As well as the obvious relation 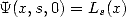 , the previous paragraph puts light to the decomposition
of a rational fraction in the integrals allows to bring BBP formula to
polylogarithm. But furthermore, the formula (64),
which we have seen the direct link to the BBP formulae if we have a
polynomial
, the previous paragraph puts light to the decomposition
of a rational fraction in the integrals allows to bring BBP formula to
polylogarithm. But furthermore, the formula (64),
which we have seen the direct link to the BBP formulae if we have a
polynomial 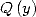 dividing
dividing 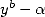 , can also be written
, can also be written
that is in the form of combination of the
functions 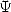 . In fact, the BBP formulae are nothing other than the
combination of functions
. In fact, the BBP formulae are nothing other than the
combination of functions 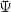 where the parameter
where the parameter  does not move and is the inverse power of an
integer.
does not move and is the inverse power of an
integer.
Hence, the Plouffe's formula
Starting from here, and with order greater than
1 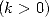 , we have all the bits to link the polylogarithm to the
BBP formulae and now the functions
, we have all the bits to link the polylogarithm to the
BBP formulae and now the functions 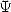 .
.
At this stage, we need to note that the
polylogarithms are of the style 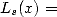
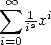 while the BBP formulae
use more series of type
while the BBP formulae
use more series of type 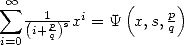 . Intuitively, instead of having the parameter
. Intuitively, instead of having the parameter 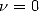 as the equivalence
as the equivalence 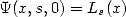 let us see, the polylogarithms
are able to be "developed" by giving a linar relation between the
functions
let us see, the polylogarithms
are able to be "developed" by giving a linar relation between the
functions 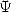 where
where 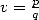 , basicly the BBP formulae. In this
form with the parameters of the function
, basicly the BBP formulae. In this
form with the parameters of the function
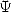 , we can see that this kind of generalisation of the
arctan since we don't have
, we can see that this kind of generalisation of the
arctan since we don't have 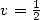 anymore but more generaly
anymore but more generaly
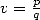 .
.
5.5 The interest of the BBP formulae
This formulation has showed us that we can in
base 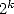 and
and 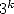 calculate any digits of constants resulting
from this kind of series, without knowing the previous. Why ? I will explain it a bit later on
the page consacred of Plouffe but in an
intuitive way, we can notice that the development in base 10 of a
number
calculate any digits of constants resulting
from this kind of series, without knowing the previous. Why ? I will explain it a bit later on
the page consacred of Plouffe but in an
intuitive way, we can notice that the development in base 10 of a
number 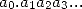 is
is 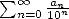 with
with 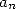 an
integer between 0 and 9. So by considering the series of the kind
an
integer between 0 and 9. So by considering the series of the kind 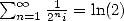 we are not far
from the development in base 2 !
All we need is to calculate the decimals in a certain place of
we are not far
from the development in base 2 !
All we need is to calculate the decimals in a certain place of  .
.
And this is what happened not only with 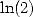 but also with loads of other constants around
but also with loads of other constants around 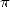 ,
the Riemann function
etc...
,
the Riemann function
etc...
Futhermore, we can notice that they are
rational series and so they are perfect target for simple calculation
of the decimals of Pi. We know more immediatly that thanks to the term 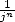 of the series how many decimals we can obtain in practise with n
terms of the series. In fact, with
of the series how many decimals we can obtain in practise with n
terms of the series. In fact, with 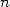 decimales, in that case we obtain
decimales, in that case we obtain 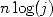 decimales (and even a bit more if we take into account the term in
decimales (and even a bit more if we take into account the term in
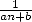 ).
).
Alternating intensive phases of exploration with more calm phases, the search in that direction was very fertile! A few elements in the following paragraphs
In a synthetic way, Gery Huvent put forward a few integrals useful to the decomposition that the previous paragraph talk about. We will present it here, with their application to the research into BBP formulae.This text takes with a few adaptations the article by Gery Huvent [12] which can not be more fundamental!
back to home page