4 Formula of type Machin

Compared to the function 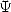, it's the case when it's parameter are 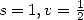, and 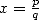varies.

The Arctan function is expressed this way with the function 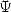. Hence, we get

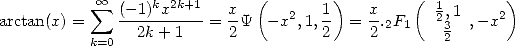(27)

This means that the Arctan formula of type Machin is expressed as a linear combination of the function 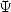. For example, we have according to Euler's formula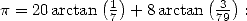

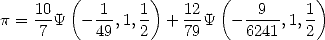(Euler)

Here we are dealing with rational series which made up the principle method to calculate Pi between their "official" discovery by Machin (1705) and those of modern algorithm like Brent-Salamin / Borwein at the end of the 70s.

This formula correspond in hypergeometric notation to the form

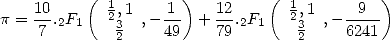(28)

The proof is done by using the formula

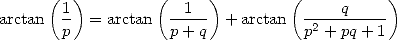(29)

several time. It's long, might as well say it! A simple method was done by the Borwein brother's in 1987, which consist to show that a formula

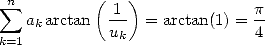(30)

is equivalent to the complex expression

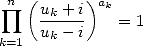(31)

Starting from here, the proof of the arctan formula is as simple as the product of complex number !