|
The world of Pi - V2.57 modif. 13/04/2013 |
|
|
|
The hypergeometric series, harmonic and Pi
2 february 2006
Content Page
1 A small quick historical recap
2 Introduction to hypergeometric series
2.1 Definition
2.2 A few properties and simple examples
3 The Psi function: Basis of formlae of the kind Machin or BBP
3.1 Definition
3.2 Differential equation
4 Formulae of kind Machin
5 Formulae BBP : The technic
5.1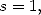
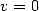 :
The polylogarithms
:
The polylogarithms
5.2 Link between integrals, BBP formulae and polylogarithms
5.3 Integrals and BBP formulae
5.4 Function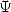 and
polylogarithms
and
polylogarithms
5.5 Interest in BBP formulae
6 BBP formulae in base 2 :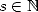 ,
,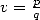 ,
, 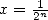 in
in 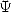
6.1 The considered integrals
6.2 The method
6.3 Formulae for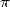 ,
, 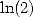 ,
, 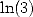 and
and 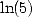
6.4 Case of polylogarithms of order : Formulae of order 2
: Formulae of order 2
6.5 Case of polylogarithms of order 3
6.6 Case of polylogarithms of order 4
6.7 Case of polylogarithms of order 5
7 fixed integers,
fixed integers,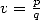 ,
, 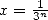 : BBP in base 3
: BBP in base 3
7.1 Formulae for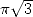
7.2 Formulae of order 2 : Integrals with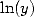
7.3 Formulae of order 3 : Integrals with ln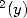
8 And the other bases then ? ?
9 Polygamma and Clausen
9.1 Polygamma functions
9.2 The function digamma
9.3 Polygamma of order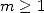
9.4 Combinations of Kölbig
10 Introduction to factorials and combinations
10.1 A first example
10.2 Umbral calculus
11 Central binomial series
11.1 Inversion of combinations
11.2 Useful deveoppements
11.3 First direct formulae
11.4 Formulae of greater order
12 Other binomial coefficients
12.1 Primitive formulae
12.2 Polynomiales factorial formulae
12.3 Then, what does this mean ?
12.4 Proof
12.5 Fast combinations: factorial BBP formulae
12.6 Then, what does this mean ?
12.7 Typical proof
12.8 Product of combinations
13 Harmonic series
13.1 Proximity of harmonic series and of polylogarithms
13.2 Study of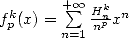 and of
and of
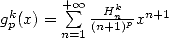
13.3 Applications of the calculations of certain series
13.4 Generalisations
14 Series of greater factorial : Ramanujan, Borwein, Chudnovsky....
14.1 Squared central binomial coefficients : Elliptical formulae
14.2 Cubed central binomial coefficients: Ramanujan's identity
15 Other hypergeometric formulae concerning
References
1 A small quick historical recap
2 Introduction to hypergeometric series
2.1 Definition
2.2 A few properties and simple examples
3 The Psi function: Basis of formlae of the kind Machin or BBP
3.1 Definition
3.2 Differential equation
4 Formulae of kind Machin
5 Formulae BBP : The technic
5.1
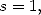
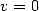 :
The polylogarithms
:
The polylogarithms 5.2 Link between integrals, BBP formulae and polylogarithms
5.3 Integrals and BBP formulae
5.4 Function
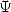 and
polylogarithms
and
polylogarithms 5.5 Interest in BBP formulae
6 BBP formulae in base 2 :
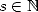 ,
,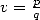 ,
, 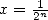 in
in 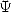
6.1 The considered integrals
6.2 The method
6.3 Formulae for
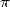 ,
, 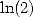 ,
, 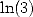 and
and 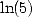
6.4 Case of polylogarithms of order
 : Formulae of order 2
: Formulae of order 2 6.5 Case of polylogarithms of order 3
6.6 Case of polylogarithms of order 4
6.7 Case of polylogarithms of order 5
7
 fixed integers,
fixed integers,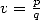 ,
, 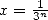 : BBP in base 3
: BBP in base 3 7.1 Formulae for
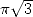
7.2 Formulae of order 2 : Integrals with
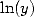
7.3 Formulae of order 3 : Integrals with ln
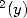
8 And the other bases then ? ?
9 Polygamma and Clausen
9.1 Polygamma functions
9.2 The function digamma
9.3 Polygamma of order
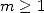
9.4 Combinations of Kölbig
10 Introduction to factorials and combinations
10.1 A first example
10.2 Umbral calculus
11 Central binomial series
11.1 Inversion of combinations
11.2 Useful deveoppements
11.3 First direct formulae
11.4 Formulae of greater order
12 Other binomial coefficients
12.1 Primitive formulae
12.2 Polynomiales factorial formulae
12.3 Then, what does this mean ?
12.4 Proof
12.5 Fast combinations: factorial BBP formulae
12.6 Then, what does this mean ?
12.7 Typical proof
12.8 Product of combinations
13 Harmonic series
13.1 Proximity of harmonic series and of polylogarithms
13.2 Study of
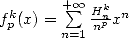 and of
and of
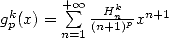
13.3 Applications of the calculations of certain series
13.4 Generalisations
14 Series of greater factorial : Ramanujan, Borwein, Chudnovsky....
14.1 Squared central binomial coefficients : Elliptical formulae
14.2 Cubed central binomial coefficients: Ramanujan's identity
15 Other hypergeometric formulae concerning
References
back to home page
