|
The world of Pi - V2.57 modif. 13/04/2013 |
|
|
|
15 Other
hypergeometric formulae concerning 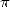
There exist loads of hypergeometric formulae
linked to 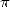 , for example
, for example
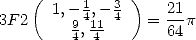 |
(715) |
that I've found, or
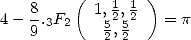 |
(716) |
that I've read. The formulae by Ramanujan or Chudnovsky can equally be written under the form of hypergeometric functions. The problem is to not loose yourself in the coefficients, the hypergeometric formulae have a few too many free parameters! Basicly impossible to find an easy generalisation in all of those this.
Conclusion 27 Of
course, this page is to evolve according to my courage, my last
findings, or even your ideas or contribution! My first objective was to
showw you how a certain form of integral, which is very often
equivalent to a hypergeometric series, can give a familly of constant
that we understand more now: 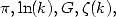 etc...
etc...
This current subject will without doubt be
more clear and unified in the following years. It doesn't have to be
that hard (at least how I presented it! ) but this does show some
really promosing leads, numerous and sometime a bit forgotten by our
dear mathematicians!
back to home page
