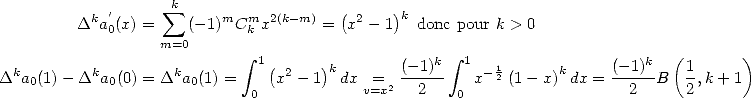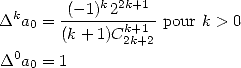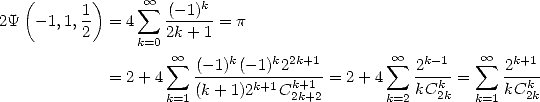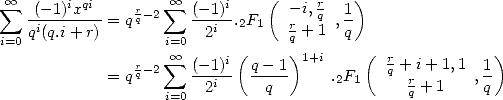|
The world of Pi - V2.57 modif. 13/04/2013 |
|
|
|
10 Introduction to factorials and combinations
What is very interesting, is that we will
always be able to observe the same kind of constant even with the
introduction of an equivalent combination or factorial (as long as we
stay in a 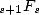 ), this is why
), this is why 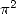 and the logarithms will represent the essential results given by simple
hypergeometric. On the other hand, as soon as we introduce a squared
combination for example, we will obtain different kind, something to do
with the gamma function most of the time (and so is
and the logarithms will represent the essential results given by simple
hypergeometric. On the other hand, as soon as we introduce a squared
combination for example, we will obtain different kind, something to do
with the gamma function most of the time (and so is 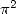 ! but of a less obvious way).
! but of a less obvious way).
10.1 A first example
The introduction of the combination is justified by several very similar series with or without the presence of combinations. For example,
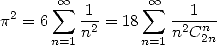 |
(Euler) |
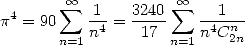 |
(Comtet 1974) |
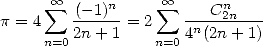 |
(362) |
Which means that in fact as soon as we find a result to this function, we have a little hope to find the same kind of result with a combinations with a central binomial coefficient for example. It's simply due to the form quite close to generators functions of those series (1211).
10.2 Umbral calculus
We can establish a link betweens the series
with combinations (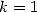 more precisely) and the series without (
more precisely) and the series without (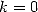 )
with the help of the acceleration of the convergence by Euler's method.
This is a particular case of the formula for "finite differences" which
is the discrete version of Taylor's expansion (
)
with the help of the acceleration of the convergence by Euler's method.
This is a particular case of the formula for "finite differences" which
is the discrete version of Taylor's expansion (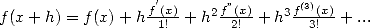 ). It's the theory known under the name of ”Umbral
calculus”, whose origines goes back to Sylvester (1814-1897). The
acceleration method by Euler consist to replacing the sum of a serie by
the sum of the difference in terms of the serie.
). It's the theory known under the name of ”Umbral
calculus”, whose origines goes back to Sylvester (1814-1897). The
acceleration method by Euler consist to replacing the sum of a serie by
the sum of the difference in terms of the serie.
More precisely, we choose an alternating serie
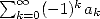 and we calculate the finite
difference of order
and we calculate the finite
difference of order 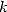 for
for 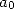 :
:
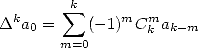 |
(363) |
then
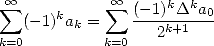 |
(364) |
The trick, it's that the first term is sometime written as combinations or factorial ratio and other symbols of Pochammer ! Application :
We know that 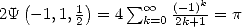 . Hence we have
. Hence we have 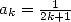 .
.
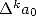 being quite delicate to calculate directly, we let the
function
being quite delicate to calculate directly, we let the
function
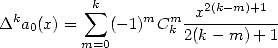 |
(365) |
We are going to look for the value in 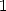 of
course. And we calculate it !
of
course. And we calculate it !
where 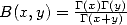 is the complete
Bêta function which is worth in this case
is the complete
Bêta function which is worth in this case 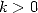 integers
integers
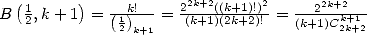 (interesting...).
(interesting...).
From which we obtain
and hence according to the formula 364
Unfortunatly, I have not found how to generalise this method... However, we have still the more general formula
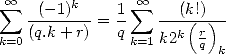 |
(369) |
or even
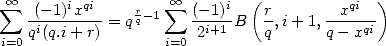 |
(370) |
where B is an incomplete Bêta , if I'm not mistaken...
Similarly, by using the link between the incomplete bêta and the hypergeometric
where 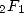 is the hypergeometric function.
is the hypergeometric function.
Basicly, the introduction to factorials can be interesting, very interesting....
back to home page